Paul Tseng

C-344 Padelford Hall
Department of Mathematics, Box 354350
University of Washington
Seattle, WA 98195-4350
Tel: (206) 543-1177
Fax: (206) 543-0397
Email: my last name@math.washington.edu (trying to avoid spam)

Background: I received my B.Sc. from Queens University (Canada) in 1981 and my Ph.D. from Massachusetts Institute of Technology (U.S.A.) in 1986. After spending one year at the University of British Columbia and three years at Massachusetts Institute of Technology, I came to the University of Washington in 1990. My research area is mainly in continuous optimization, with side interests in discrete optimization, distributed computation, network and graph algorithms. My free-time interests include drawing/painting, various sports, and traveling (preferrably by bicycle or kayak) to anywhere in the world. Here are photos from my bicycling trips, 1986-2000 , kayaking trips, 2001 on the Danube and elsewhere, kayaking trip, 2002 on the Mekong, bicycling trip, 2003 along the Baltic shores, backpacking trip, 2004 in Kenya, kayaking trips, 2005 on the Nile, Red Sea, and Vancouver Island, kayaking trips, 2006 on the Danube and Yellow River, China, kayaking trips, 2008 on the Rio Madre de Dios, Peru, a headwater tributary of the Amazon river.

Web Philosophy: Minimalism.

Research

  • My Recent Research Papers
  • Fortran relaxation codes for nonlinear cost generalized network flow (updated on March 2005)
  • Fortran auction and relaxation codes for assignment/shortest path/linear cost network flow
  • Matlab code of coordinate gradient descent (CGD) method for unconstrained optimization with l1-regularization (updated on December 2007)
  • Applications in Signal Denoising
  • Applications in Protein Folding
  • Optimization Seminar
  • West Coast Optimization Meeting, Spring edition (the next one is May 2, 2009)
  • Upcoming conf./workshops: OPTIMA09 (March 25-27 2009) , SPARS09 (April 6-9 2009) , ISMP (August 23-28 2009) , Combinatorial Optimization at Work (Sept 21--Oct 9 2009)

    Recent Talks

  • ICNONLA 2009 talk, Lijiang, August 2009 (ESDP and SDP Relaxation of Sensor Network Localization)
  • OptimA talk, Univ. Illinois, March 2009 (Large-Scale Convex Optimization over Matrices for Multi-task Learning)
  • South California Optimization Day talk, San Diego, March 2009 (ESDP and SDP Relaxation of Sensor Network Localization)
  • IASI seminar talk, Rome, September 2008 (On ESDP and SDP Relaxation of Sensor Network Localization)
  • SIMAI minisymposium talk, Rome, September 2008 (Gradient Methods for Sparse Optimization with Nonsmooth Regularization)
  • MOPTA talk, August 2008 (Accelerated Proximal Gradient Methods for Convex Optimization)
  • Kyungpook National University seminar talk, February 2008
  • The Chinese University of Hong Kong seminar talk, February 2008 (On ESDP Relaxation of Sensor Network Localization)
  • Hong Kong Polytechnic Univ. seminar talk, February 2008 (Block-Coordinatewise Methods for Sparse Optimization with Nonsmooth Regularization)
  • INFORMS talk, November 2007 (Parametrized Variational Inequality Approaches to the Generalized Nash Equilibrium Problem)
  • WCOM, Kelowna talk, October 2007 (From Evolutionary Biology to Interior-Point Methods)
  • ICCOPT 2007 talk, August 2007 (Coordinatewise Distributed Methods for Large Scale Convex Optimization)
  • UBC CS seminar talk, April 2007 (Gauss-Seidel for Constrained Nonsmooth Optimization and Applications)
  • Banff BIRS workshop talk, Nov 2006 (pOCP relaxation of sensor network localization)
  • Taiwan Normal University workshop talk, March 2006 (Optimization methods with signal denoising applications)
  • Univ. Vienna talk, June 2006 (SOCP relaxation of sensor network localization)
  • talk at MIT, March 2006 (SDP relaxation of quadratic optimization with few homogeneous quadratic constraints)
  • SIOPT talk at Stockholm, May 2005 (Smoothing methods for second-order cone programs/complementarity problems)

    Teaching

  • Math 582B (Winter 2009)
  • Math 409 (Spring 2009)
  • Math 516 (Spring 2009)

    Math Quotes

  • The UW Math Club is alive and well. Visit its new webpage for the latest happenings.

    PhD Associates

  • Jein-Shan Chen (2004), Sangwoon Yun (2007) Ting Kei Pong (200?)
  • Job opportunities in optimization

    Other sites

  • MathAcrossCampus
  • Math Programming Society
  • Institute for Operations Research and Management Sciences
  • American Mathematical Society
  • Optimization Technology Center at Argonne National Laboratory
  • Terry Rockafellar's home page
  • Al Goldstein's free classical music archive
  • A list of fun math sites from San Francisco Exploratorium

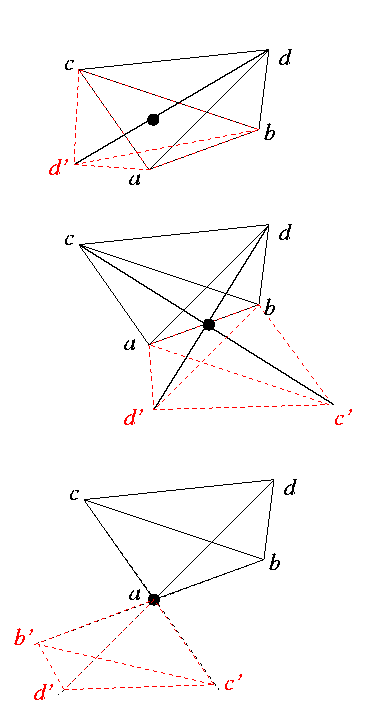
    A Simplex method:
    In a simplex method of Nelder-Mead type, a simplex is reflected with respect to a point on its boundary. The top figure shows the reflected simplex (drawn in red dashed line) when the point (the black dot) is the centroid of three vertices a, b, c. The middle figure shows the reflected simplex when the point is the centroid of two vertices a, b. The bottom figure shows the reflected simplex when the point is the vertex a.