Projects

Ocean Modeling | Computational Fluid Dynamics | Numerical Linear Algebra | Stochastic Modeling | Machine Learning

An Adaptive Locally Nonhydrostatic Ocean Model

Designed a novel ocean model that locally resolves complex dynamics and achieves computational savings compared to traditional globally-non-hydrostatic models. Currently incorporating this model into a C++ hybridizable Discontinuous Galerkin solver and devising numerical techniques to overcome computational limitations and conduct large-scale regional ocean simulations.

Saravanakumar et al. To be sumbitted to Ocean Modeling (2025)

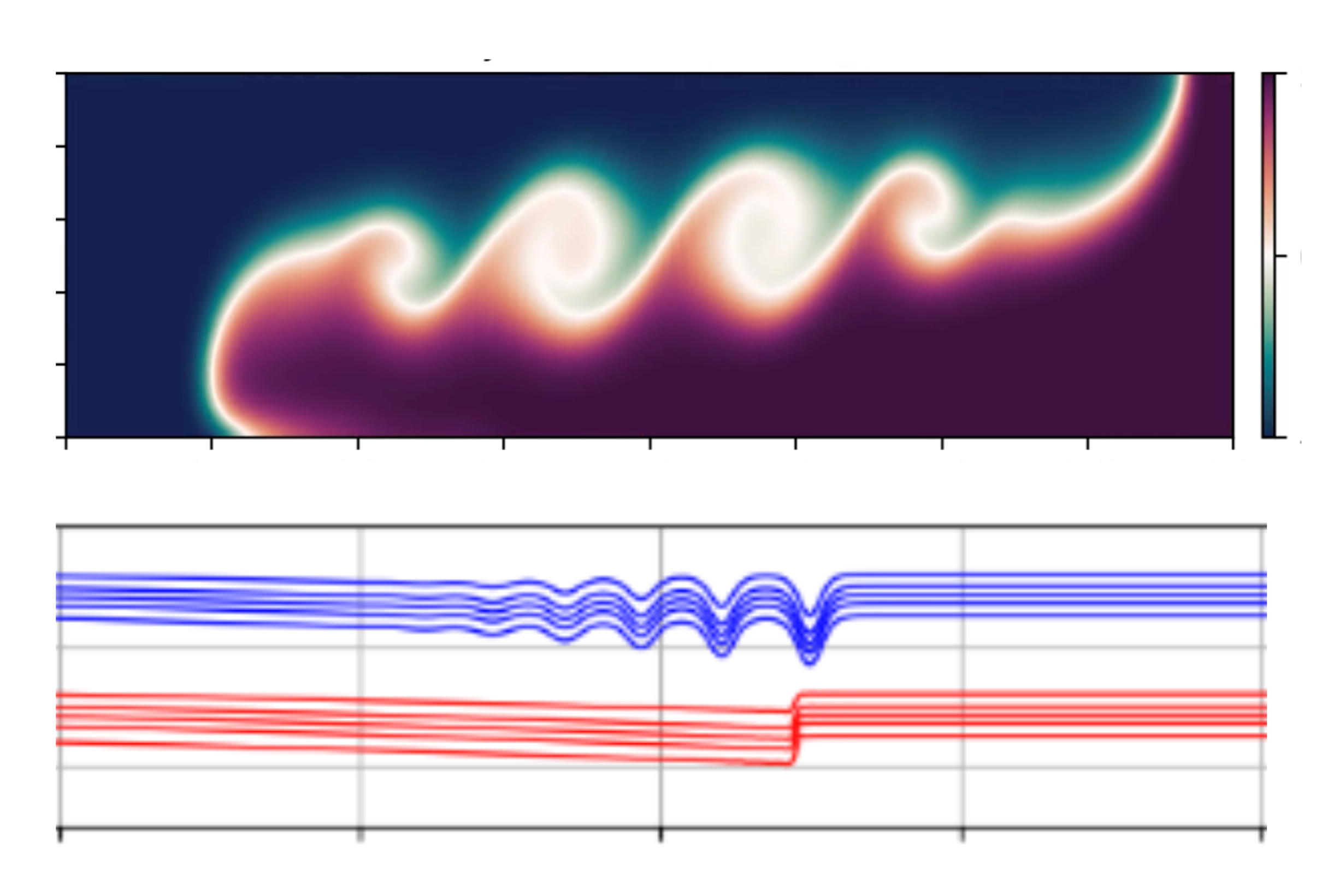
Flapping Dynamics of Multi-layered Plates

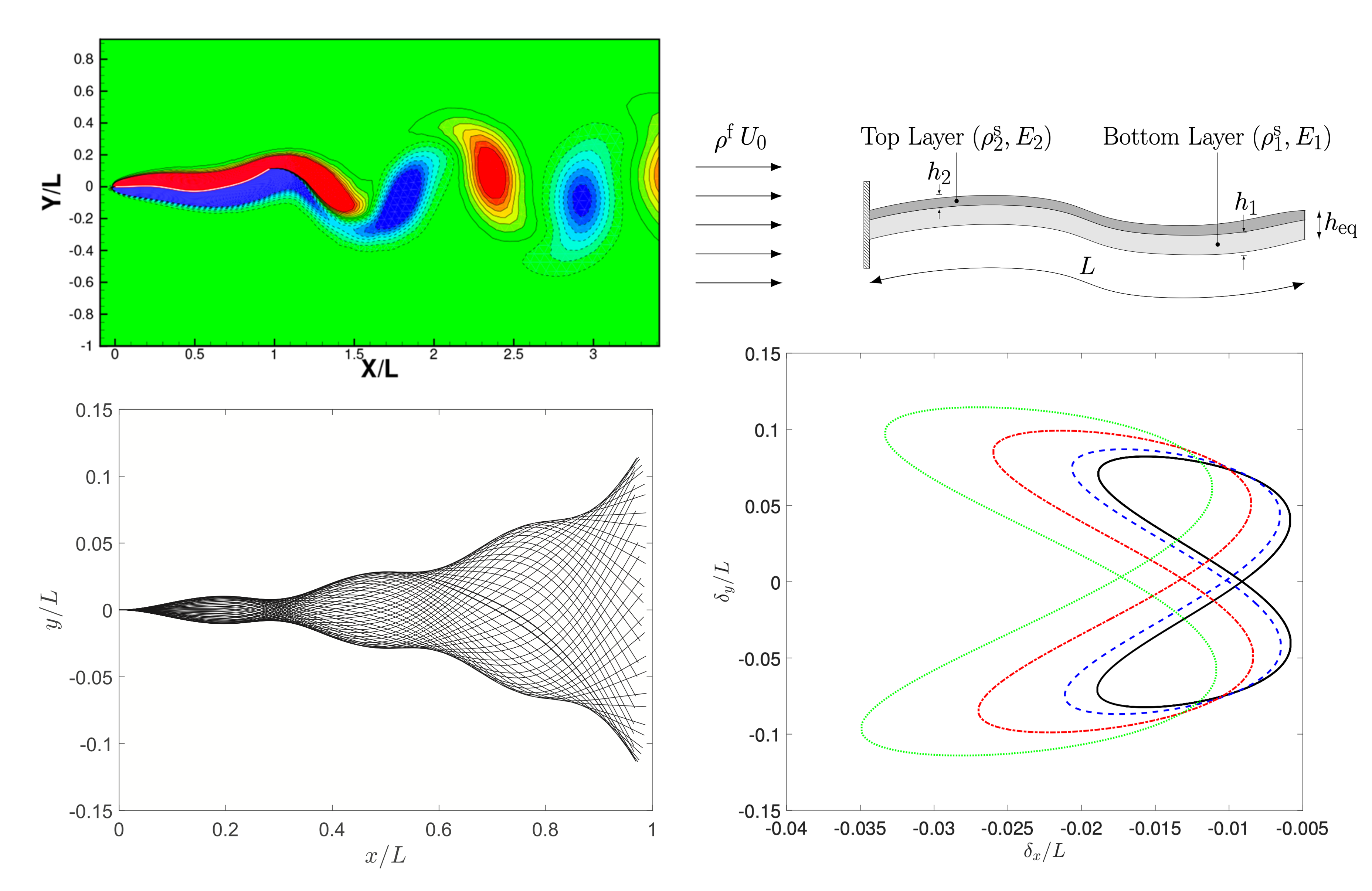
Piezoelectric patches mounted on flexible plates exhibiting flapping motion are used to generate energy. These patches are typically multilayered but studies have been primarily restricted to the flapping dynamics of single-layered plates. Employed a MATLAB-based finite element method code to study fluid structure interaction dynamics of realistic multi-layered plates flapping in a uniform flow. Numerical investigations new revealed response regimes due to the anisotropy within the plate. Enhanced solver to allow coupling between high-order fluid elements and low-order structural elements to improve computational efficiency.

Saravanakumar et al. Physics of Fluids (2021) [link]

Extension of High-Order Rarefied Gas Dynamics Solver

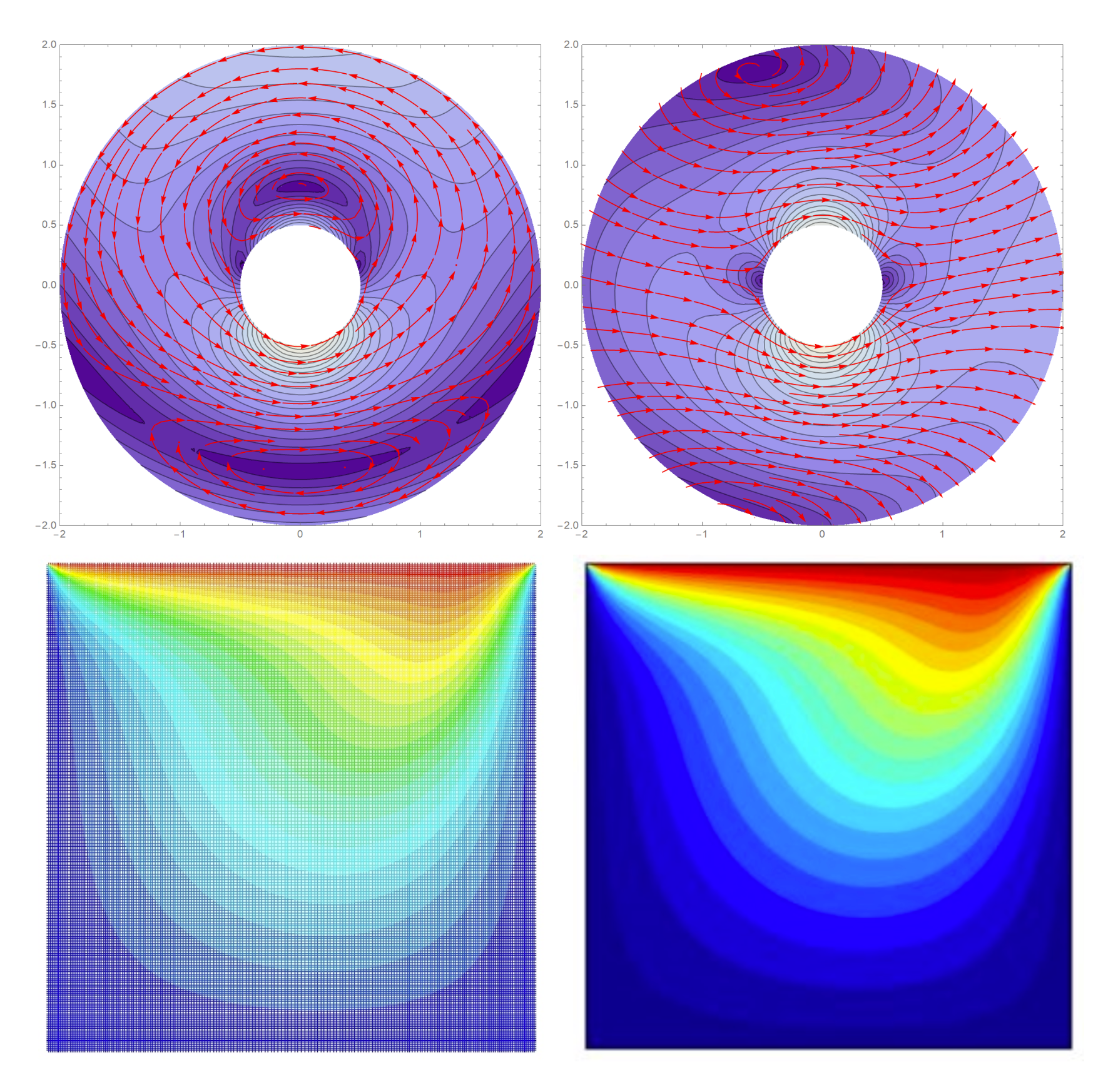
The regularized 13 moment (R13) equations are a macroscopic model for the description of rarefied gas flows in the transition regime. Extended a finite element solver for the R13 equations FenicsR13 to accommodated non-linear conservation equations. Compared solutions with that produced by commerical software ANSYS and COMSOL for the case of non-isothermal lid-driven cavity flow. Investigated the solver’s CIP stabilization scheme to deduce optimal stabilization parameters.

Saravanakumar, A. K. Bachelor Thesis (2021) [Report]

Detatched Eddy Simulation of Turbulent Flow Past Structures

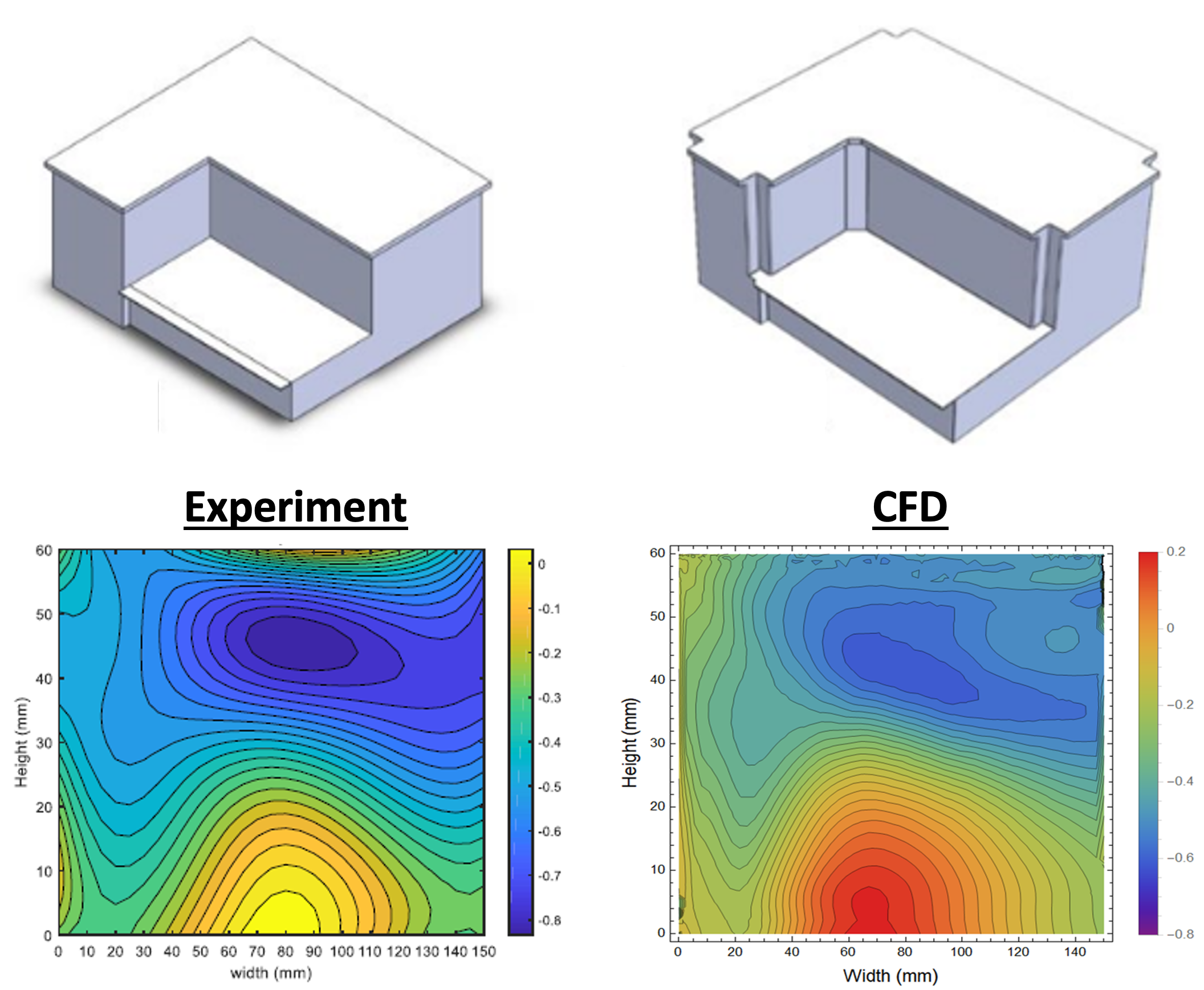
Optimized building design for the LIGO India observatory to minimize wind load and vibrations by incorporating edge modifications and windbreaks. Turbulent flow past the building was simulated using the 3D Detatched Eddy Simulation (DES) framework in ANSYS Fluent, leveraging LES for near-field and RANS far-field. The CFD results were validated against wind tunnel experiments on a scaled model with good correlation in pressure coefficients and vibration response.

Vishwanath, N., Saravanakumar A.K., et al. Wind and Structures (2022) [link]

Multigrid Finite Element Schemes

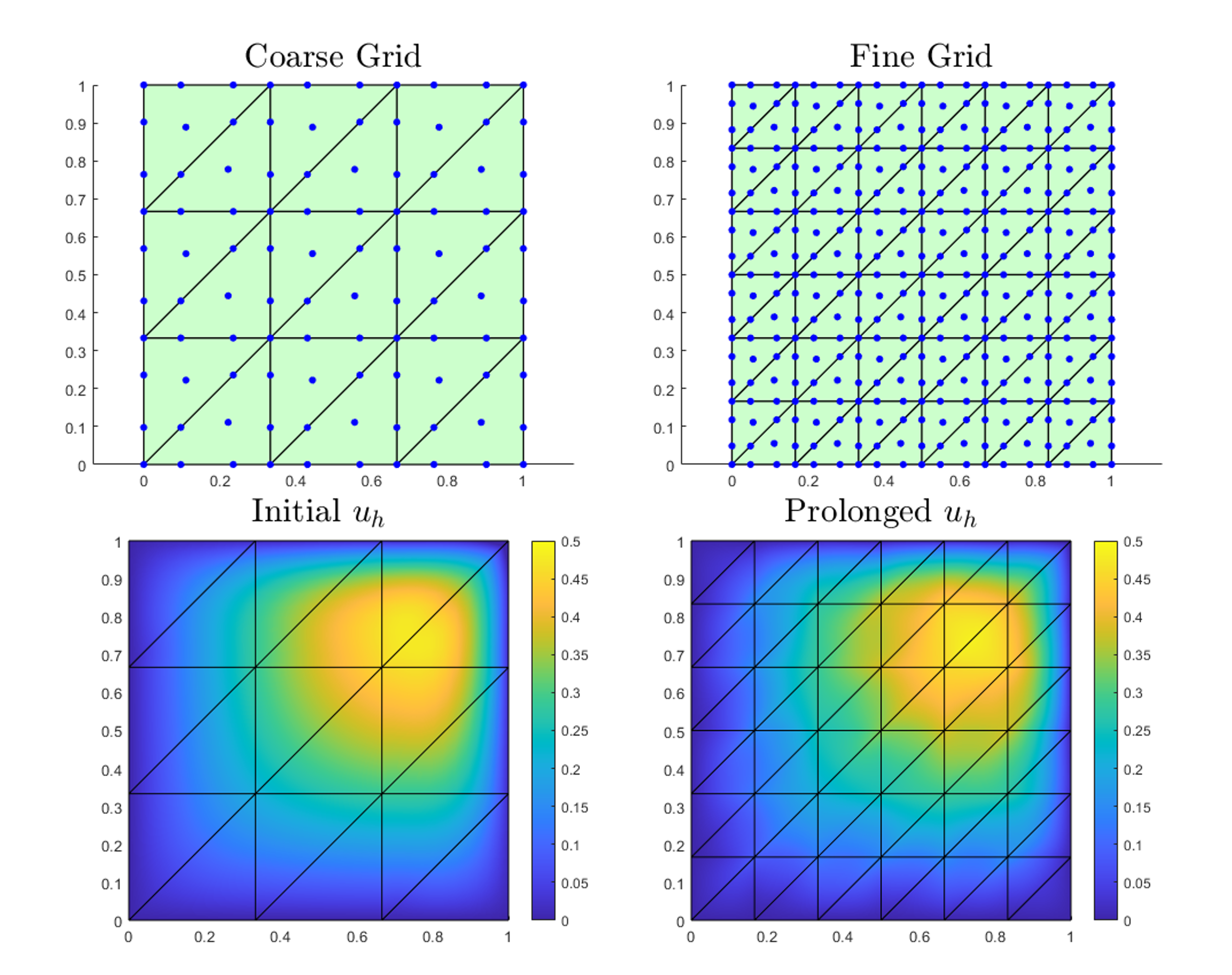
Multigrid methods offer the exciting prospect of solving certain PDEs with computation and memory proportional to the number of unknowns O(n). Implemented multigrid methods in MATLAB to solve linear systems arising from discontinuous Galerkin finite element discretizations of elliptic PDEs. Achieved nearly mesh size independent performance while solving a set of manufactured solutions to Poisson problems.

MIT 18.335 [Report] | MIT 16.930 [Slides]

Magnetohydrodynamic Simulation of Flow through Linear Induction Pumps

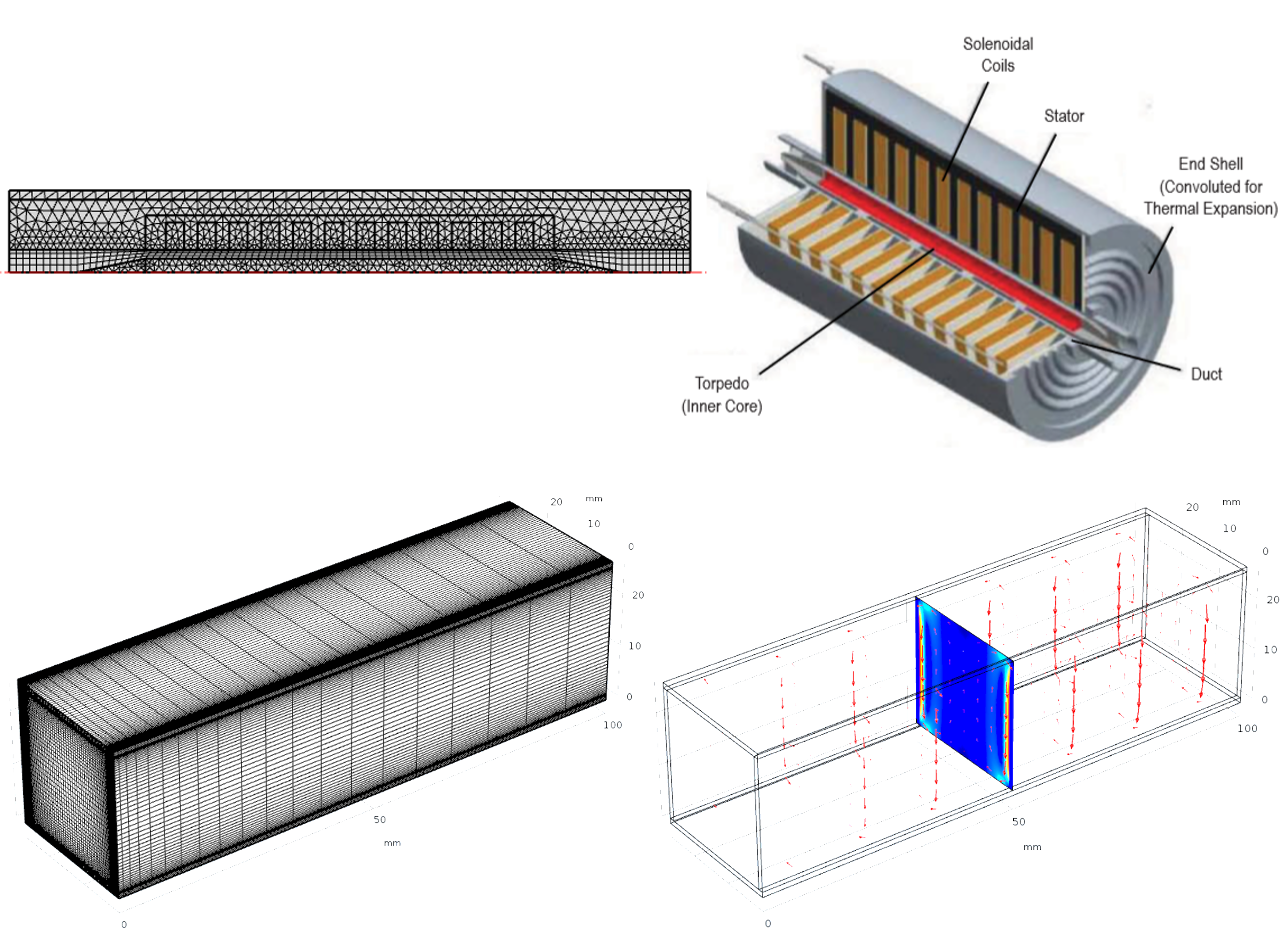
Electromagnetic pumps used to cool fast reactors work by moving liquid metal using electromagnetic induction. I worked towards magnetohydrodynamic (MHD) simulations of liquid sodium flow through annular linear induction pumps (ALIP). Validated COMOSOL-based MHD simulations of laminar flow of conducting liquid in a rectangular duct under a uniform magnetic field against benchmark solutions (Hunt et al. 1965 JFM). Conducted preliminary simulations of liquid sodium flow through an ALIP using the MHD framework.

Reinforcement Learning for Preconditioner Discovery

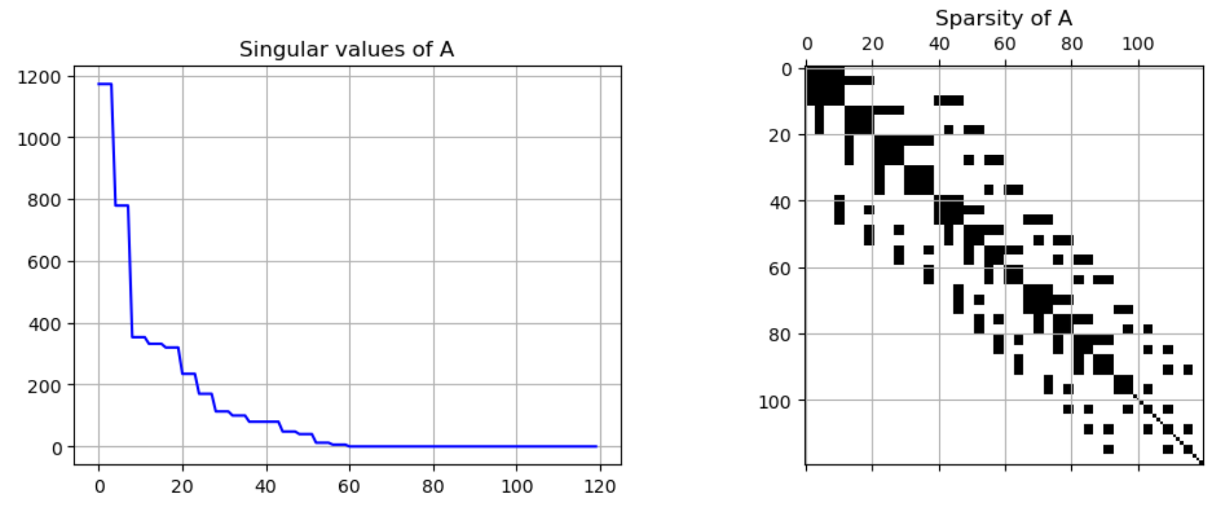
Preconditioning linear systems arising from numerical discretization of PDEs is a crucial for robust simulations. Developed a reinforcement learning framework in Python using the Advantage Actor Critic and Proximal Policy Optimization models to generate preconditioners for finite element discretized elliptic PDEs. ON GOING PROJECT

MIT 6.7920 [Report] [Repo]

Upwinded Transformer for Advective Flows

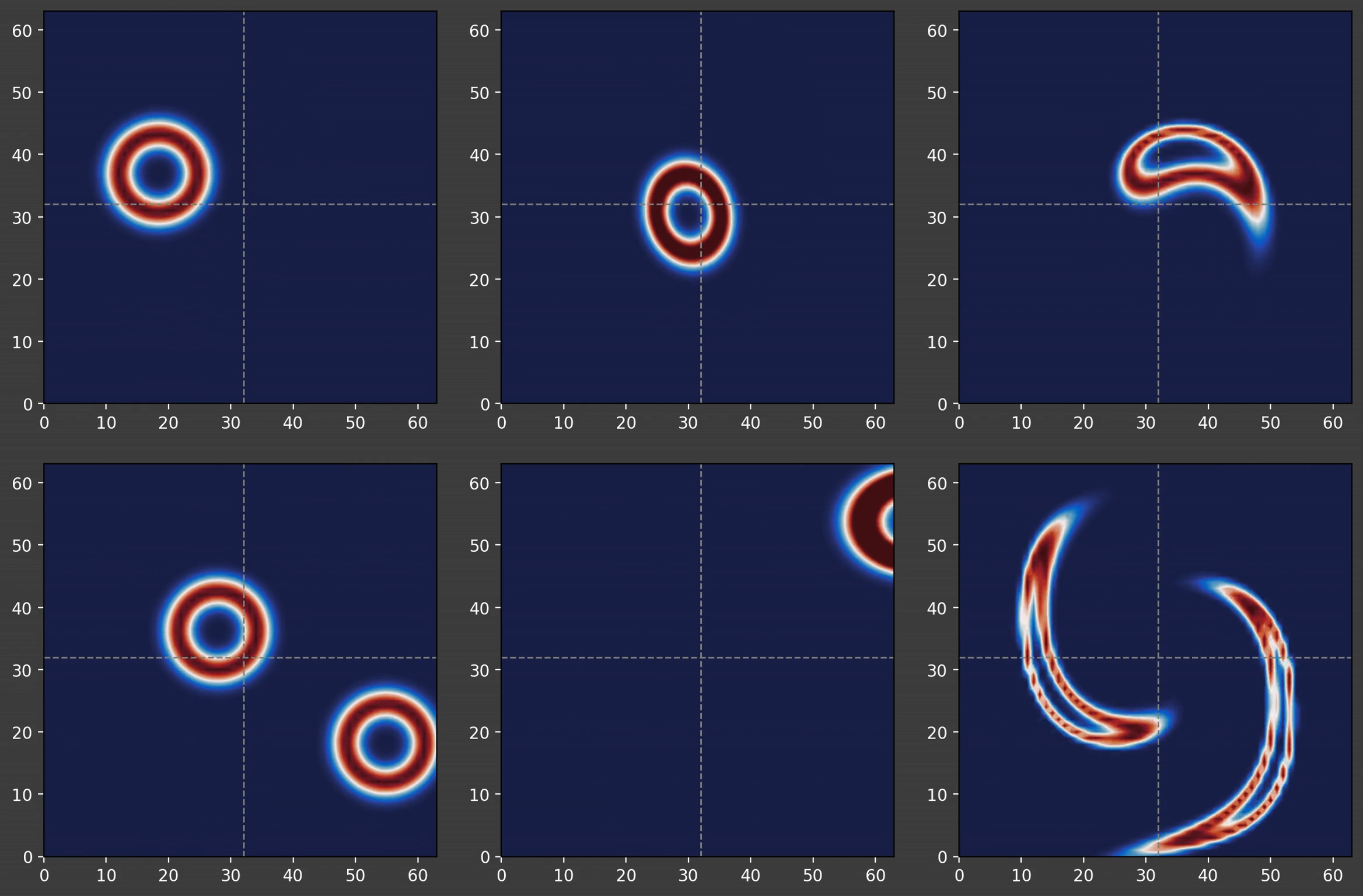
Developed a transformer-based neural network architecture on PyTorch to predict temporal evolution of tracer fields in external flow fields. ON GOING PROJECT

MIT 6.7990 [Report] [Repo]

Multilevel Monte Carlo Methods

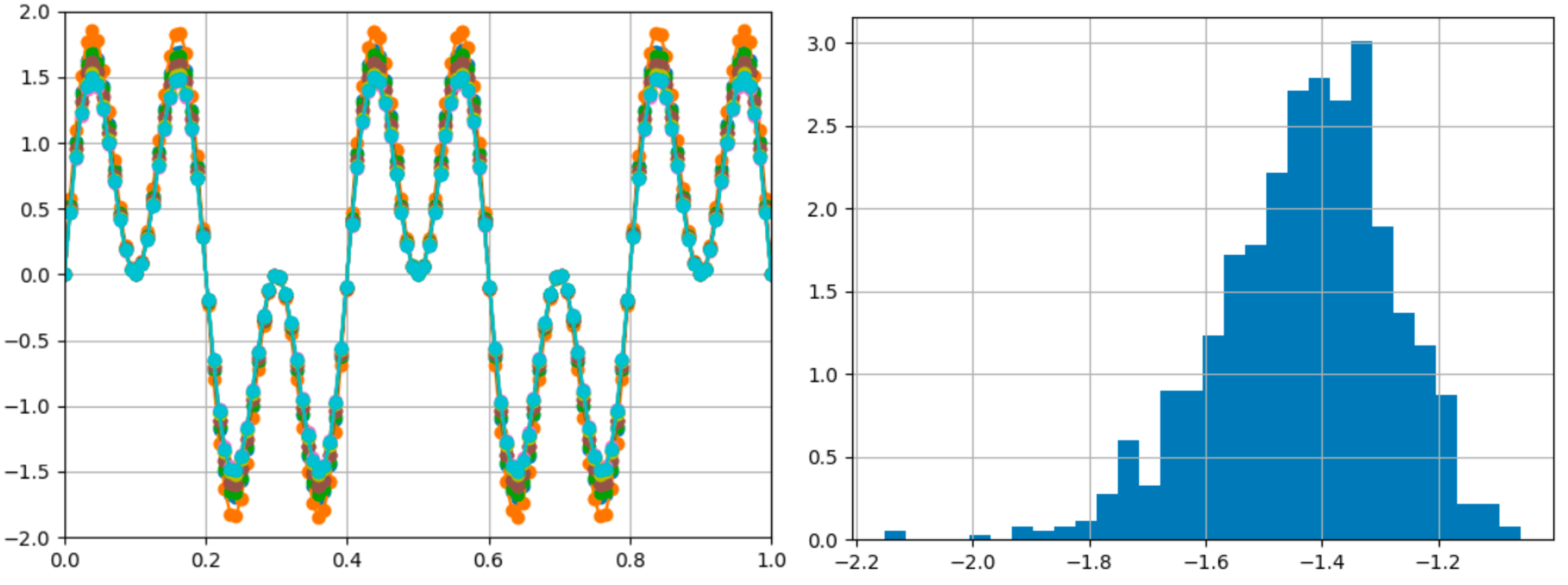
Multilevel Monte Carlo (MLMC) methods are hierarchical variance reduction methods widely used to reduce the computational cost of standard Monte Carlo. Implemented MLMC in Python using a finite element solver for the Poisson problems. Conducted numerical experiments to empirically verify the analytical optimal variance reduction and sample ratio.

MIT 16.940 [Report]