Research Focus
Fundamental signal processing theory
A fundamental question in statistical signal processing, that arises in applications as diverse as radar, sonar, wireless communications and econometrics is: Given finite number of samples, can one reliably discriminate signal from noise?
My research answers this in an application independent sense. We show that if the SNR is above a threshold which is a simple function of the number of sensors (or dimensionality of the system) and the number of signal-plus-noise and noise-only samples then reliable detection is possible in an optimal manner using a new random matrix theory inspired algorithm we have developed. Below this SNR threshold, reliable detection is (asymptotically) just not possible.
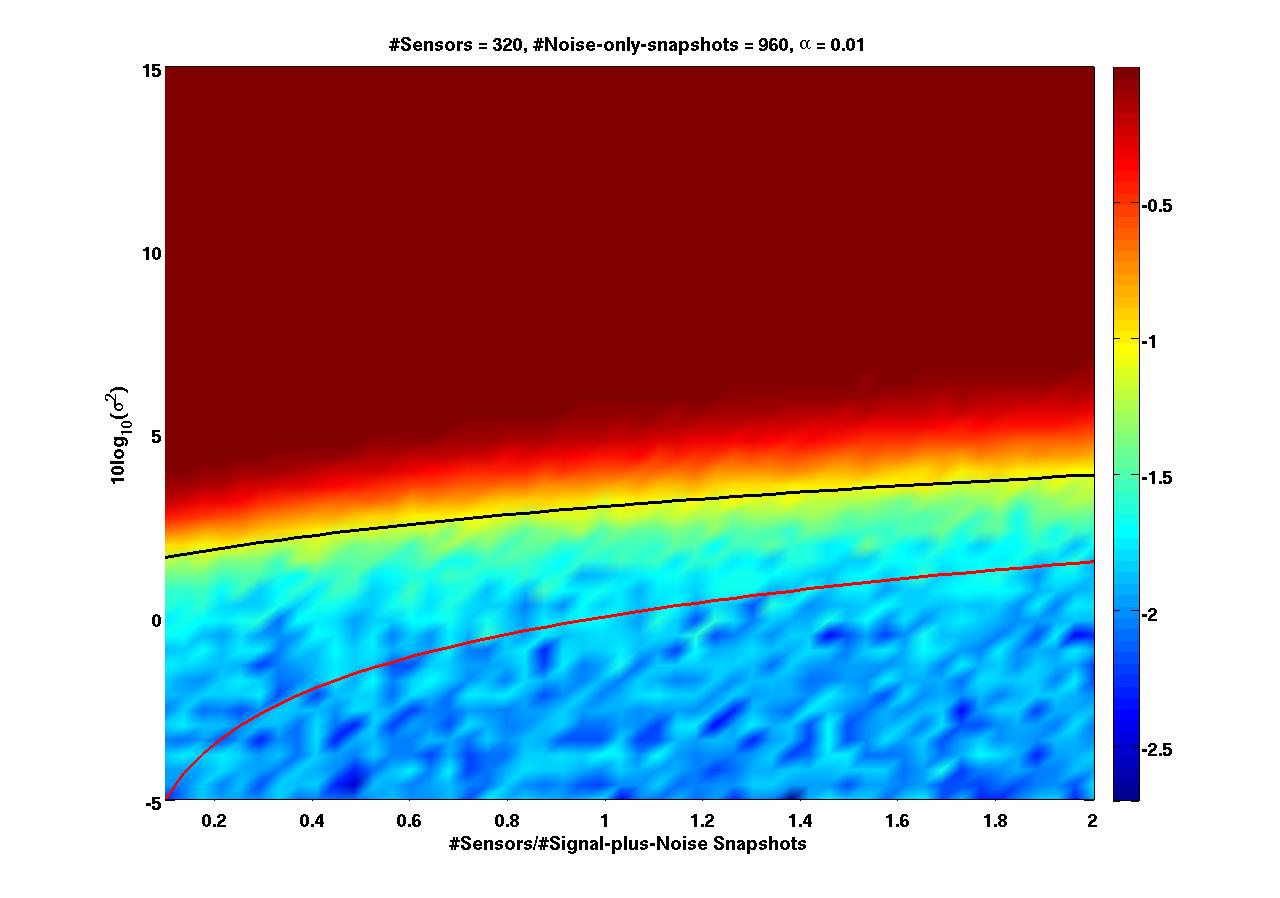
The figure above illustrates this "hot zone/cold zone" behavior in signal detection by plotting the logarithm of the probability of accurate detection. The superimposed black line is the predicted SNR threshold for this example when both the noise-only covariance matrix and the signal-plus-noise covariance matrix are estimated using finite samples. The superimposed red line is the predicted SNR threshold if the noise covariance were known perfectly. For additional details see the sequence of papers downloadable here and here.
Preliminary results show that this predicted threshold is remarkable accurate in real-world settings. We have been using sensor array data graciously provided by the Laboratory for Autonomous Marine Sensing Systems.Adaptive signal processing for communications
A major challenge while communicating in dynamic channels, such as the underwater acoustic channel, is the large amount of time-varying inter-symbol interference (ISI) due to multipath. In many realistic channels, the fluctuations between different taps of the sampled channel impulse response are correlated. Traditional least-squares algorithms used for adapting channel equalizers do not exploit this correlation structure.
My research addresses this by designing a channel subspace post-filtering algorithm that treats the least-squares channel estimate as a noisy time series and exploits the channel correlation structure to reduce the channel estimation error. Consequently, the performance of the channel estmated based decision feedback equalizer (DFE) is improved as well. We bring into the sharp focus how our algorithm exploits the channel correlation structure and demonstrate its implemntability.
We have tested this algorithm on undersea acoustic communication data collected during experimental trials and have realized a 5-7 dB improvement in performance of a channel estimate-based decision feedback equalizer that uses this post-filtered channel estimate to determine the equalizer coefficients. For additional details see the paper downloadable here.
High-dimensional statistical signal processing
Classical "optimal" multivariate statistical signal processing algorithms for detection and estimation are no longer optimal in modern settings where the dimensionality of the system is large (due to a large number of sensors) and the number of observations available to make inference is relatively small. Classical algorithms will perform poorly or provide faulty inference in such scenarios.
My research focuses on designing implementable detection and estimation algorithms that are robust to high-dimensionality and the finite sample effects. We take our inspiration from random matrix theory.
One example of this is the design of an algorithm that can deblur the sample eigenspectrum from limited observations. For details see the paper downloadable here.
Computational random matrix theory
Sample covariance matrices are ubiquitous in statistical signal processing theory. Random matrix theory is the natural language for understanding the properties of sample covariance matrices.
My research provides, for the first time ever, a concrete computational framework so that the power of random matrix theory can be fully harnessed. Before this work, one could only work with simple examples. Now, arbitrarily complicated examples are amenable.
The development of a random matrix calculator, depicted above, is the culmination of this line of research. The software package RMTool is a MATLAB based package. The underlying theory was developed in the paper downloadable here. For an application to computing the Shannon capacity of a large class of MIMO wireless channels, click here.
Design paradigms from random matrix theory
There are a whole new set of distributions arising from random matrix theory that are becoming increasingly important and starting show up in a lot of different (apparently) unconnected areas such as number theory, bus spacings in Cuernevaca, growth processes, quantum chaos, among others.
My research focuses on whether the associated (as yet unknown) entropy-like optimality criterion associated with these distributions can be exploited for engineering problems?

The figure above, taken from Brian Hayes' article shows samples of several particle location (or level) distributions, some of them mathematically defined and others derived from measurements or observations. All of the samples have been scaled so that exactly 100 levels fit in the space allotted. Thus the mean distance between levels is the same in all cases, but the patterns are nonetheless quite diverse. For example, the earthquake series is highly clustered, which surely reflects some geophysical mechanism. The lower-frequency fluctuations of tree-ring data probably have both biological and climatological causes.
What is special about the random eigenvalue series is that they are rather regularly spaced, though still random. The ubiquity of this distribution in physical systems raises the intriguing prospect of whether mimicing these distributions in some problems could somehow be beneficial? We have some clues and some initial applications. More will surely follow.
For a fascinating account of the ubiquity of the random matrix eigenvalue level distributions (fifth from left in above figure) in physical systems see Percy Deift's paper and Brian Hayes' engaging exposition.