Two broker case: price competition and warfare

To explore some effects of price competition, we begin by considering a simple two-broker system with a single information category. We assume that brokers and consumers are fully knowledgeable about the state of the system (in particular, they know the prices and interest vectors of all of the brokers). Furthermore, they instantly adjust their desired subscription vectors and to maximize their utility given the current set of prices and interest vectors. This last assumption removes the degrees of freedom associated with the subscription matrix by expressing it in terms of the other state parameters (prices and interest vectors) -- a tremendous simplification.

We assume that the brokers update their prices asynchronously. One plausible strategy is for a broker to set its price to the value that maximizes its profit, assuming all other prices remain fixed. Such an update strategy is guaranteed to produce the optimal profit up until the moment when the next broker updates its parameters. We call such a strategy ``myopically optimal'', or myoptimal.

A useful construct for understanding the resulting dynamics is the profit landscape. We define a broker's profit landscape as its utility (given in Eq. 2) as a function of the prices offered by all brokers in the system, itself included. A contour map of the profit landscape for broker 1 in a system with , V=1, and a uniform distribution of consumer interests is shown in Fig. 3a.

  
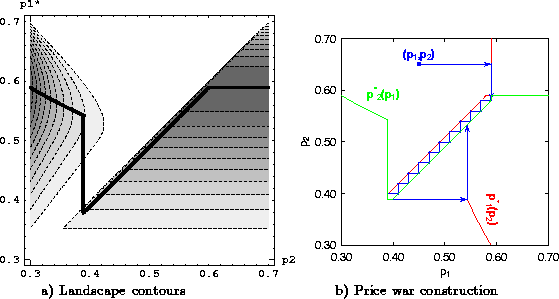
Figure 3: a) Contour map of profit landscape for broker 1 for , with overlaid optimal price function . Profit is higher in dark regions. b) Graphical construction of price-war time series, using functions and .

The landscape shown in Fig. 3a has two distinct humps. The ``cheap'' hump on the right corresponds to the case where broker 1 is cheaper ( ). Here, its profit is completely independent of , and it can charge the monopolistic price derived previously. The ``expensive'' hump on the left corresponds to the case in which broker 1 is more expensive than broker 2, but still able to find customers. This comes about when broker 2 is charging so little that it cannot afford to keep marginal customers -- i.e., customers with low interest levels -- as subscribers. (Recall from the discussion of the single-broker case that a broker will veto a subscription from an insufficiently interested prospective customer.) For these marginal customers, the only alternative is to subscribe to broker 1. In other words, broker 2's rejects constitute broker 1's market.

If broker 1 is myoptimal, it can derive from its profit landscape a function that gives the value of that maximizes the profit when broker 2 charges price . This function is represented as a heavy solid line in Fig. 3a. For , is given by the solution to a cubic equation involving cube roots of square roots of ; in this region it looks fairly linear. The ``vertical'' segment at is a discontinuity as the optimal price jumps from the ``expensive'' hump to the ``cheap'' hump. When , , where is a price quantum -- the minimal amount by which one price can exceed another. For , , the monopolistic price.

If broker 2 also uses a myoptimal strategy, then by symmetry its landscape and price-setting function are identical under an interchange of and . Then the evolution of both and can be obtained simply by alternate application of the two price optimization functions: broker 1 sets its price , then broker 2 sets its price , and so forth. The time series may be traced graphically on a plot of both and together, as shown in Fig. 3b. Assume any initial price vector , and suppose broker 1 is the first to move. Then the graphical construction starts by holding constant while moving horizontally to the curve for . Then, is held constant while moving vertically to the curve . Alternate horizontal moves to and vertical moves to always lead to a price war during which the brokers successively undercut each other, corresponding to zig-zagging between the diagonal segments of the curves. Eventually, the price gets driven down to 0.389, at which point the undercut broker (say broker 1) opts out of the price war, switching to the expensive hump in its profit landscape by setting . This breaks the price war, but unfortunately it triggers a new one. The brokers are caught in a never-ending, disastrous limit cycle of price wars punctuated by abrupt resets, during which their time-averaged utility is half what they expected, and less than half of the monopolistic value.