Given that effective monopolies can occur even
in multi-broker systems, it is useful and instructive
to establish a few simple results
for systems with a single broker.
First, suppose the broker offers a single category,
and that the number of consumers is arbitrarily large,
i.e. B=1, J=1, and 
.
The broker tries to maximize its utility
by choosing a set of
preferred consumers (those c for which 
),
setting a price P, and setting its interest level 
.
The consumers try to maximize their utility simply by
declaring whether they wish to subscribe
to the broker (in which case 
).
Analysis of Eqs. 1 and 2
shows that, for a wide range of parameters,
the equilibrium state is
).
The subscription matrix element 
, which defines
whether or not consumer c has subscribed to the broker,
is the product of two step functions, which can be understood
intuitively as follows.
The first step function, 
,
represents the veto power of the broker: it only wishes
to serve consumers that are interested enough (and the
price is high enough) so that
the expected revenue from an article will exceed the
cost of sending it. The second step function,
, represents the
consumer's veto power: it only wishes to subscribe
to the broker if it is interested enough (and the price
is low enough) so that the expected net benefit of receiving
an article exceeds the cost of processing it.
The monopolistic equilibrium
price 
is constrained by the step functions and the
restriction 
to be
in the range 
;
its exact value depends in detail upon 
, 
, V, and
the distribution of consumer interest probabilities 
in the population. For example, when 
is a uniform distribution, is the solution to a
cubic equation involving , , and V.
Now suppose that the number of categories J
offered by the broker is arbitrary [10].
Assuming that the category
prevalences are all equal ( 
) and the
distribution of consumer interests within a given
category is given by ,
one can derive analytic expressions for the
monopolistic equilibrium price as a function of the
number of categories. Substituting this function
back into Eq. 2, one can derive
the broker's optimal utility as a function of the number
of categories, and then from this the optimal number of
categories. Illustrative results for two very different distributions
are shown in Fig. 2.
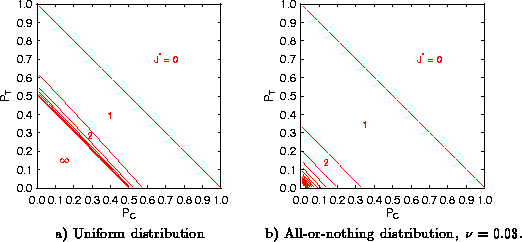
Figure 2: The optimal number of categories 
for the broker
to offer as a function of and (with V=1). a)
is a uniform distribution in the interval (0,1), so 
.
b) is an all-or-nothing distribution:
with probability 
, else 
.
For a wide class of distributions, three behavioral
regimes are observed.
When the combined cost of transport and processing is sufficiently
high ( 
), the optimal number of categories is 0.
In this ``dead'' regime, an article costs more to send and process
than it is worth, even if the consumer is guaranteed to be
interested in it, and so no articles will
be bought or sold. At the other extreme, when the costs are
sufficiently low ( 
, where 
is the
mean of the distribution ), the broker is
motivated to offer all categories that exist
( 
).
In real information filtering applications, one expects
to be quite small, since each consumer regards most information
as junk. It is useful to think of
as a (presumably tiny) spam regime,
in which it costs so little to send information,
and the financial impact on
a consumer of receiving junk is so minimal, that
it makes economic sense to send all articles to all consumers.
In between these two regimes, the optimal number of categories
is finite
.