In order to understand the behavior of more realistic economies in which brokers and consumers are less informed about the system state, and less immediately responsive to environmental changes, we have built an agent simulation environment that allows us to experiment with a wide range of utility maximization strategies for consumers and brokers. In particular, we do not assume that brokers know each other's prices (or interest vectors), nor that the brokers know the consumers' interest vectors. Instead, they must make do with historical data based on their own parameters (e.g. prices and interest vectors) and experience (e.g. consumer demand and profits).
Here we describe a simulation run involving
10,000 consumers, 500 brokers, and 100 categories.
In this run, a typical consumer was completely interested
( 
) in roughly 3 out of the 100 categories and completely
uninterested ( 
) in all other categories.
The computation and transport costs were 
and 
;
the information value was V = 150.
Under these circumstances, 
.
To set prices, the brokers use an extremely simple-minded
strategy: they randomly shift their price by
a small amount up or down. If (after a suitable period of time),
the broker finds that its profit per unit time has increased,
it keeps moving the price in the same direction; otherwise it
reverses direction. We call this a derivative-following
algorithm. Brokers adjust their interest vectors in a similar way,
increasing or decreasing 
by an amount depending
upon the profit or loss recently experienced when selling
an article in category j.
The brokers and consumers estimate the utility of adding
or cancelling subscriptions using a matchmaker that periodically
gauges agents' interests by issuing questionnaires about a given
set of articles.
Each consumer initially establishes a subscription with a single randomly chosen broker. From time to time, agents make asynchronous, independent decisions about adjusting prices, interest vectors, or subscriptions. Figure 4 shows the distribution of consumers' utilities at three different moments in their evolution. Starting from a state in which virtually all of the consumers have negative utilities, the economy adapts itself such that most consumers have positive utilities, and at worst a few have zero.
Of the original 500 brokers, only 122 remain active at time t=200,000 (i.e., after 200,000 articles have flowed through the system). The others have either gone broke or are not participating in the market because they are buying no articles from the news source. Many brokers die out within the first few thousand time steps, while others thrive at first but then suddenly start losing to competition. All of the 122 that remain at t=200,000 have chosen just a single category in which to specialize, and among them cover 86 distinct categories.
At t=0, almost all of the consumers have negative utility because the random initial conditions typically do not give them a large enough ratio of interesting articles to junk. Rapid improvements are soon made as the agents mutually sort out the subscription topology. During this phase, many consumers temporarily drop out of the economy, while the remaining ones eke some positive utility out of the brokers. Once a broker has a semi-coherent following, positive feedback sets in: the broker is encouraged by its clientele to provide articles that they will find interesting. Once the broker specializes to a small number of categories, other consumers are now attracted. By t=100,000, all of the brokers have specialized into a single category, and no consumers receive any junk.
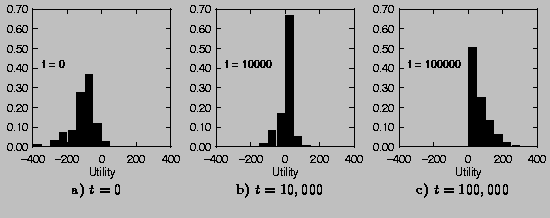
Figure 4: Evolution of the consumer utility distribution.
In this run, dramatic cyclical price wars were not observed, although more benign short-lived price wars played a role in driving superfluous brokers out of the market. Because the derivative-following price-setting algorithm forbids large discontinuous changes in prices, it appears unlikely to support dramatic cyclical price wars of the sort we found in the myoptimal case. Unfortunately, since the profit landscape typically contains several distinct humps separated by discontinuities, the derivative-following algorithm can often cause the economy to become stuck in highly suboptimal states. In other simulation runs in which the brokers initially offered an excessive number of categories, the system consistently evolved to a state in which no articles were sold. Making the system more robust to unfavorable initial conditions (or more responsive to environmental changes) requires permitting discontinuous jumps in price or interest vectors, but these capabilities also put the system at greater risk for cyclical price wars.