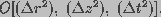 .
Here,
.
Here, 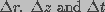 denote the computational intervals
in radius, length and time variables, respectively.
denote the computational intervals
in radius, length and time variables, respectively. Specific Aim: The proposed model will be used to determine the changes in membrane conductance and pore distribution under different applied field conditions. These studies will be performed by computer simulations of the electroporation model. The Crank-Nicholson finite difference method will be used to numerically solve the differential equations that describe the model. The simulation results will describe the dynamics of non-linear changes in membrane properties, such as membrane conductance and pore population, induced by an external electric field.
Experimental Methods and Materials:
The membrane-field interaction model described in section 3.1 will be used
to calculate distribution of membrane pores, transmembrane potential and
membrane conductance for different applied pulse amplitudes. These results
will be obtained by numerically solving the two partial differential equations
(Eq. 1 and Eq. 7) that represent the central ideas of the model. The coupled
partial differential equations describing the evolution of pores
and transmembrane potential distribution will be solved by a finite difference
method. In particular, the Crank-Nicholson implicit scheme (Anderson et al.
1984) will be used. This unconditionally stable method was chosen as it
provides a second-order accuracy with a
truncation error of 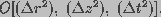 .
Here,
.
Here, 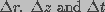 denote the computational intervals
in radius, length and time variables, respectively.
denote the computational intervals
in radius, length and time variables, respectively.
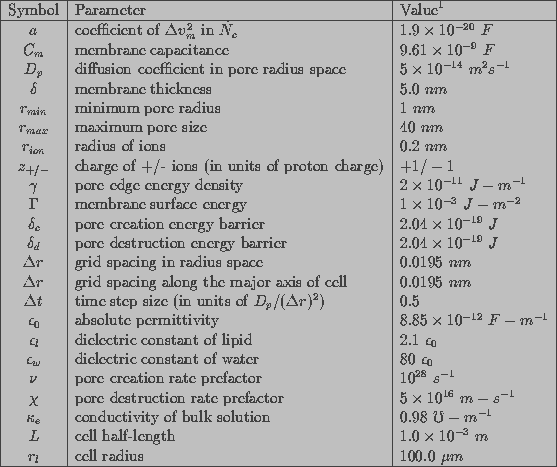
Table 1 shows values of simulation parameters used to characterize a cell
membrane and electric field in this model. A skeletal cell 1-mm in
length and 100- m in diameter will be studied. Cell membrane will be
divided into 1-
m in diameter will be studied. Cell membrane will be
divided into 1- m patches and these patches will be considered as
independent in their electrical properties. The preliminary
implementation and model verification were carried out on a Crimson VGX/T
computer (Silicon Graphics, Inc., Mountain View, CA). A series of
simulations for various pulse lengths and transmembrane potentials in the range
of 150 to 300 mV will be performed.
m patches and these patches will be considered as
independent in their electrical properties. The preliminary
implementation and model verification were carried out on a Crimson VGX/T
computer (Silicon Graphics, Inc., Mountain View, CA). A series of
simulations for various pulse lengths and transmembrane potentials in the range
of 150 to 300 mV will be performed.
Preliminary Results: The electroporation model was implemented on a computer using numerical techniques. An iterative scheme was developed to solve the partial differential equations representing the transmembrane potential distribution (Eq. 1) and pore distribution (Eq. 7). A series of simulations representing a voltage clamp experiment were performed. These simulations were used to determine transmembrane current and pore distribution as a function of transmembrane potential.
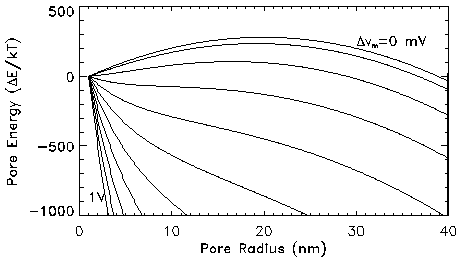
Pore Energy: The creation and expansion of membrane pores are controlled by the pore energy. Pore energy is a function of pore radius and transmembrane potential. It is the sum of a mechanical component and an electrical component. Figure 2 shows the total pore energy as a function of pore radius for different transmembrane potentials. The curve for zero transmembrane potential represents the mechanical contribution of the pore energy. This energy represents the sum of surface tension forces acting on the pore wall. It can be seen that a steep positive energy barrier exists for pore expansion at small pore radii. Thus, in the absence of a transmembrane potential or even at low transmembrane potentials, the pore energy favors reduction in pore size. At these transmembrane potentials, the energy gradient required to form a pore of large radius is inhibitive. Therefore, at low transmembrane voltages, most of the pores present on the membrane are of very small radius. Pores of small radii contract instantaneously due to the surface tension forces related to acting on the pore wall.
At higher transmembrane potentials, an expansive pressure contributes to an increase in pore size. This is evident from a decreasing energy profile for transmembrane potentials greater than 350 mV. The aqueous pores store more charge per area and experience a larger compressive pressure than lipid regions. This pressure difference results in expansion of the pore in the radial direction, so that as the transmembrane potential is increased, larger pore radii are favored. For r sufficiently large, the "drift flux" (second term in Smoluchowski equation) is much larger than the "diffusion flux" (the first term), and a pore with a large radius is unstable and can grow until the membrane ruptures. The value of pore radius at which this irreversible expansion occurs is referred to as the critical pore radius. It is seen from Fig. 2 that the value of critical radius decreases with an increase in transmembrane potential. The presence of these pores on the membrane gives rise to the electroporation current.
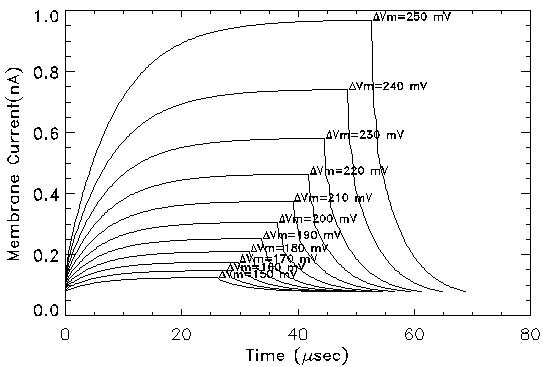
Electroporation Current: Initial simulations of the electroporation model were designed to simulate voltage clamp experiments (discussed in the next section). Figure 3 shows plots of transmembrane current as a function of time when the cell is clamped to different transmembrane potentials in the range from 150 to 250 mV. A resting transmembrane potential of 90 mV was assumed. The membrane was clamped to the indicated potential until the transmembrane current reached steady-state. The simulations indicate an exponential increase of transmembrane current at elevated potentials. The steady-state transmembrane current varies non-linearly with transmembrane potential. At potentials greater than 200 mV, a significant number of pores evolve to larger radii because of the decrease in pore energy as discussed in the previous paragraph. The relaxation of the electroporation current following removal of the voltage clamp pulse is independent of the transmembrane potential. This is in agreement with the experimental results. When the voltage clamp is removed, the pores experience a large negative parabolic energy barrier and thus shrink in size, leading to a decrease in transmembrane current. The time constant of relaxation is much smaller than that of evolution because of the difference in energy gradient experienced during and after the pulse.
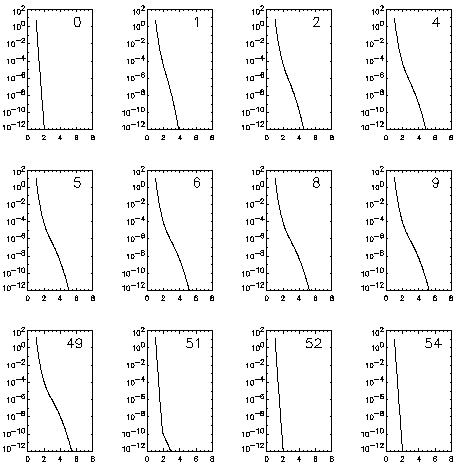
 s) following the application of the pulse is shown in
the top right corner of each plot. The pulse is turned off when the pore
distribution reaches steady-state, t=50
s) following the application of the pulse is shown in
the top right corner of each plot. The pulse is turned off when the pore
distribution reaches steady-state, t=50  s in this case.
s in this case.
Pore Distribution: The transmembrane current changes at
elevated transmembrane potentials discussed above are due to membrane
pore distribution. Figure 4 shows the distribution of
pores at different instants during and after a 250 mV pulse. Each plot
in the series relates to the number of pores within radius between r
and r+dr as a function of pore radius. The number at the top
right corner of each plot denotes the time (in  s) following the
application of the pulse. The bottom row of plots shows the relaxation
of pore distribution to initial conditions when the pulse is turned off
(at t = 50
s) following the
application of the pulse. The bottom row of plots shows the relaxation
of pore distribution to initial conditions when the pulse is turned off
(at t = 50 s). It is seen that the pores evolve to larger radii
in the presence of an imposed potential while new pores are formed at
minimum radius. This results in an increase in the total number of
pores thus increasing the transmembrane current. This increase in
membrane current correlates with the measurements of voltage clamp
experiments.
s). It is seen that the pores evolve to larger radii
in the presence of an imposed potential while new pores are formed at
minimum radius. This results in an increase in the total number of
pores thus increasing the transmembrane current. This increase in
membrane current correlates with the measurements of voltage clamp
experiments.