Potential flow codes represent an extremely efficient and accurate means to compute un-separated flow around complex geometries. The aim of this code project was to develop a code capable of rapidly solving potential problems around complex geometries in a rapid, hands-off manner.

FastAero2D

FastAero2D is a two-dimensional potential flow solver coupled with a simple spring-mass representation of the structural dynamics. The 2-Dimensional potential flow code exploits and iterative GMRES [6] solver for rapidly solving the linear system. The potential flow problem is discretized using linear basis functions on flat panels. Both a thin surface (velocity) formulation and a thick body (Greens Theorem Thick Body Formulation) have been developed. The unsteady 2-D wake vorticity is represented using a linear element freely convecting, self-influencing wake. As a result the wake will convect and roll-up under the local velocity influence (as seen in figure 1).

Figure 1: An example of the 2-Dimensional FastAero code applied to a simple heaving wing motion. In this example the fluid structure interaction is simplified using a leading edge spring to allow compliance. Although this model is a realistic model of natural flight, the example lends insight into the effect of leading edge torsion rod or bone compliance.

FastAero3D

FastAero3D[1] is an advanced, 3-Dimensional unsteady panel method solver developed at MIT. The code incorporates an accelerated iterative solution approach through the use of the precorrected-FFT[3] and Fast Multipole Algorithms[4] (Matrix Vector Product (MVP) acceleration).  Through the use of matrix-multiply accelerations, intermediate time-step solutions can be performed very rapidly. As such, the solution of highly resolved unsteady potential flows is possible.

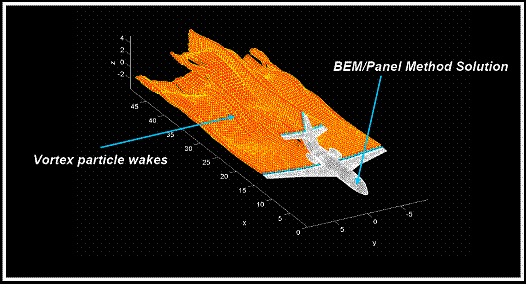
Figure: A plot of the FastAero3D solution around a business jet configuration. In this image the features of the FastAero3D solution are illustrated. The body of the business jet is represented using a boundary element surface triangular discretization. The localized vorticity in the wake is represented using the vortex particle method (VPM).

References

[1] Willis, D.J., Peraire, J. White, J.K., A combined pFFT-multipole tree code, unsteady panel method with vortex particle wakes, 43rd AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2005-0854, Reno, NV, Jan. 2005.

[2] Willis, D.J., Peraire, J. White, J.K., 'A quadratic basis function, quadratic geometry, high order panel method' presented at 44th AIAA Aerospace Sciences Meeting, AIAA-2006-1253, Reno , Nevada , 2006.

[3] Philips, J.R., White, J.K., A Precorrected-FFT Method for Capacitance Extraction of Complicated 3-D Structures, Proc. of the IEEE/ACM International Conference on Computer-Aided Design, pp. 268-271, November 1994.

[4] Greengard, L., Rokhlin, V. A Fast Algorithm for Particle Simulations,  J. Comput. Phys. 73, 325 (1987).

[5]  Rehbach, C. Calcul numerique d’ecoulement tridimensionels instationaires avec nappes tourbillonnaires, La Recherche Aerospatiale, pp. 289-298, 1977.

[6] Saad, Y. and Schultz, M. H. 1986. GMRES: a generalized minimal residual algorithm for solving nonsymmetric linea systems. SIAM J. Sci. Stat. Comput. 7, 3 (Jul. 1986), 856-869.

The current project has been funded by several different sources at different times. We are very thankful to the following funding sources:

Singapore-MIT Alliance (SMA), National Science Foundation (NSF), Natural Science and Engineering Councile of Canada (NSERC), and the Air Force Office of Scientific Research.