MaxwellFDFD
MaxwellFDFD is a MATLAB-based package that solves the frequency-domain Maxwell's equations
\[ \nabla \times \mathbf{E}(\mathbf{r}) = -i \, \omega \, \mu(\mathbf{r},\mathbf{\omega}) \, \mathbf{H}(\mathbf{r}) - \mathbf{M}(\mathbf{r}),\\ \nabla \times \mathbf{H}(\mathbf{r}) = i \, \omega \, \varepsilon(\mathbf{r},\mathbf{\omega}) \, \mathbf{E}(\mathbf{r}) + \mathbf{J}(\mathbf{r}), \]
where
\(\mathbf{r}\) is the position variable;
\(\mathbf{E}(\mathbf{r})\) and \(\mathbf{H}(\mathbf{r})\) are the solution electric and magnetic fields of the EM waves;
\(\mathbf{J}(\mathbf{r})\) and \(\mathbf{M}(\mathbf{r})\) are the electric and magnetic current source densities emanating the EM waves;
\(\omega\) is the oscillation frequency of the current sources; and
\(\varepsilon(\mathbf{r},\omega)\) and \(\mu(\mathbf{r},\omega)\) are the electric permittivity and magnetic permeability of the object at \(\mathbf{r}\) for \(\omega\).
MaxwellFDFD solves the above Maxwell's equations by the finite-difference frequency-domain (FDFD) method, and hence the name MaxwellFDFD.
Major Features
Built-in frequency-dependent dielectric constants for commonly used nanophotonic materials (e.g., Ag, Au, Si, SiO₂) taken from the widely used references (e.g., Johnson and Christy, Palik, CRC Handbook)
Dynamic nonuniform grid generation aligned with object boundaries
Waveguide mode solver and waveguide-mode-generating current source
2D and 3D visualization of objects, sources, and solution fields
Periodic array of objects
Electric (\(\mathbf{J}\)) and magnetic (\(\mathbf{M}\)) current sources
PEC, PMC, periodic, and Bloch boundary conditions
Stretched-coordinate perfectly matched layer (SC-PML) and uniaxial PML (UPML)
Total-field/scattered-field (TF/SF) method
Power flux calculation
System Requirements
MATLAB 2014a or later (no Toolbox needed)
Download
Press the “Download ZIP” button in the right panel of MaxwellFDFD's GitHub page.
Documentation
The online documentation is available here. (The entire MATLAB-style documentation is included in the doc/ directory of the downloaded MaxwellFDFD package.)
Examples
Plane wave incident on a slit in a silver slab
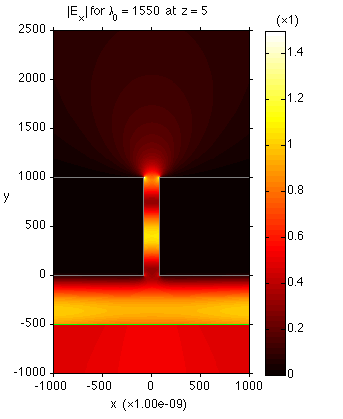 |
TF/SF simulation of a plane wave incident on a gold bow-tie antenna
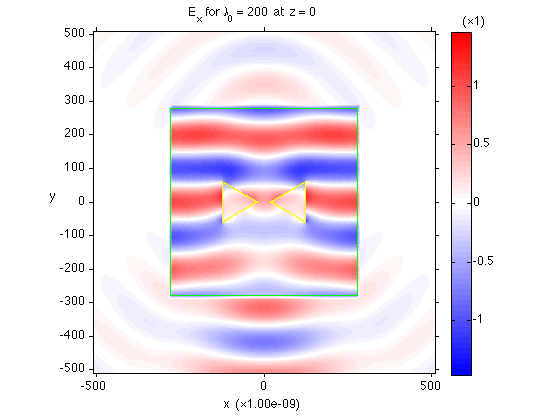 |
Point source in a photonic crystal waveguide double bend
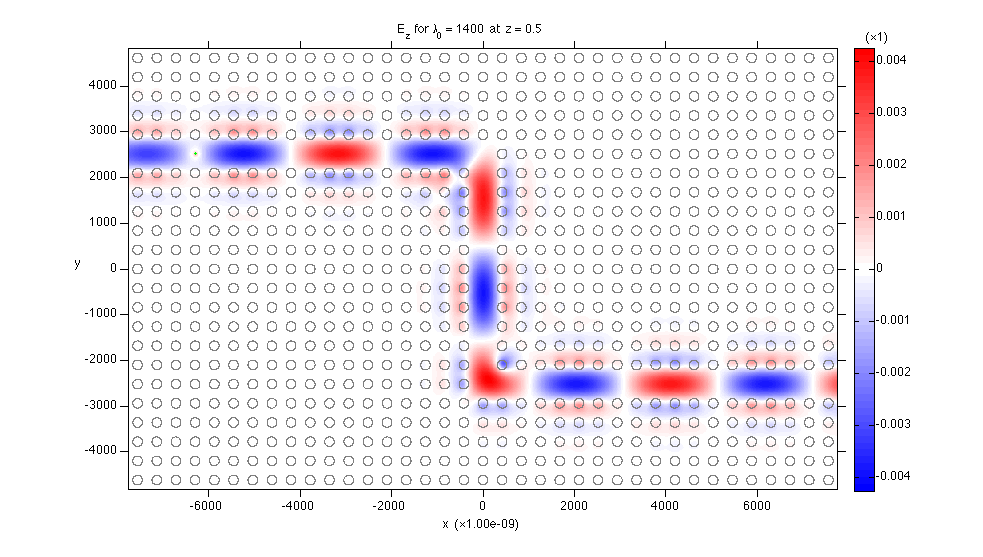 |
More examples: [link]
Basic Usage
Using MaxwellFDFD is very simple. There is an all-in-one function, maxwell_run(), and you just need to fill in its input parameters. For example, below is the code for the first example shown above.
[E, H] = maxwell_run(...
'OSC', 1e-9, 1550, ...
'DOM', {'vacuum', 'none', 1.0}, [-1100 1100; -1100 2600; 0 10], 10, BC.p, [100 100 0], ...
'OBJ', {'CRC/Ag', 'k'}, ...
Box([-1100 -80; 0 1000; 0 10]), ...
Box([80 1100; 0 1000; 0 10]), ...
'SRCJ', PlaneSrc(Axis.y, -500, Axis.x));
The meaning of the input parameter groups used in the code is as follows:
'OSC' (oscilation): the length unit (1 nm) and free-space wavelength (1550 nm)
'DOM' (domain): the material and size of the simulation domain
'OBJ' (object): the materials and shapes of the objects in the simulation domain
'SRCJ' (source): the electric current source in the simulation domain
The output parameters E and H are the solution E- and H-fields of the simulation.
How to Cite
You are welcome to cite the following paper about the techniques used in MaxwellFDFD:
W. Shin and S. Fan, “Choice of the perfectly matched layer boundary condition for frequency-domain Maxwell's equations solvers,” Journal of Computational Physics, vol. 231, pp. 3406–3431 (2012) [pdf]
You can also cite the URL of MaxwellFDFD's GitHub page as follows:
W. Shin, MaxwellFDFD Webpage, 2015. https://github.com/wsshin/maxwellfdfd
If you use LaTeX, here is the BibTeX record for the GitHub page:
@webpage{maxwellfdfd-webpage,
Author = {Wonseok Shin},
Note = {{https://github.com/wsshin/maxwellfdfd}},
Title = {{MaxwellFDFD} {W}ebpage},
Year = {2015}
}