INTRODUCTION
|
Shortly after shape grammars were invented by Stiny and
Gips, a two part project for shape grammars was outlined by Stiny. In a 1976 paper  ,Stiny described “two exercises
in formal composition”. These simple exercises became the foundation for the many
applications of shape grammars that followed, and suggested the potential of such
applications in education and practice. The first exercise showed how shape grammars could
be used in original composition, that is, the creation of new design languages or styles.
The second exercise showed how shape grammars could be used to analyze known or existing
design languages. Both exercises illustrated the unique characteristics of the shape
grammar formalism that helped motivate almost a quarter century of shape grammar work.
General but simple, formal yet intuitive: qualities that continue to make shape grammar
disciples and confound skeptics. ,Stiny described “two exercises
in formal composition”. These simple exercises became the foundation for the many
applications of shape grammars that followed, and suggested the potential of such
applications in education and practice. The first exercise showed how shape grammars could
be used in original composition, that is, the creation of new design languages or styles.
The second exercise showed how shape grammars could be used to analyze known or existing
design languages. Both exercises illustrated the unique characteristics of the shape
grammar formalism that helped motivate almost a quarter century of shape grammar work.
General but simple, formal yet intuitive: qualities that continue to make shape grammar
disciples and confound skeptics.
|
Shape grammar theory and applications are well documented
and represented in the literature on design computation and related areas. A shape grammar
is a set of shape rules that apply in a step-by-step way to generate a set, or language,
of designs. Shape grammars are both descriptive and generative. The rules of a shape
grammar generate or compute designs, and the rules themselves are descriptions of the
forms of the generated designs.
|
Shape grammars have properties aimed at making them
especially suitable for designing, without sacrificing formal rigor. First, the components
of shape rules are shapes: points, lines, planes, or volumes. Shape rules generate designs
using the shape operations of addition and subtraction, and spatial transformations
familiar to designers such as shifting, mirroring, and rotating. In short, shape grammars
are spatial, rather than textual or symbolic, algorithms. Second, shape grammars treat
shapes as nonatomic entities--they can be freely decomposed and recomposed at the
discretion of the designer. This liberty allows for emergence--a feature that
distinguishes shape grammars from set grammars, the most common kind of formal grammar.
Emergence is the ability to recognize and, more importantly, to operate on shapes that are
not predefined in a grammar but emerge, or are formed, from any parts of shapes generated
through rule applications. Third, shape grammars are nondeterministic. The user of a shape
grammar may have many choices of rules, and ways to apply them, in each step of a
computation. As a design is computed, there may be multiple futures for it that respond
differently to emergent properties, or to other conditions or goals.
|
To the right is a two-rule grammar that illustrates these
properties. The first rule shifts a square halfway along a diagonal axis of the square.
The second rule shifts an L-shape, also along a diagonal axis. Registration marks in each
rule show the positions of the shapes on the left-side and right-side of the rule relative
to each other. The starting shape for computations, called the initial shape, consists of
two L-shapes. The two rules apply to this shape and to shapes produced from it by matching
the square or L-shape on the left-side of either rule with a square or L-shape in a
design. The square or L-shape in either rule may be translated, rotated, reflected, or
scaled in order to match a shape in a design. If a match is made, the matched shape in the
design is then replaced with a shifted shape as indicated in a rule. The direction of the
shift depends on the spatial transformation used to make the match.
|

initial shape
 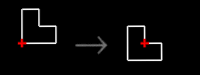
rules
|
Below is a computation of a design using the grammar. From
the second step on, the rules can apply to either emergent L-shapes or emergent squares.
Also from the second step on, either the first or the second rule can be applied to a
design. The user of the grammar, human or machine, must decide which rule to apply and to
which shape in a design to apply the rule.
|
 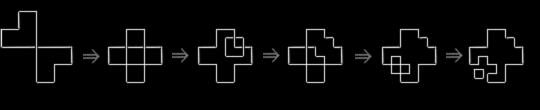 a a
|
Below is another computation using the grammar. The
computation is identical to the one above in the first three steps. Then it diverges and
follows a different path to produce a different design. Many other computations are
possible with the grammar.
|
 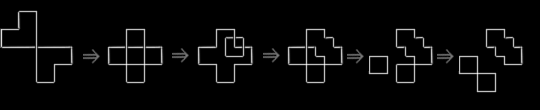 a a
|
Shape grammar theory has advanced over the years to
include complexities of shapes and shape computations beyond what is illustrated above.
Parametric shape grammars  compute designs with variable or parametric shapes. Color grammars compute designs with variable or parametric shapes. Color grammars  and grammars with weights and grammars with weights  compute designs with shapes
and properties of shapes (such as color, material and function). Description grammars compute designs with shapes
and properties of shapes (such as color, material and function). Description grammars  compute descriptions of
designs. Structure grammars compute descriptions of
designs. Structure grammars  compute designs as structures or sets of shapes. Attributed grammars compute designs as structures or sets of shapes. Attributed grammars  compute designs with
attributes and constraints on attributes. Parallel grammars or grammars defined in
multiple algebras compute designs with
attributes and constraints on attributes. Parallel grammars or grammars defined in
multiple algebras  simultaneously compute different shape, text, or symbolic
representations of designs (for example, plans, sections, and elevations together with
verbal descriptions of them). All of these extensions to the original shape grammar
formalism have been developed in order to compute certain kinds of designs more easily or
expressively than with a standard shape grammar. However, none add to the computational
power of a standard shape grammar which is equivalent to a Turing Machine, the most
powerful computational device yet defined. simultaneously compute different shape, text, or symbolic
representations of designs (for example, plans, sections, and elevations together with
verbal descriptions of them). All of these extensions to the original shape grammar
formalism have been developed in order to compute certain kinds of designs more easily or
expressively than with a standard shape grammar. However, none add to the computational
power of a standard shape grammar which is equivalent to a Turing Machine, the most
powerful computational device yet defined.
|
The history of shape grammar applications in
architecture and the arts for the two complementary problems of original design and
analysis is sketched in the first section of this paper. These two categories of
applications do not have rigid boundaries, and are used mainly as a framework for
discussion. An overview of the roles of shape grammar applications in education
and practice is given in the second section. New and ongoing issues concerning
shape grammars in education and practice are discussed in the last section.
|




