Abstract
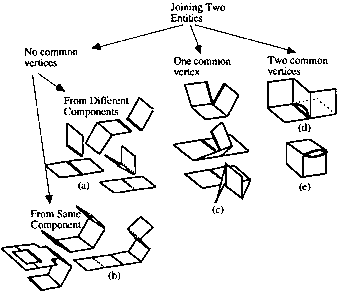
This paper proposes the use of a thin-walled primitive for modeling the geometry of inherently thin objects. The authors suggest a topological invariant supporting both manifold and thin-walled non-manifold objects based on this primitive. The paper establishes a general topological invariant s + e - v - gnm + m - f = 0 regarding the number of components, edges, vertices, holes, volumes, and faces, respectively. Corresponding Euler operators are derived, providing a basis for a modeling system for thin-walled objects. The validity of the proposed invariant constitutes a necessary condition for the validity of a geometrical representation of thin-walled products from a topological point of view. The paper also discusses merging the proposed general formula with standard manifold topology. It specifically proposes the use of non-integer values in the standard Euler-Poincaré formula for representing non-manifold components, thus permitting the use of thin-walled primitives with topological coherence to traditional solid geometry schemes.
