


Next: TOPEX/POSEIDON Altimetry
Up: Model and Data Configuration
Previous: Model and Data Configuration
The MIT Ocean General Circulation Model employs the incompressible
Navier-Stokes equations under the Boussinesq approximation and hydrostatic
balance (Jamous, Hill, Adcroft, and Marshall,1997). The model domain is the
northwest corner of the North Atlantic Ocean including the Labrador Sea proper
as well as some of the outlying Atlantic Ocean. The domain goes as far east as
the Mid-Atlantic Ridge and as far south as Newfoundland. The highly energetic
North Atlantic Current flows through the southeast corner of the domain. The
bottom topography is based on ETOPO5 data. The north and west boundaries are
closed; hence, there is no Davis Strait inflow and a very small portion of the
Denmark Strait is closed. The Davis Strait actually contributes 2 Sverdrups of
very cold, fresh input to the Labrador Sea, and can not be considered a
negligible effect (R. Pickart, personal communication). The south and east
boundaries are open. The model resolution is [1/8] of a degree latitude by
[1/5] of a degree longitude with 34 vertical levels. Therefore, the size of one
snapshot of the field is 176 by 185 by 34. The gridpoint separation is between
8.4 km and 15.7 km zonally and 13.9 km meridionally. The Rossby radius of
deformation is very small at high latitudes, which makes this nominally an
eddy-resolving model.
The model is run for one year with a time step of
15 minutes with the intent to realistically simulate October 1996-September
1997. The model's temperature and salinity (T-S) structure is initialized with
a Labrador Sea high resolution climatology produced by M. Visbeck, but with
zero velocity. There is no spinup time for the model to reach an equilibrium
state, therefore model drift must be investigated. The open boundaries have a
5-gridpoint sponge layer in which temperature and salinity are relaxed to the
Visbeck climatology. The relaxation coefficient decreases linearly in the
sponge layer to smoothly transition to the interior. The strongest relaxation
to the Visbeck data set is in the outermost gridpoint with a relaxation
timescale of 1 day. The Visbeck data set only includes a summer and a winter
state so the time-varying boundary conditions are derived from a
sinusoidally-varying interpolation of the full seasonal cycle. However, the
sponge layer is also relaxed to velocity profiles from a global model run
(courtesy D. Stammer). One source of inconsistency in the model may be the
fact that the boundary conditions are acquired from two different sources. The
boundaries will consequently not be in thermal wind balance. One suggestion to
resolve this problem is to compute relative velocity from the M. Visbeck
density profile and to acquire the vertical mean velocity from the D. Stammer
global model. Output from 2 model runs (as adapted and implemented for the
Labrador Sea by J. Sheinbaum) will be presented here: run 1 (10 day average
output) forced by a 2 degree resolution global state estimation, and run 2 (1
day averaged output) forced by a 1 degree resolution global model run. The
model runs of Stammer give output once a month. Therefore, the velocity
boundary conditions are interpolated linearly in space and time to the higher
resolution of this Labrador Sea model. Both the velocity and T,S boundary
conditions extend to the full depth of the water column. Surface boundary
conditions must also be supplied to the model. Twice-daily surface windstresses
are used from the NCEP Reanalysis. Daily NCEP sensible and latent heat fluxes
and precipitation values are used. Surface pressure is computed according to a
free surface formulation and is equivalent to the weight of the sea surface
height anomaly. Surface temperature and salinity are restored to the M. Visbeck
data with a 30 day relaxation timescale.
Biharmonic parameterizations of
momentum , temperature, and salinity are used in the model. Lateral diffusion
is assumed to be proportional to 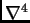 with a coefficient of
with a coefficient of
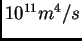 . Vertical diffusion depends on the second vertical derivative of
momentum, heat and salt with a coefficient of
. Vertical diffusion depends on the second vertical derivative of
momentum, heat and salt with a coefficient of
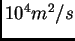 . These
diffusivities are independent of depth. Bottom friction is dependent on total
absolute velocity with a coefficient of
. These
diffusivities are independent of depth. Bottom friction is dependent on total
absolute velocity with a coefficient of
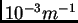 . Convective plumes
are not explicitly resolved in the model and must be adequately parameterized
in order to accurately predict water mass properties. The convective scheme
checks for unstable profiles every 30 minutes (run 1) or every 12 hours (run 2)
and mixes pairs of unstable levels once. A delicate balance exists between the
frequency of convection and lateral diffusion (J. Sheinbaum, personal
communication).
. Convective plumes
are not explicitly resolved in the model and must be adequately parameterized
in order to accurately predict water mass properties. The convective scheme
checks for unstable profiles every 30 minutes (run 1) or every 12 hours (run 2)
and mixes pairs of unstable levels once. A delicate balance exists between the
frequency of convection and lateral diffusion (J. Sheinbaum, personal
communication).
A comparison of the two model runs shows that run 1
handles the late winter convection much better. Run 2 , which used convective
adjustment only every 12 hours, produced very noisy vertical velocity
fields. Point-by-point comparisons of absolute sea surface height tend to
diverge after the convective season. Therefore, run 1 will be used
predominantly in comparisons with data. Run 2 will be used only in the spectral
description of the model since the output is in 1-day averages and gives a
wider frequency range. Special care will be used in judging the high frequency
content of run 2.



Next: TOPEX/POSEIDON Altimetry
Up: Model and Data Configuration
Previous: Model and Data Configuration
Jake Gebbie
2003-04-10