------
(s+10)
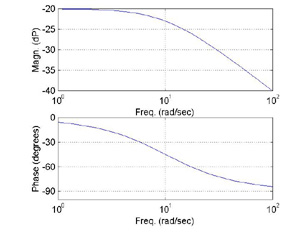
------
(s+10)^2
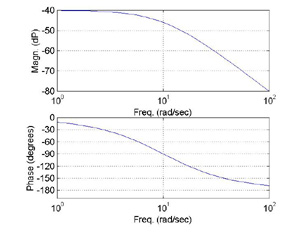
------
(s+10)^3

--------
(s+10)^3

| Top | Prev | Next |
| Delta in Gain slope (dB/dec)...
...with each Pole (or Zero) |
Delta in Phase (degrees)...
...with each Pole (or Zero) | |
| for EACH POLE | -20 (db/dec) | -90 (degrees) |
| for EACH ZERO | +20 (db/dec) | +90 (degrees) |
| 1 Pole | 2 Poles | ||||
| 1 ------ (s+10) |
= |  |
1 ------ (s+10)^2 |
= |  |
| 3 Poles | 3 Poles? but 1 Zero cancels 1 Pole! | ||||
| 1 ------ (s+10)^3 |
= |  |
(s+10) -------- (s+10)^3 |
= |  |
| gonzo@mit.edu | 2.010 Tutorial #2, 21-Sep-00 |