On 22 January, David Burt wrote a curious looking recurrence relation on our office whiteboard that read as follows \[x_{i + 1} = x_{i} + \frac{1}{x_{i}}~. \qquad (1)\]

The goal was to derive some growth bounds on \(x_{i}\), specifically that \(x_{i} \in \Omega(f(i)), x_{i} \in O(g(i))\) for some functions \(f, g\). After spending some time with some incorrect guesses, this was a growth bound I could show:

Proposition A: Let \(\{x_{i}\}_{i \geq 0}\) be generated by Eq. \((1)\) above with \(x_{0} > 0\). Then,

  1. for all \(i \geq 0\), \(x_{i} \geq \sqrt{x_{0}^{2} + 2i}\), and
  2. for all \(i \geq 0\), \(x_{i} \leq \sqrt{x_{0}^{2} + 2i + \frac{i}{x_{0}^{2}}}\).

Proof: By definition, for any \(j \geq 0\), \[x_{j + 1} - x_{j} = \frac{1}{x_{j}} ~; \quad x_{j + 1} + x_{j} = 2x_{j} + \frac{1}{x_{j}}~.\] Hence, multiplying these equations gives \[x_{j + 1}^{2} - x_{j}^{2} = 2 + \frac{1}{x_{j}^{2}}~.\] Summing both sides from \(j = 0\) to \(j = i - 1\) yields \[x_{i}^{2} - x_{0}^{2} = 2i + \sum_{j=0}^{i - 1}\frac{1}{x_{j}^{2}}~.\] Note that the sequence \(\{x_{i}\}_{i \geq 0}\) is increasing, and therefore \(x_{j} \geq x_{0} > 0\) for all \(j \geq 0\). Consequently, we have two bounds \[2i \leq x_{i}^{2} - x_{0}^{2} \leq 2i + \frac{i}{x_{0}^{2}}~,\] which completes the proof.

Clearly, these bounds can be improved. Note that we are ignoring the growth of the sequence in two places: 1) in the lower bound when using the fact that \(\frac{1}{x_{j}^{2}} > 0\), and 2) in the upper bound when using the fact that \(x_{j} \geq x_{0}\). Accounting for the progression of the sequence yields the following improved upper and lower bounds.

Proposition B: Let \(\{x_{i}\}_{i \geq 0}\) be generated by Eq. \((1)\) above with \(x_{0} > 0\). Then, for all \(i \geq 1\), \[x_{i} \leq \frac{1}{2x_{0}} + \sqrt{\frac{1}{4x_{0}^{2}} + 2k - 1 + x_{0}^{2}}~.\]

Proof: We begin by using the following inequality, which can be viewed as an application of Hölder's inequality. \[\sum_{j = 0}^{i - 1} \frac{1}{x_{j}^{2}} = \sum_{j = 0}^{i - 1} \frac{1}{x_{j}}\frac{1}{x_{j}} \leq \left(\max_{j \in \{0, \ldots, i - 1\}} \frac{1}{x_{j}}\right) \left(\sum_{j = 0}^{i - 1} \frac{1}{x_{j}}\right)~.\] Since the sequence \(\{x_{i}\}_{i \geq 0}\) is increasing, the maximum is \(\frac{1}{x_{0}}\). Due to the recurrence, \[\sum_{j = 0}^{i - 1} \frac{1}{x_{j}} = \sum_{j = 0}^{i - 1} (x_{j + 1} - x_{j}) = x_{i} - x_{0}~.\] Continuing from the previous proof, this yields the upper bound \[x_{i}^{2} - x_{0}^{2} \leq 2i + \frac{x_{i}}{x_{0}} - 1 \quad \Leftrightarrow \quad x_{i}^{2} - \frac{x_{i}}{x_{0}} - (2i - 1 + x_{0}^{2}) \leq 0~.\] When \(i \geq 1\), \(2i - 1 + x_{0}^{2} \geq 0\) and by Vieta's formula, this implies that there is a positive root (as the discriminant is \(> 0\)). Consequently, we get an upper bound as given by the positive root of the quadratic on the left hand side as \[x_{i} \leq \frac{1}{2x_{0}} + \frac{1}{2}\sqrt{\frac{1}{x_{0}^{2}} + 4(2i - 1 + x_{0}^{2})}~,\] which completes the proof.

Proposition C: Let \(\{x_{i}\}_{i \geq 0}\) be generated by Eq. \((1)\) above with \(x_{0} > 0\). Then, for all \(i \geq 2\), \[x_{i} \geq -\frac{x_{0}}{i - 1} + \sqrt{\left(\frac{i}{i - 1}\right)^{2}\left(\frac{x_{0}^{2}}{i} + \frac{i - 1}{i}\left\{2i + x_{0}^{2} + \frac{x_{0}^{2}}{i}\right\}\right)}~.\]

Proof: From the Cauchy-Schwarz inequality, we have \[\left(\sum_{j = 0}^{i - 1} \frac{1}{x_{j}}\right)^{2} = \left(\sum_{j = 0}^{i - 1} \frac{1}{x_{j}} \cdot 1\right)^{2} \leq i \cdot \sum_{j = 0}^{i - 1} \frac{1}{x_{j}^{2}} ~.\] Owing to the recurrence the left hand side from above is exactly \[\left(\sum_{j = 0}^{i - 1} \frac{1}{x_{j}}\right)^{2} = \left(\sum_{j = 0}^{i - 1}(x_{j + 1} - x_{j})\right)^{2} = (x_{i} - x_{0})^{2}~.\] Continuing from the proof of Proposition A, we get \[x_{i}^{2} - x_{0}^{2} \geq 2i + \frac{1}{i}(x_{i} - x_{0})^{2} \quad \Leftrightarrow \quad x_{i}^{2}\left(1 - \frac{1}{i}\right) + \frac{2x_{i}x_{0}}{i} - \left(2i + x_{0}^{2} + \frac{x_{0}^{2}}{i}\right) \geq 0.\] By Vieta's formula, the quadratic on the left hand side of the equivalent inequality has a positive root (as the discriminant is \(> 0\)). Consequently, we get a lower bound as given by the positive root of this quadratic as \[x_{i} \geq \frac{i}{2 (i - 1)} \left(-\frac{2x_{0}}{i} + \sqrt{\frac{4x_{0}^{2}}{i^{2}} + \frac{4(i - 1)}{i}\left\{2i + x_{0}^{2} + \frac{x_{0}^{2}}{i}\right\}}\right)~,\] which completes the proof.

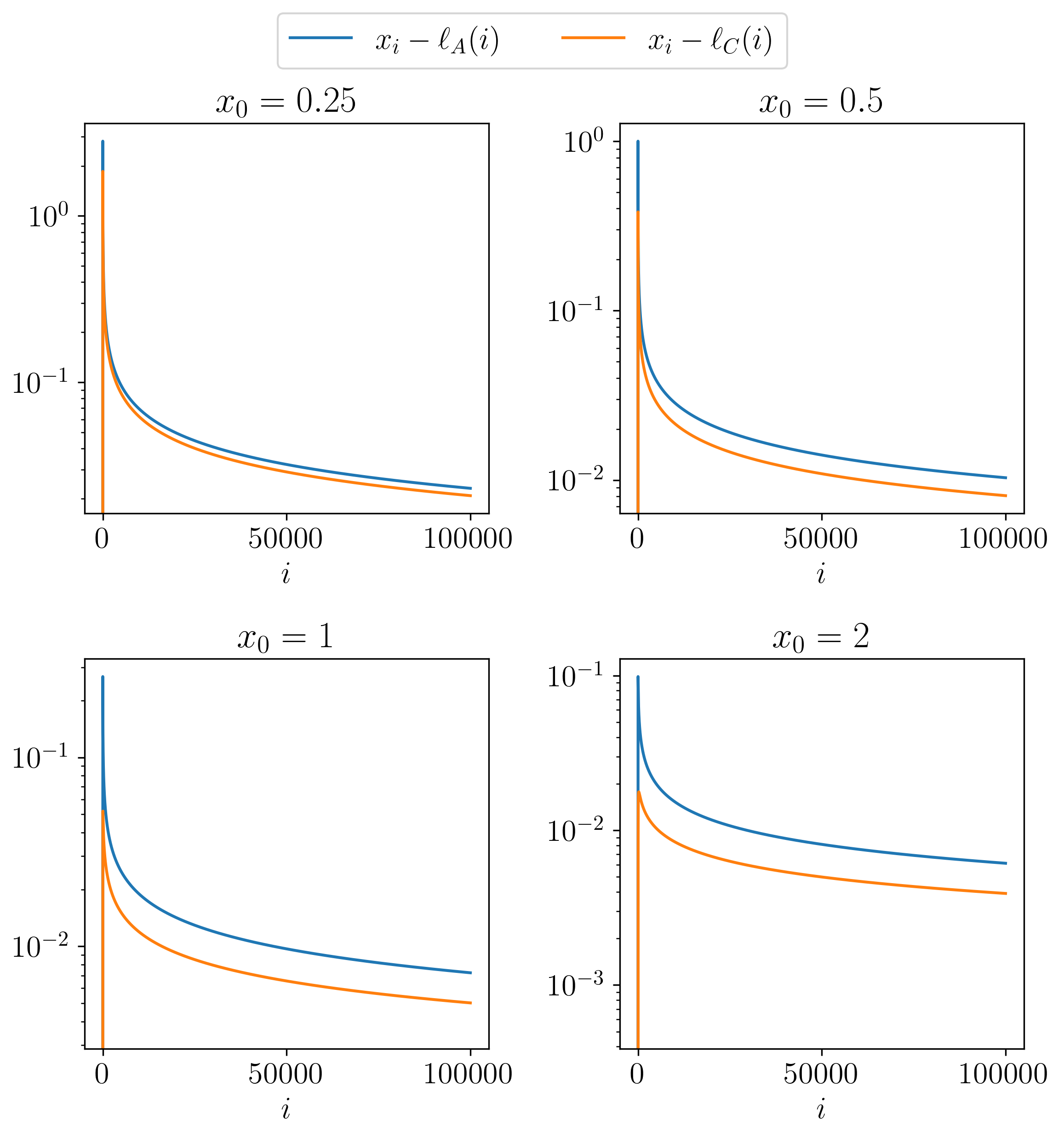
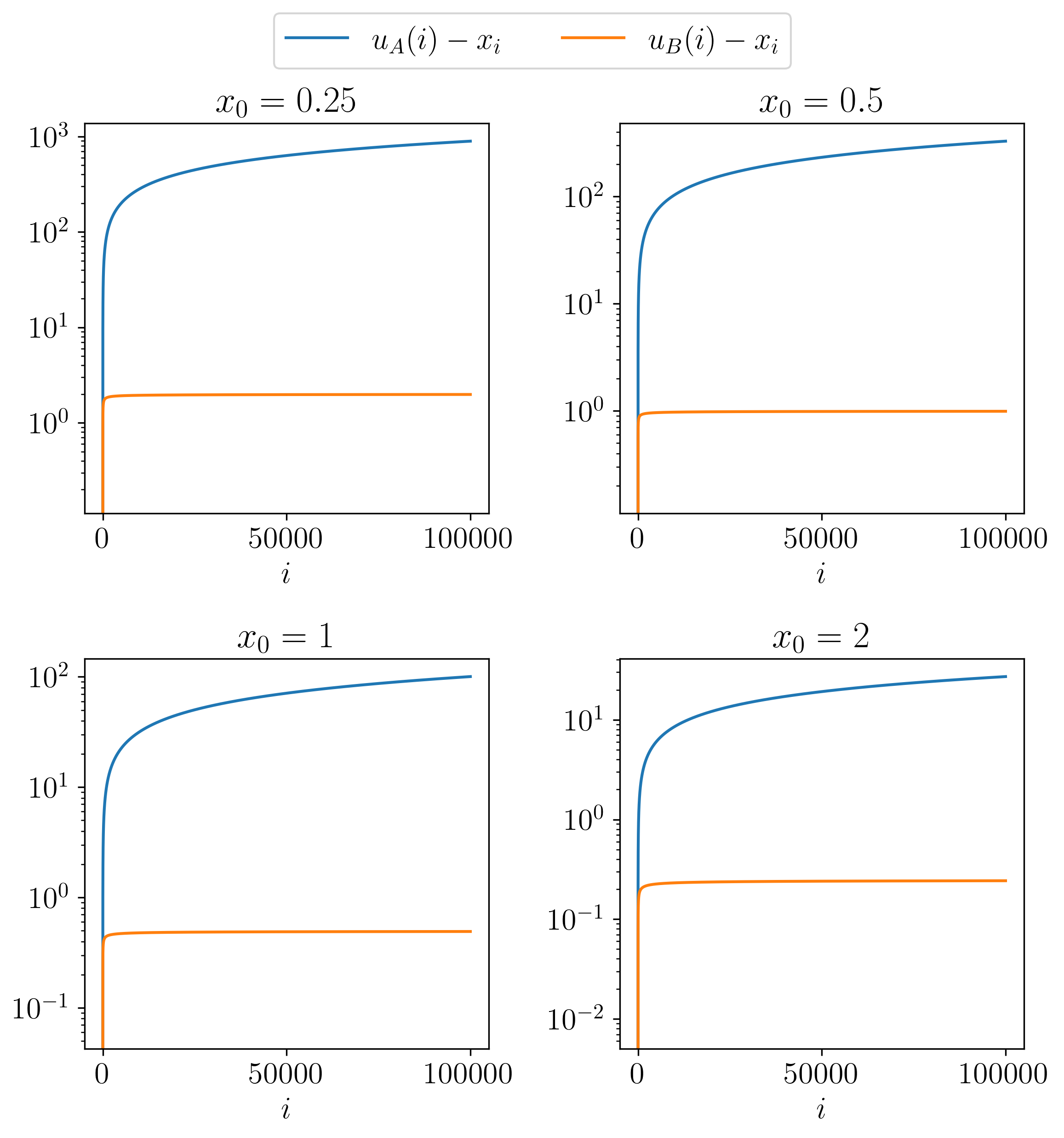
Propositions B and C appear to provide much better bounds on the growth of the sequence of interest. Below, we initialise the sequence at a collection of 4 values and plot the error to the actual values i.e., \(x_{i} - \ell(i)\), and \(u(i) - x_{i}\), where \(\ell, u\) are lower and upper bound functions respectively.

error plot for lower bound

Errors for lower bounds

error plot for upper bound

Errors for upper bounds

\(\ell_{A}\) and \(u_{A}\) are the lower and upper bound functions derived in Proposition A, \(u_{B}\) is the upper bound function derived in Proposition B, and \(\ell_{C}\) is the lower bound function derived in Proposition C. Both lower bounds have decreasing errors, and the refined lower bound function \(\ell_{C}\) has a better error compared to the naive lower bound function \(\ell_{A}\). Interestingly, the upper bounds appear to have an increasing error, but the error of the refined upper bound function \(u_{B}\) appears to have plateaued at a constant error.

Consider a more general recurrence relation \[x_{i + 1} = x_{i} + \frac{1}{x_{i}^{p}}~ \qquad (2)\] where \(p \in \mathbb{N}\) instead of \(p = 1\). In the same manner as Proposition A, it is possible to derive growth bounds for this recurrence.

Proposition D: Let \(\{x_{i}\}_{i \geq 0}\) be generated by Eq. \((2)\) above with \(x_{0} > 0\). Then,

  1. for all \(i \geq 0\), \(x_{i} \geq \left(x_{0}^{p + 1} + (p + 1)i\right)^{\frac{1}{p + 1}}\)
  2. for all \(i \geq 0\), \(x_{i} \leq \left(x_{0}^{p + 1} + (p + 1)i\left\{1 + \frac{1}{x_{0}^{p + 1}}\right\}^{p}\right)^{\frac{1}{p + 1}}\)

Proof: By definition, for any \(j \geq 0\), \[x_{j + 1}^{p + 1} - x_{j}^{p + 1} = (x_{j + 1} - x_{j}) \left(\sum_{m = 0}^{p} x_{j + 1}^{m} x_{j}^{p - m}\right) = \frac{1}{x_{j}^{p}} \left(\sum_{m = 0}^{p} \left\{\frac{x_{j + 1}}{x_{j}}\right\}^{m} x_{j}^{p}\right) = \sum_{m = 0}^{p} \left\{1 + \frac{1}{x_{j}^{p + 1}}\right\}^{m}~.\] Summing both sides from \(j = 0\) to \(j = i - 1\) yields \[x_{i}^{p + 1} - x_{0}^{p + 1} = \sum_{j = 0}^{i - 1}\sum_{m = 0}^{p} \left\{1 + \frac{1}{x_{j}^{p + 1}}\right\}^{m}~.\] Note that the sequence \(\{x_{i}\}_{i \geq 0}\) is increasing, and therefore \(1 \leq 1 + \frac{1}{x_{j}^{p + 1}} \leq 1 + \frac{1}{x_{0}^{p + 1}}\) for all \(j \geq 0\). Consequently, we have two bounds \[(p + 1)i \leq x_{i}^{p + 1} - x_{0}^{p + 1} \leq (p + 1)i \cdot \left(1 + \frac{1}{x_{0}^{p + 1}}\right)^{p}~.\] This completes the proof.

Some followup questions: