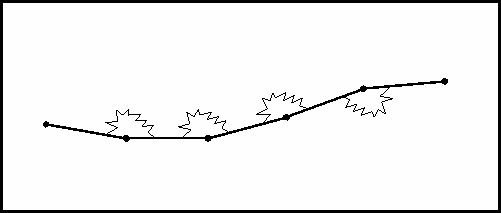
Another aspect of DNA packing utilizing the Kuhn segment concept is to consider the amount of energy required to bend each segment so that the chain as a whole can be wound into a coil inside the capsid. If we consider each Kuhn segment connected to its nearest neighbors by a torsion spring of spring constant K, then we can calculate the amount of energy required to bend it into a coil of radius R.

[DNA as a chain of Kuhn segments connected by torsion springs.]

Fortunately there is a relation that we can take advantage of to figure out the stiffness of the torsion spring between each segment. This relation is K = L_p k_BT. From this we can see that the persistence length is a characteristic length scale that relates the bending rigidity of the DNA chain to the thermal energy. Larger persistence lengths indicate a stiffer chain that is less susceptible to thermal fluctuations.

What we're interested in, of course, is the energy cost for bending the DNA into the nice round coil it must be in to fit in the capsid. Like a linear spring where the energy is of the form E = 1/2 k x², the energy to bend the DNA chain is of the form E = 1/2 K L (dt/ds)², where dt/ds is the derivative of the tangent vector to each Kuhn segment of the chain. Since the chain is being bent into a circle of radius R, dt/ds = 1/R, and thus the bending energy is E = 1/2 K L/R² = 1/2 L_p L/R² k_BT. If we assume that all of the DNA is coiled around the outer radius of the capsid (R = 42 nm), then the energy cost due to bending is E_bend = 1/2 * (50 nm)*(6800 nm)/(42 nm)² k_BT ~ 10² k_BT. Note that this is approximately the same energy cost as we found for the loss of entropy. From the model shown on the first page of the website, you may have noticed that some of the DNA is in fact coiled at smaller radii than the outermost "shell". The energy cost for bending that part of the DNA will be much higher since E is proportional to 1/R², but even so, it is unlikely that this energy cost greatly exceeds ~10³ k_BT.