Mean Field Approach

A discrete fitness landscape over a large number of equivalent sites (the complete graph), enables a self-consistent (mean-field) approach.

            

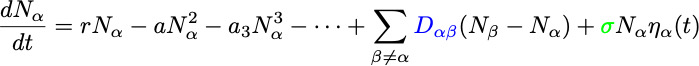
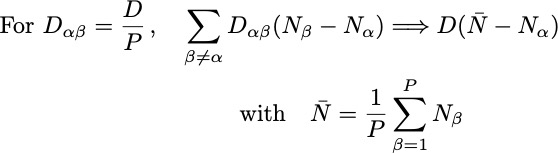
 While    are random variables (distributions), in the large  limit    is a number, leading to

The probability distribution function for   then evolve according to the Fokker-Planck equation

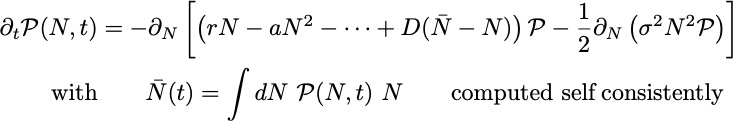
[Van den Broeck+Parrondo+Amero+Hernandez-Machado (1994); ....]

[J.-P. Bouchaud &  M. Mezard, Physica A 282, 535 (2000)]  [Munoz, Colaiori, Castellano, PRE 72, 056102 (2005)]

 Setting the time dependence to zero, leads to the (unnormalized) steady state distribution [PRE 102, 052106 (2020)]

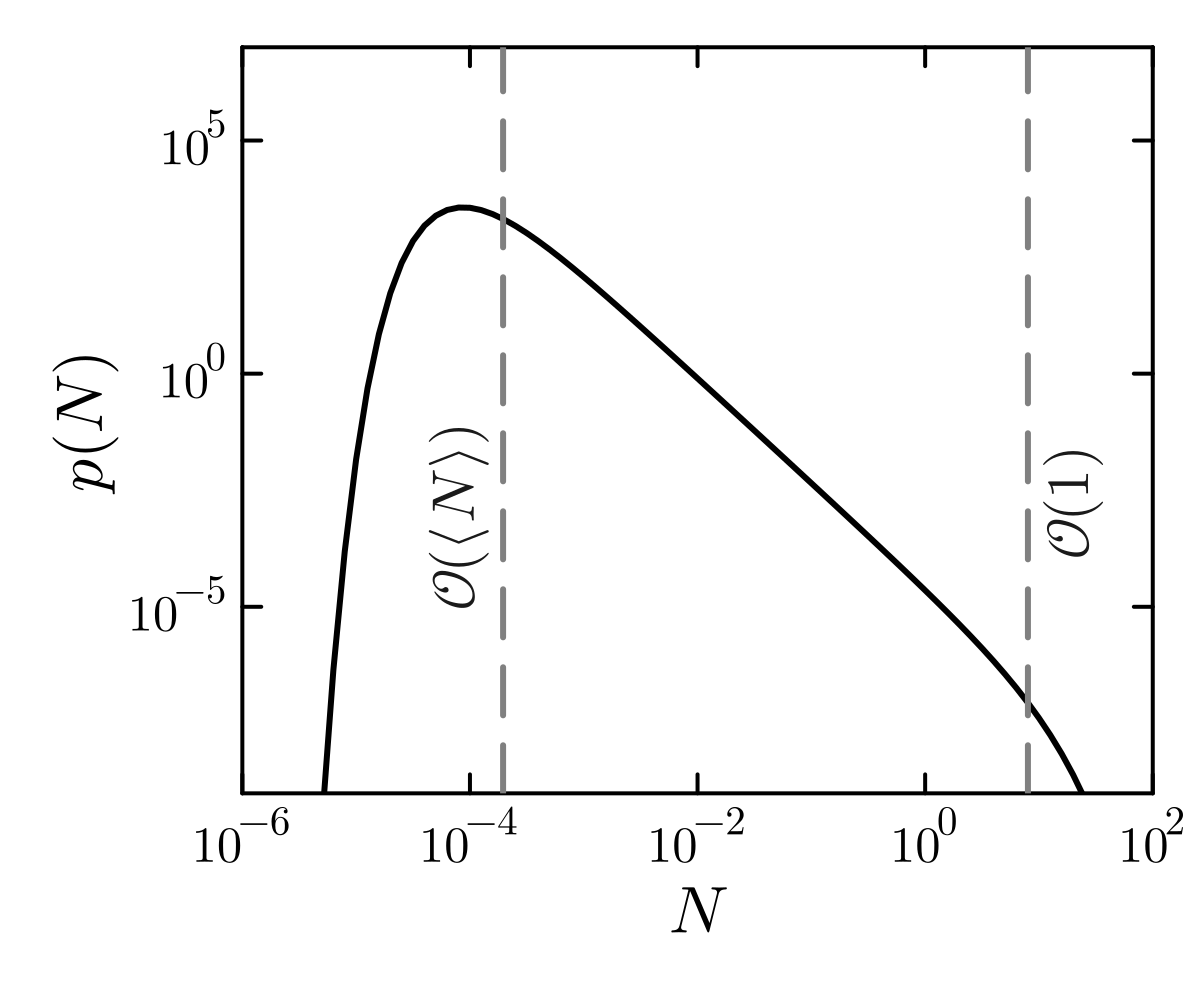
Power law distribution (consequence of multiplicative noise) with

small size cutoff set by dispersal and mean number, and

large size cutoff set by saturating terms.

Next (Extinction) Outline Growth & saturation Mean field analysis Extinction on a seascape Growth on a seascape Diversity vs Stability Coexistence on a seascape Phase behavior Summary