Growth & Saturation

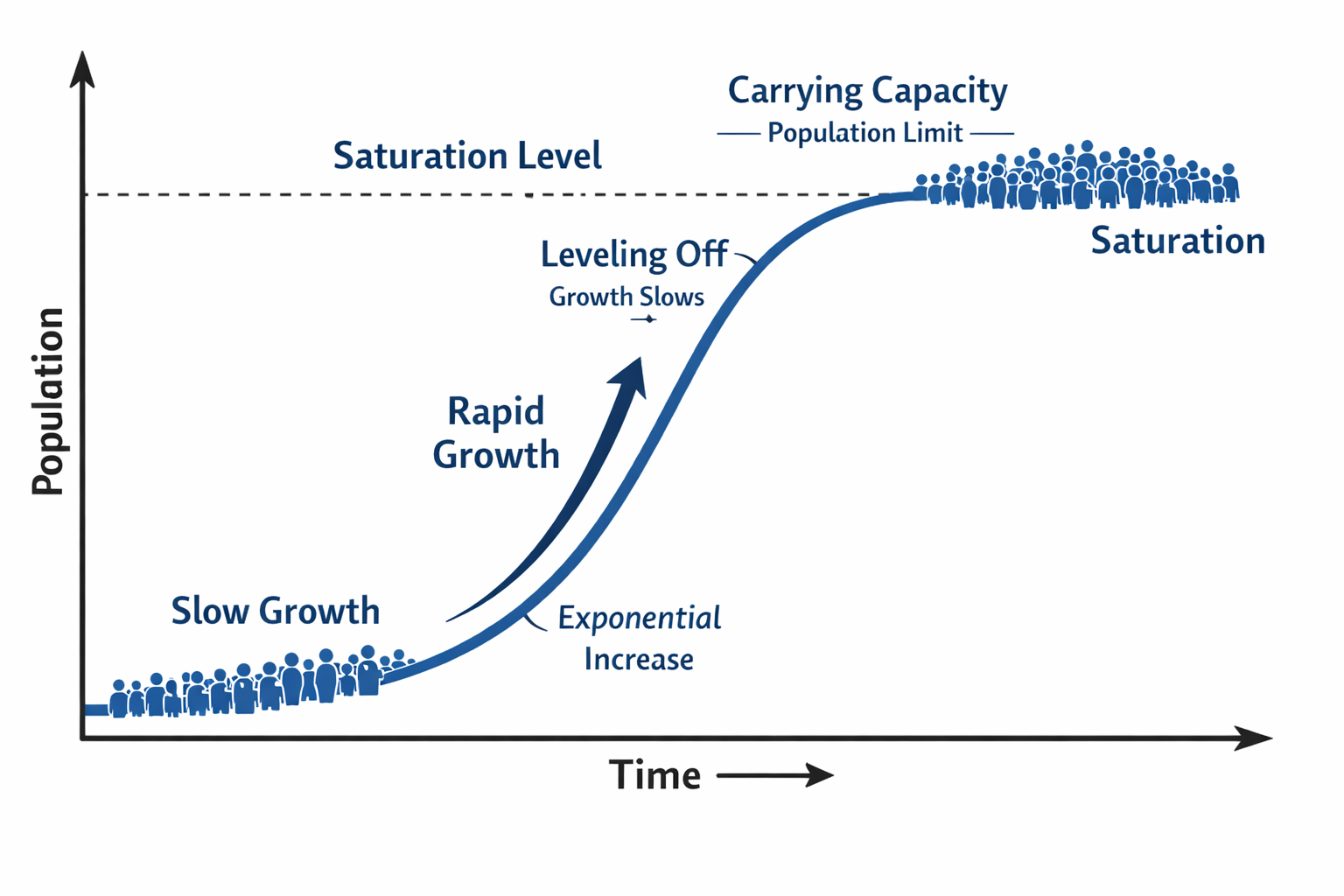
 Sigmoid curves abound in describing population growth

From https://www.slideshare.net/JackieAndrews/population-dynamics-presentation

  Logistic growth is the most natural model for population dynamics

            

 Many variants of Generalized Logistic Growth are widely used (Covid-19 application)

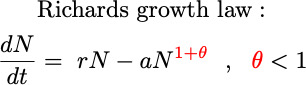
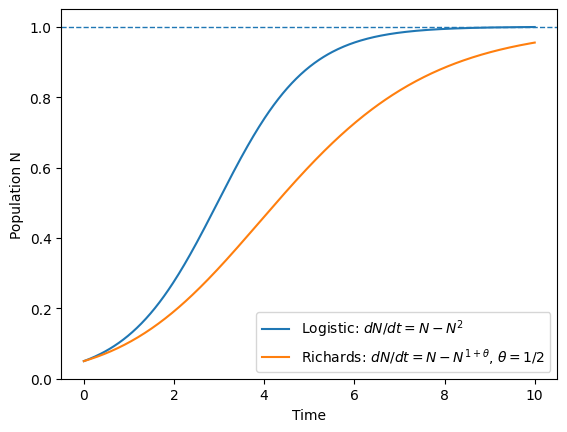
 What can justify a non-analytic growth law, as opposed to higher order analytic terms?

The measured quantity is typically the sum (average) of local populations distributed in space: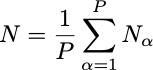   

 Allowing for migration/dispersal/diffusion leads to a set of equations:

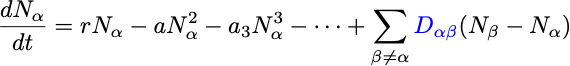
Stochasticity should be important, more so at the local level, sometimes terms

 Seascape                     

        †

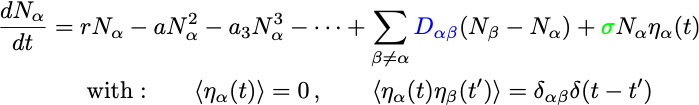 † (Ito interpretation of multiplicative noise)

 Note that seascape noise (spatio-temporal growth fluctuations) is distinct from reproductive stochasticity (demographic noise): 

Next (Mean-field) Outline Growth & saturation Mean field analysis Extinction on a seascape Growth on a seascape Diversity vs Stability Coexistence on a seascape Phase behavior Summary

 Demographic noise leads to extinction via the Directed Percolation universality class  [Janssen+Tauber (2005), ...]

Including both forms of stochasticity in real space with diffusion leads to:

  †

The linear version (a=0) describes the evolving weight of directed polymers in random media (in the KPZ universality class).

[Tu+Grinstein+Munoz (1997); Munoz+Hwa (1998); ...]