Growth on a seascape
![]() Variations at each node are governed by time-scales from growth, migration, and noise
Variations at each node are governed by time-scales from growth, migration, and noise

However, variations of the mean
take the simpler form
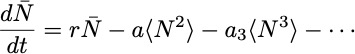
Assuming that the growth rate is always sufficiently slow to allow for a quasi-static state, such that
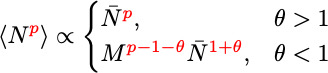 ,
,
provides a route to obtain the empirical Richards growth equation for sufficiently strong seascape stochasticity
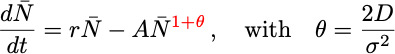
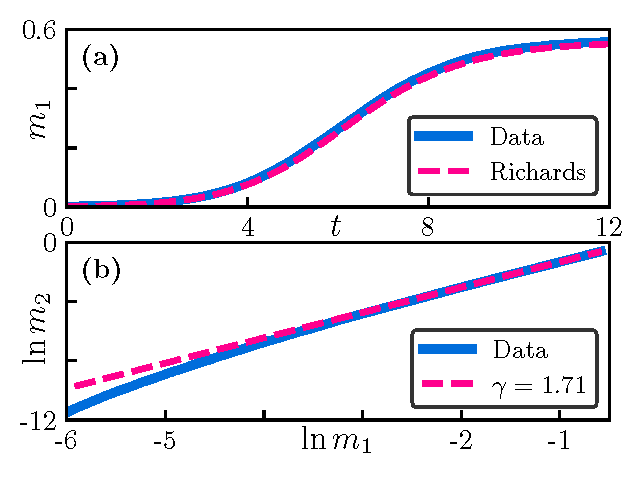
Numerical simulations [D. Swartz, B. Ottino-Loffler, M. Kardar, PRE 105, 014417 (2022)] support this conclusion
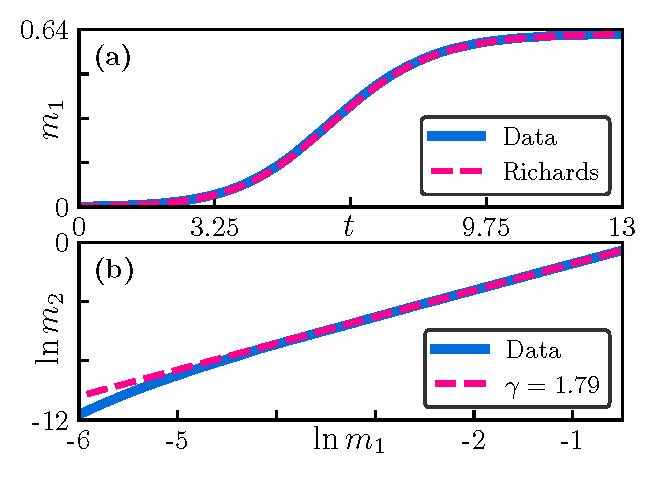
![]() The anomalous scaling of population variance with mean is known in ecology as
The anomalous scaling of population variance with mean is known in ecology as
relating the scaling of variance of population to its mean (in space of time).
A potentially testable link between local population distributions, and a global growth exponent.
![]() Numerical simulation of time evolution of the population density
Numerical simulation of time evolution of the population density
![]() Results of numerical simulations in one dimension:
Results of numerical simulations in one dimension:
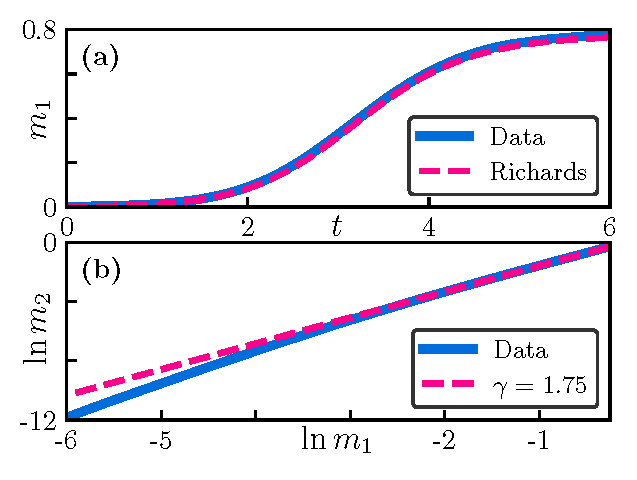
and two dimensions: