Research
Solving Eigenproblems with Approximate Constraints or Symmetries
Unlike in classical mechanics, quantum systems often have a discrete set of possible states, such as the "s", "d", "p", or "f" orbitals in an atom. To understand a quantum system, then, the goal is to find and characterize all of these states. But in many problems, we aren't actually interested in all of the possible states; we want to find states that satisfy certain criteria. For instance, if we want to understand how an electron scatters off a nucleus, we need to identify the quantum states that travel outward from the nucleus as waves. If we want to understand how a given electronic state responds to a local defect in a crystal, we want to find the quantum states that resemble our known solution away from the defect.
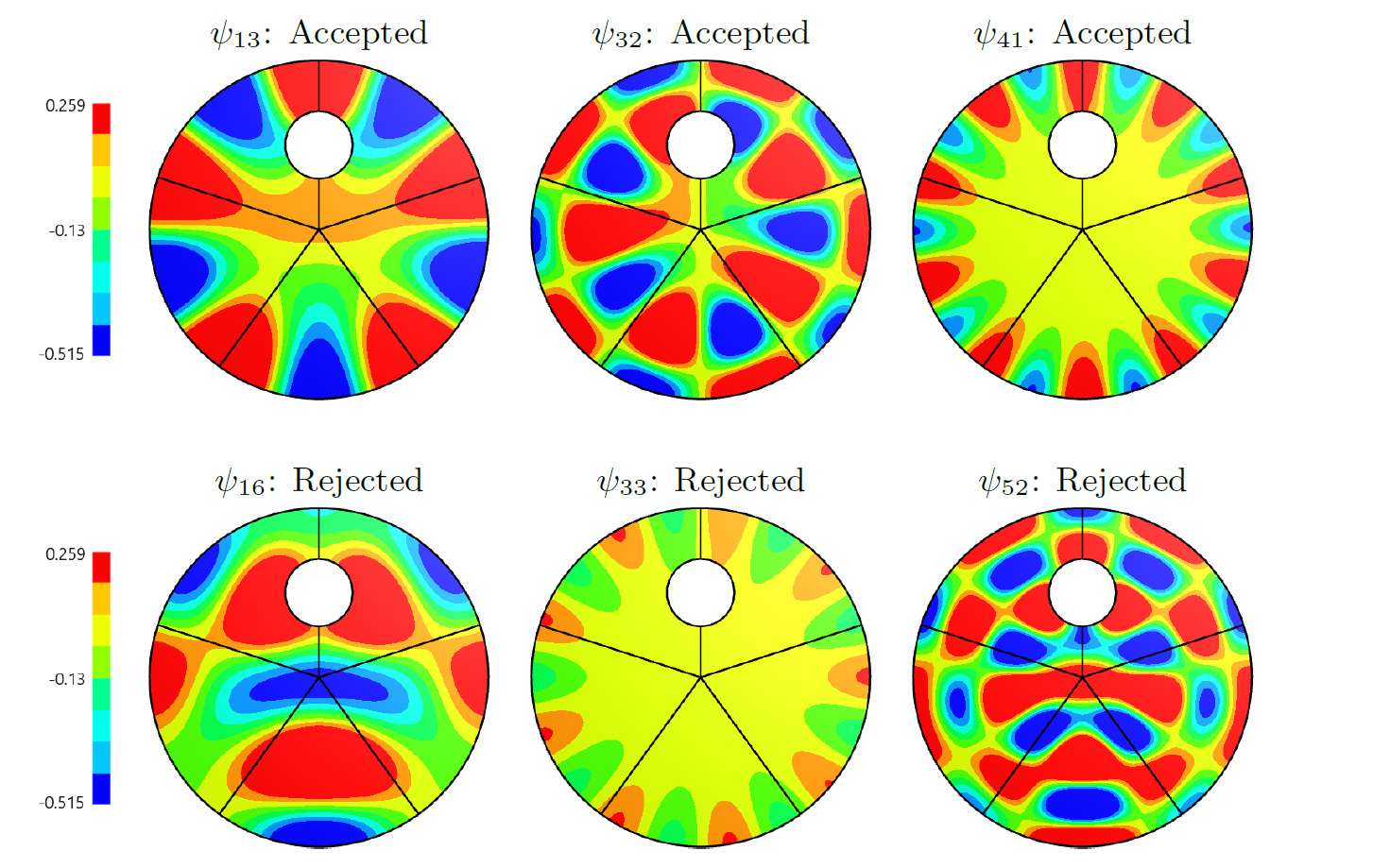
We have employed our algorithm here to identify eigenstates of the Laplacian that approximately carry a five-point symmetry. Our algorithm returns the top three states shown, but not the bottom three.
These problems – and many others – can be formulated as a certain "eigenproblem" with linear constraints. That is, if we have a Hilbert space, a Hermitian operator on that space, and a closed subspace, can we find all of the eigenvectors of our operator that lie nearby (i.e., within a given tolerance to) the closed subspace? Along with Jeffrey Ovall (Portland State University), I have developed an algorithm to solve this class of problems efficiently, and shown how it applies to a variety of practical scientific problems.
The PQL (Perturbative Quasi-Linear) Model of Stratified Turbulence
Many key fluid flows in nature—including the atmosphere and the deep ocean—are stratified, meaning that their density varies significantly in the vertical direction. However, stratified turbulence gives rise to a separation of scales that precludes traditional methods of simulation, and so large-scale, accurate models of these flows remain outside our reach, even with current technology.
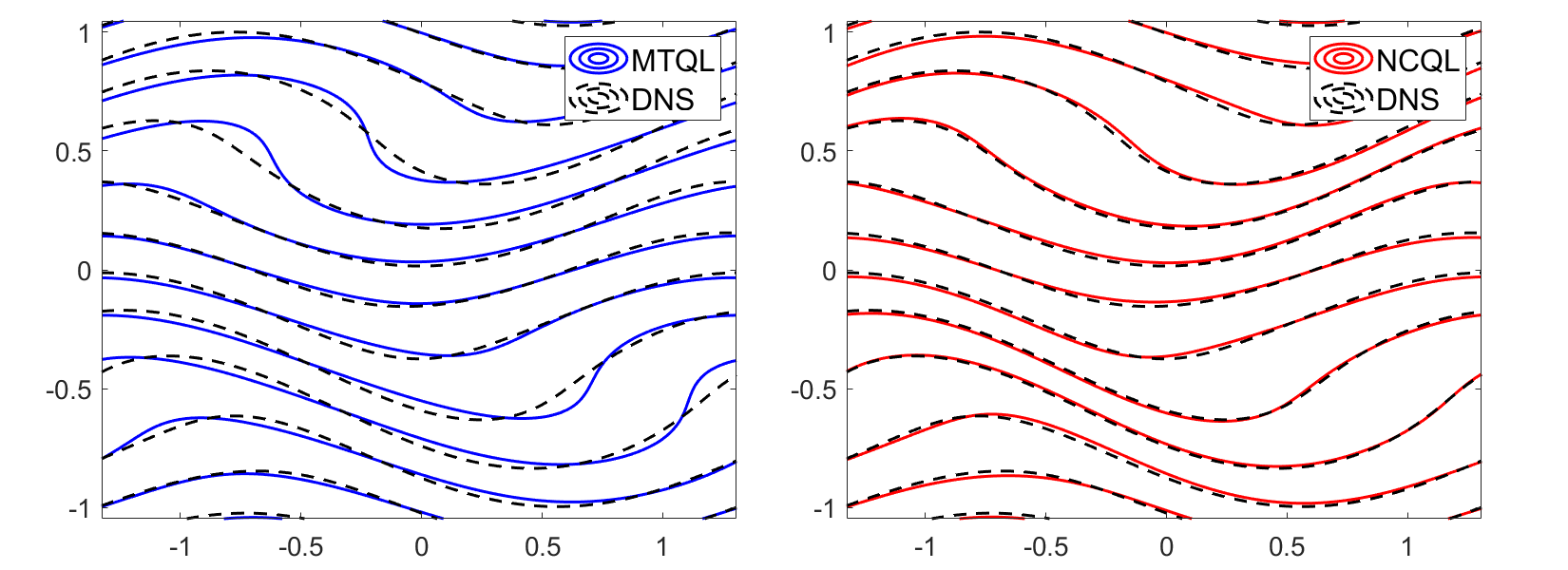
A model flow of Froude number 0.03, Reynolds number 1100; despite the large Reynolds number, the strong stratification here brings the flow to a steady state. Our NCQL algorithm provides a significant improvement over the existing MTQL algorithm for strongly stratified flows.
However, Chini et al. recently developed a "multi-timescale quasi-linear" (MTQL) algorithm to model such flows in the stratified limit; MTQL reduces and splits the Boussinesq system into a mean and fluctuating flow, drastically reducing the computation time needed to model a stratified flow. In my Master's dissertation at Cambridge—and in ongoing work—I have developed an improved, "non-linear cascading quasi-linear" (NCQL) approach to model these flows. Using weakly nonlinear theory, NCQL directly models the forward energy cascade of stratified flows, achieving significant improvements over MTQL in the moderately and highly stratified regimes (pictured above).
Classical Pilot-Waves
A central focus of my work at MIT is the investigation of hydrodynamic quantum analogues, and particularly the "walking" oil droplet system of Couder and Fort. These walking droplets exhibit a wide variety of quantum-like features: stable spin states and quantised orbits, Bohm-like "surreal trajectories", and Fraunhofer-like diffraction patterns, among others.
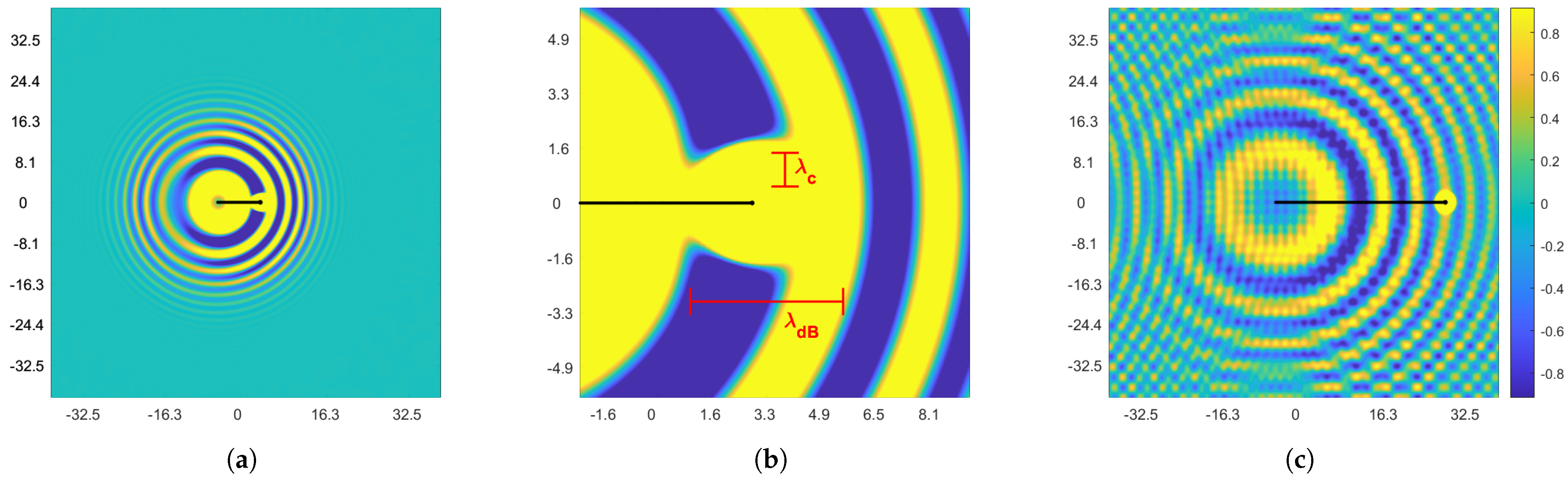
Our new, Lagrangian pilot-wave model is able to reproduce many of the key properties of de Broglie's early "double solution" proposal for quantum mechanics: internal particle oscillations at the Compton scale, the de Broglie momentum-wavevector relations, and de Broglie's "harmony of phases" between the particle and wave.
My work lies on the theoretical end of this project; though these droplets exhibit qualitative similarities to quantum mechanics, they often fall short in achieving quantitative agreement. Through analytical and numerical approaches, I am investigating which quantum phenomena can be closely approximated with techniques of classical field theory.
Capillary Currents, and the Spreading of Viscous Droplets and Puddles

How does a droplet of viscous fluid spread out over a (smooth or rough) solid surface? This question has seen a great deal of attention in both academic and industrial fluid mechanics over the past 100 years, revealing a number of surprising features. For one, the work of Hardy (1919) shows that such a droplet is often preceded by a microscopic "precursor film" of fluid, which facilitates the droplet's spreading dynamics. Later work by Hervet and de Gennes (1984) developed a theoretical model for the spreading of a small* viscous droplet over a precursor film, based on surface tension physics, which rationalized the data collected by Hoffman (1975) and recontextualized several results of Tanner (1979). Large* viscous droplets have also been the focus of recent work, and, so far, have been thought to follow gravity-driven physics entirely distinct from the small droplet case.
[ *For water, "small" means ~1mm or smaller. "Large" means ~1cm or larger ]
In my work, I have developed a new, unified model for viscous droplets and puddles of all scales. Much like the model of Hervet and de Gennes, we propose that such droplets evolve in a "quasi-equilibrium" manner, always maintaining a balance between gravity and surface tension. This balance is broken only by the tension force at the "contact line" (where the droplet meets the surface), which stretches it out slowly; the stretching rate is determined by an energy balance, based on the idea that energy is dissipated throughout the entire bulk of the droplet. The new model adjusts and greatly simplifies the original description of Hervet and de Gennes for small droplets, and it offers a new, self-consistent explanation for the observed spreading of large droplets.

To validate the new model of droplet spreading, Lucas Warwaruk (MIT MechE) has performed a series of experiments investigating the spreading of silicone oil over roughened glass surfaces. Our model can be distinguished from the previous, gravity-driven hypothesis by looking at how the precursor film spreads. The data for the droplet radius R1 and the precursor film radius R2 closely conform to our predictions, validating our model more generally.
Moving beyond circular droplets, I have used the new model to show that viscous puddles spread out according to a novel "geometric flow". Namely, the future shape of a puddle can be determined by looking only at the shape of its contact line, regardless of puddle depth, volume, or chemistry:
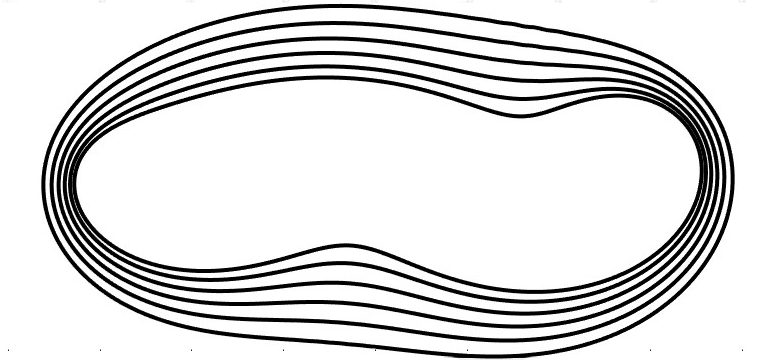
An example of a puddle spreading outward under my new "capillary current" model. To simulate the spreading of a puddle, I have introduced a simple "AAA-Helmholtz" algorithm to solve the (modified) Helmholtz problem in a time-evolving domain. Helmholtz problems arise in a variety of important scientific (and in particular, fluid mechanical!) applications.
A Spectral Theory of Scalar Volterra Equations
Volterra integral and integro-differential equations have been the subject of much study, from the perspective of both pure mathematics and applied science. In one direction, developments in analysis (both classical and recent) have yielded far-ranging existence, uniqueness, and spectral results for such equations. In the other, applications in electrical engineering, materials science, and other fields of science have inspired a substantial library of techniques with which to work with such equations in practice.
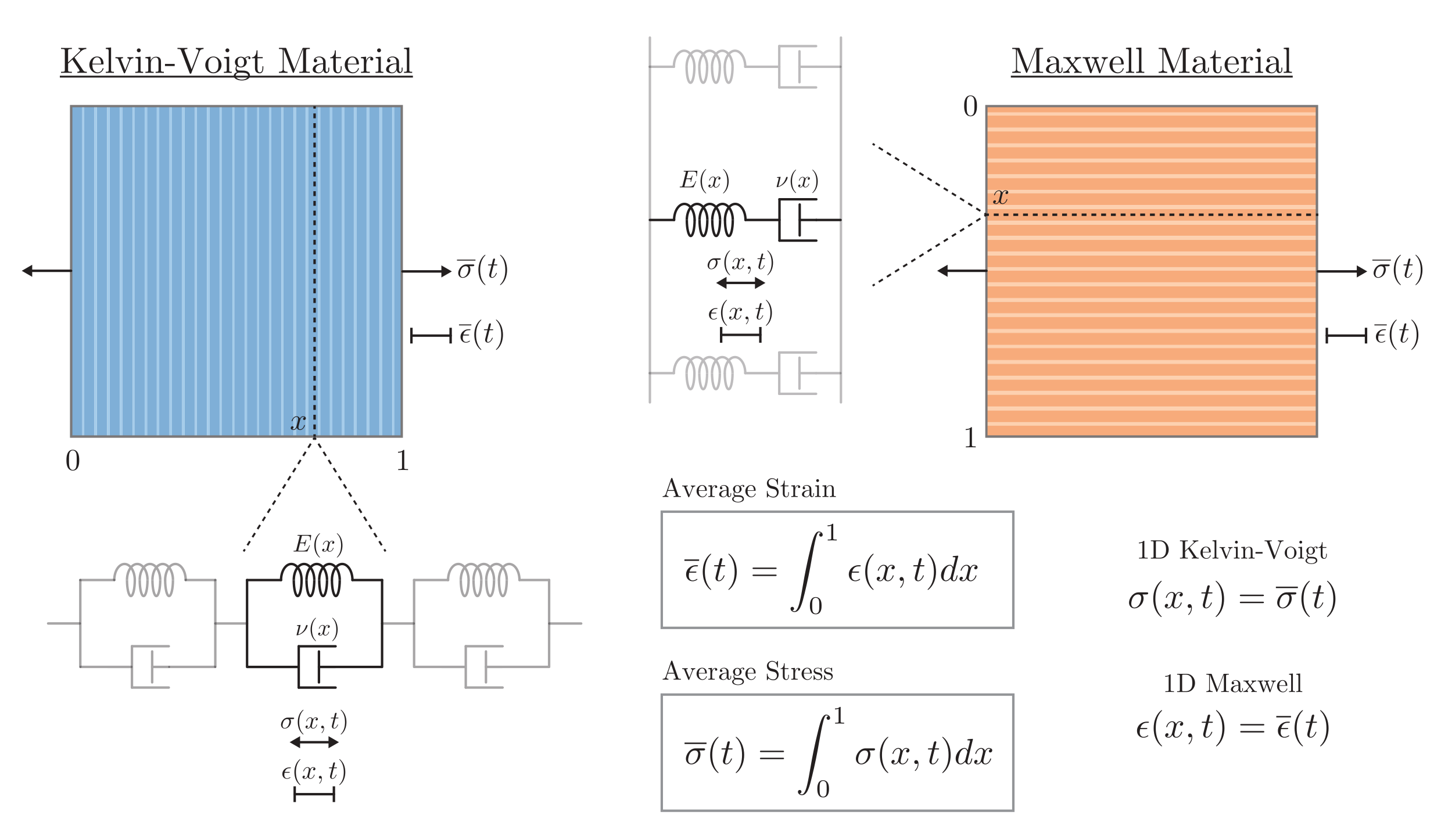
The stress and strain across a 1-D viscoelastic material can be related by a Volterra integral equation, which depends on the properties of the material. Such integral equations always carry "completely monotone" integral kernels, and thus fall within the scope of our general theory.
In my recent work with George Stepaniants (CalTech), we have attempted to bridge the gap between theory and application in the study of scalar, linear Volterra equations. As a starting point, we developed a system of correspondences between five major classes of Volterra equations: integral and integro-differential equations with completely monotone (CM) integral kernels, corresponding to linear viscoelastic models; those with positive definite (PD) integral kernels, corresponding to partially-observed quantum systems; discrete-time Volterra equations with PD kernels; delay differential equations of a generalized PD type; and a generalized class of fractional differential equations.
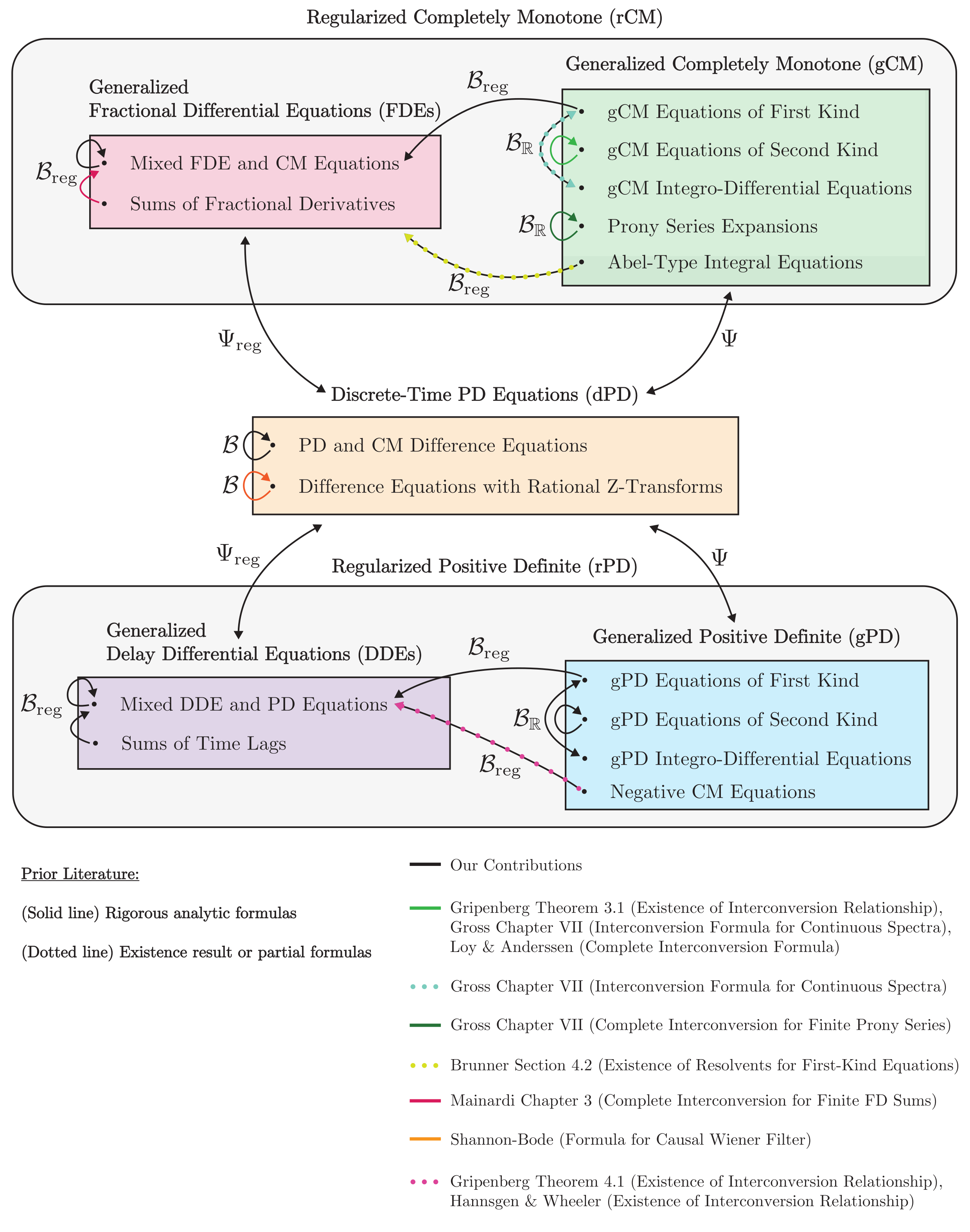
Our system of correspondences between the five core classes of Volterra equations under consideration. We have indicated where existing literature has partially or completely treated subclasses of Volterra equations.
In doing so, we have shown that all five classes can be reduced to a single, powerful spectral theory. We have leveraged this theory to recover practical, closed-form solutions of all five classes, and we showed that interconversion yields a natural, continuous involution within each class. Particularly in the most challenging limits—including first-type integral equations and fractional and delay differential equations—this theory yields a plethora of novel formulas for their analytical solutions, as well as substantial insight into their behavior. Our work also unifies, extends, and rigorously grounds (when applicable) several existing results from applied science: interconversion formulas in viscoelasticity, certain spectral formulas in operator theory, classical formulas for finite Prony series and fractional differential equations, and convergence of Prony series to CM kernels, among other results. Finally, our theory yields a novel, geometric construction of the regularized Hilbert transform, extends it to a wide class of infinite measures, and reveals a natural connection to delay and fractional differential equations.
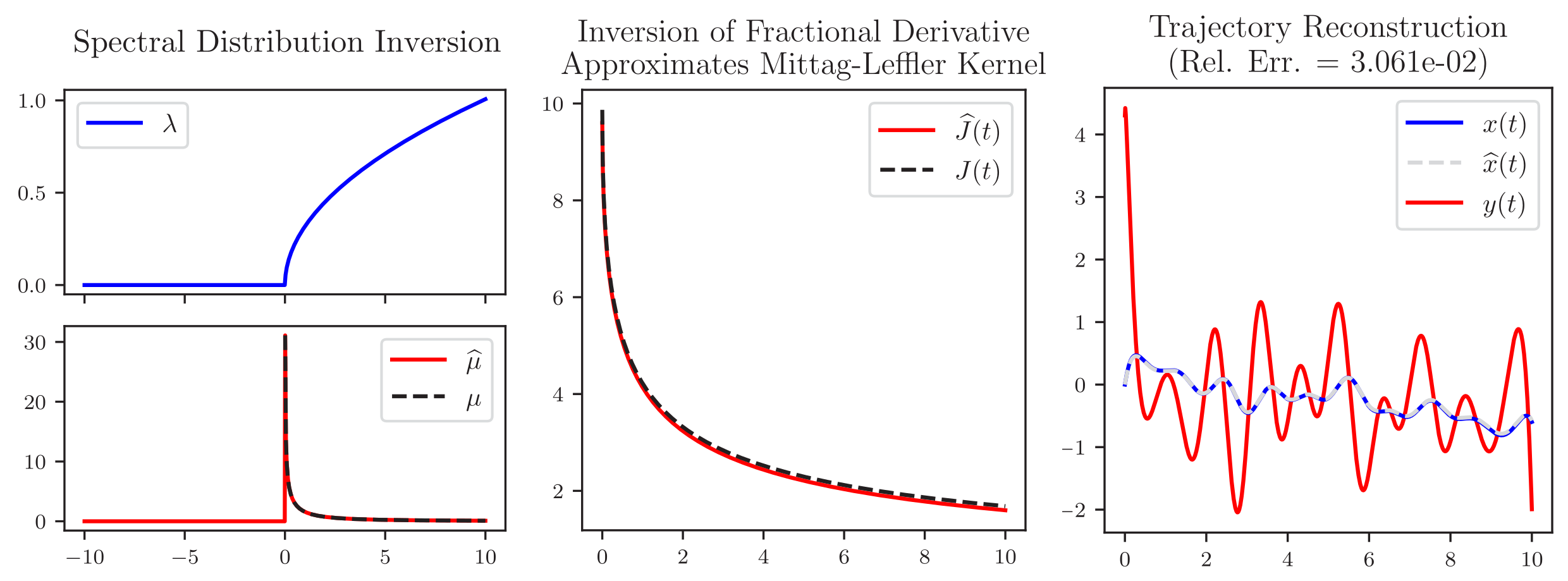
Our theory allows for efficient, closed-form solution to several wide classes of Volterra equations, including those with fractional derivatives. Here, we see that our approach recovers the classical result in the case of a simple fractional differential equation.
Our work also offers a substantial, practical toolbox with which to study and solve such equations. On one hand, it reduces simple Volterra equations to pen-and-paper calculations and offers significant analytical insight in more complicated examples. On the other, by connecting our theory with the AAA approximation scheme of Nakatsukasa et al. (2016), we have introduced a powerful, spectral method for working with scalar Volterra equations numerically.



