Surface integral

Say we have a surface $S$ in $\mathbb R^3$ and a scalar field $f : \mathbb R^3 \to \mathbb R$. We want to integrate $f$ over the surface $S$.

Here $dA$ is the differential surface area.

Since we are integrating a 2 dimensional surface in 3 dimensional space, let’s parametrize $S$ with a function $\mathbf r(u, v) : \mathbb \Omega \to \mathbb R^3$. $\mathbf r$ takes a point in the region $\Omega$ of the $(u, v)$ plane and projects it onto the 3 dimensional surface $S$.

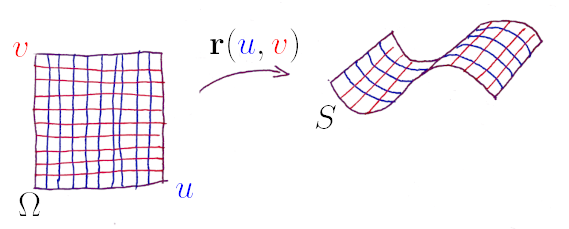
Imagine breaking up $\Omega$ into square pieces, each of some area $\Delta A = \Delta u \times \Delta v$. When the corresponding region is projected onto $S$, the area is distorted. If we hold one variable (say, $u$) constant and vary the other one by some small $dv$ we will get a small vector that we will call $\mathbf r_v dv$. Likewise, for a small change $du$ we get $\mathbf r_u du$. These two vectors form a parallelogram in $\mathbb R^3$. The area on $S$ that corresponds to our differential area $du \times dv$ on $\Omega$ is then the area of the parallelogram formed by the two vectors $\mathbf r_u du$ and $\mathbf r_v dv$. Recall that the magnitude of the cross product of two vectors is the area of the parallelogram they form, so we can write this are as $dA = \lVert \mathbf r_u \times \mathbf r_v \rVert du dv$.

We can now write our integral in terms of $\Omega$ and $\mathbf r$:

Over a vector field

The integral we just discussed was over a scalar field $f$, but we can just as easily compute one for $\mathbf F: \R^3 \to \R^3$. In this case, we want to integrate the dot product of $\mathbf F$ with the outwards pointing normal vector $\hat{\mathbf n}$.

Note that since $\hat{\mathbf n}$ is normal to the surface, it must be perpendicular to both $\mathbf r_u$ and $\mathbf r_v$. Therefore the direction of $\hat{\mathbf n}$ is just the cross product $\mathbf r_u \times \mathbf r_v$. Since $\hat{\mathbf n}$ is a unit vector, we need to divide by the norm, finally giving us $\hat{\mathbf n} = \frac{\mathbf r_u \times \mathbf r_v}{\lVert \mathbf r_u \times \mathbf r_v \rVert}$.

Now we can set $f=\mathbf F \cdot \hat{\mathbf n}$ and use the surface integral formula above.