A/C circuits with resistors, inductors, and capacitors

Consider a circuit consisting of an alternating voltage source, a resistor, inductor, and capacitor in series. In general for these types of circuits we are usually given the voltage and are looking for the current as a function of time.

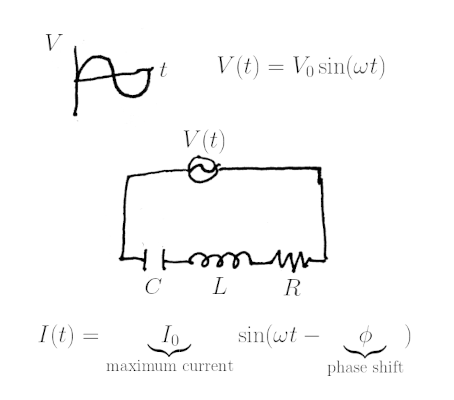
The circuit diagram above shows a typical A/C RLC circuit and the general form for the current $I(t) = I_0 \sin(\omega t - \phi)$.

Resistor

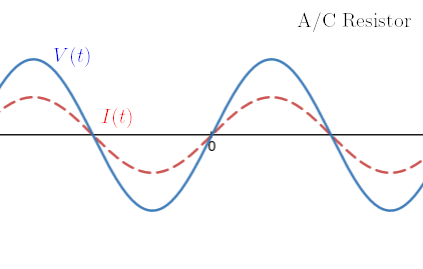
A resistors behavior is defined by the equation $V_R = I_R R$. Substituting the voltage and current we get $V_0 \sin(\omega t) = I_0 R \sin(\omega t - \phi)$. We see that $I_0 = \frac{V_0}{R}$ and $\phi = 0$. Since the phase shift is zero, this means that the current through a resistor is in phase with the voltage across it.

Inductor

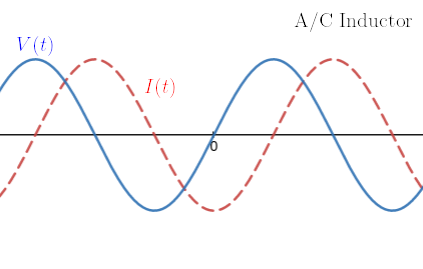
An inductor is defined by $V_L = - L \frac{dI_L}{dt}$. Substituting in the given voltage, we see that $I_L \propto -\cos(\omega t)$, since its derivative must be proportional to $\sin(\omega t)$. Evaluating we find that $I_0 = \frac{V_0}{\omega L}$ and $\phi = \frac{\pi}{2}$. Since the phase shift is positive, the current through an inductor lags the voltage across it.

Capacitor

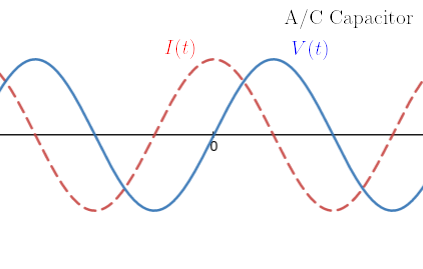
A capacitor is defined by $Q=CV_C$. Differentiating, we find $I_C = C \frac{dV_C}{dt}$. Here the current is proportional to the derivative of voltage, so $I_C \propto \cos(\omega t)$. Evaluating we find that $I_0 = \frac{1}{\omega C}$ and $\phi = -\frac{\pi}{2}$. This time the phase shift is negative, so the current through a capacitor leads the voltage across it.

General solution

For an A/C RLC circuit in series, we can find the general solution for current using impedance. The total impedance is:

And the total phase shift is:

Putting this together, we get: