The Root Locus Rules
To assist in the construction of root locus plots, the `` Root
Locus Rules'' for plotting the loci are summarized here. These rules
are not universal, and every author has his own favorite set and
ordering of the rules. In his landmark textbook, Walter
Evans lists approximately ten rules, but does not
order or number them [1, Appendix B], while
Roberge enumerates eight rules
[9, pages 121-126].
All root locus rules can be directly traced to the characteristic
equation, 1+L(s)=0. If we assume that the loop transfer function can
be written as
L(s)=KL0(s), where K is a positive gain, then we can
write the magnitude condition and the angle condition as
|L(s)|=|KL0(s)|=1
We assume that the loop transfer function has P open loop poles and Z
open loop zeros, and that there are at least as many poles as zeros
(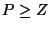 ).
).
- Rule 1
- The number of branches, which are the paths of the closed-loop poles, is
equal to the number of open-loop poles, P.
- Rule 2
- The branches start at the open-loop poles and end at the open-loop
zeros. In addition to the Z explicit open-loop zeros in the
transfer function, there are P-Z open-loop zeros at infinity.
- Rule 3
- Branches of the root locus lie on the real axis to the left of an odd
number of poles and zeros. Complex-conjugate pairs of poles and zeros
are not counted, since they contribute no net angle to the real axis.
- Rule 4
- If a branch on the real axis lies between a pair of poles, the root
locus must break away from the real axis somewhere between the poles.
Similarly, if a branch on the real axis lies between a pair of zeros,
there must be an entry point between that pair of zeros.
- Rule 5
- As K gets very large, P-Z branches go to infinity. These branches
approach asymptotes at angles to the real axis of
where
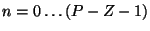 and the centroid of these asymptotes is on the
real axis at
and the centroid of these asymptotes is on the
real axis at
- Rule 6
- The departure angles of the branches from an
mth-order pole on the real axis are
if the mth-order pole is to the left of a even number of poles and
zeros. If the mth-order pole is to the left of a odd number of
poles and zeros, then the departure angles are
- Rule 7
- If there are two or more excess poles than zeros (
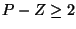 ), then
for any gain K, the sum of the real parts of the closed-loop poles (or
the average distance from the
), then
for any gain K, the sum of the real parts of the closed-loop poles (or
the average distance from the 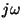 -axis) is constant3.
-axis) is constant3.
- Rule 8
- Ignore remote poles and zeros when considering the root locus near the
origin of the s-plane, and combine the poles and zeros near the
origin when considering the root locus for remote poles and zeros.
- Rule 9
- The departure angle from a complex-conjugate pole can be found by
considering the angle condition on a small circle around the pole.
The result is found by summing all the angles from open-loop zeros
and subtracting all the angles from all other poles
The approach angle to a complex-conjugate zero follows similarly
This sum only needs to be calculated once for each complex pair, since
the root-locus diagram is symmetric above and below the real axis.
- Rule 10
- The break-away (entry) points from (to) the real axis between a pair
of poles (zeros) can be found either by geometric
construction4 or by finding the
local maxima (minima) of the gain function
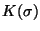 ,
solving
,
solving
Fortunately, this level of accuracy is rarely necessary.
Kent H Lundberg
2002-11-14