A paradox of existence[1]
draft of November 8, 1998
S. Yablo
It seems to me very curious that language should have grown up as if it were expressly designed to mislead philosophers; and I do not know why it should have. -- GE Moore to IA Richards
I. Introduction
About a half a century ago, Quine established to most people's satisfaction that the argument for abstract objects, if there was going to be one, would have to be a posteriori in nature. And it would have to an a posteriori argument of a particular sort: an indispensability argument representing numbers, to use that example, as entities that "total science" cannot do without.[2]
This is not to say that a priori arguments are no longer attempted; they are, for instance by Alvin Plantinga in The Ontological Argument , and Crispin Wright in Frege and the Conception of Numbers as Objects . But such arguments carry with them a palpable sense of daring and a distinct feeling of pulling a rabbit out of a hat. Nobody supposes that there are easy proofs, from a priori or empirically obvious premises, of the existence of abstracta.[3] (The only easy existence proof we know of in philosophy is Descartes's cogito.)
The paradox is that, if we are to go by what philosophers say in other contexts, such bashfulness is quite unnecessary. Abstract objects are a priori deducible from (i) a priori premises and/or (ii) obvious, uncontroversial empirical facts.
EXAMPLE i . As everyone knows, an argument is valid iff every model of its premises is a model of its conclusions. I have never seen empirical evidence offered for this equivalence so I assume the knowledge is a priori. On the other hand, it is also (often) known a priori that such and such an argument is invalid. From these two pieces of a priori knowledge it follows by modus ponens that there exist certain abstract objects, viz. models.
EXAMPLE ii.. It is a priori, I assume, since observational evidence is never given, that there are as many Fs as Gs iff there is a one to one function from the Fs to the Gs. It is also known, a posteriori this time, that I have as many left shoes as right. From these two pieces of information it follows by modus ponens that there exist functions.
II. Platonic objects
So far, so bad. But there is more to the difficulty than we have yet appreciated. This is because objects that are not abstract, or not obviously so, can be similarly "deduced" on the basis of a priori-looking bridge principles. I have in mind principles like "it is possible that B iff there is a B-world," and "Jones buttered the toast F-ly iff there was a buttering of the toast by Jones and it was F," and "Jones is human iff the property of being human is possessed by Jones." That non-abstract objects appear also to admit of "overeasy" proof shows that we still have not got an exact bead on the intended paradox.
Suppose we try again. There is a widespread practice in philosophy of discovering unexpected objects in truth-conditions, that is, of discerning whatsits in the truth-conditions of statements that are not on the face of it about whatsits. So,
|
the truth-value of |
is held to turn on |
|
"argument A is valid" |
the existence of countermodels |
|
"it is possible that B" |
the existence of worlds |
|
"there are as many Cs as Ds" |
the existence of 1-1 functions |
|
"there are over five Es" |
the number of Es' exceeding five |
|
"they did it Fly" |
the event of their doing it being F |
|
"there are Gs which BLAH" |
there being a set of Gs which BLAH |
|
"she is H" |
her relation to the property H-ness |
Objects with a tendency to turn up unexpected in truth-conditions like this can be called platonic . Models, worlds, properties, and so on, are platonic, relative to the areas of discourse on the left, because the sentences on the left aren't intuitively about models, worlds, and properties. An example of non-platonicness might be people considered in relation to population discourse. That the truth about which regions are populated should hinge on where the people are does not make anything platonic, because people are what population-discourse is visibly and unsurprisingly all about.
Where are we? Objects are platonic relative to an area of discourse due to the combination of something positive -- the discourse depends for its truth-value on how objects like that behave -- with something negative -- the discourse is not about objects of that type. It appears to be this combination, truth-dependence without aboutness, that makes for the paradoxical result; it appears, in other words, that with all platonic objects, abstract or not, there is going to the possibility of an overeasy existence proof. Just as functions can be deduced from the premise that I have as many left hands as right ones, events can be conjured a priori out of the fact that Jones buttered the toast slowly, and worlds out of the fact that she could have done it quickly.
III. Quine's way or the highway
The paradox is now shaping up as follows. Let X be whatever sort of platonic object you like: numbers, properties, worlds, sets, it doesn't matter. Then on the one hand you've got
Quineanism:to establish the existence of Xs takes a holistic a posteriori indispensability argument;
while on the other hand you've got
Rationalism:the existence of Xs follows by "truths of reason" -- a priori bridge principles - from a priori &/or empirical banalities.
The reason this is a paradox and not merely a contradiction is that Quineanism is received opinion in philosophy, while Rationalism is a straightforward consequence of received opinion, viz., the opinion that we are capable in some cases of a priori insight into truth-conditions, and can a priori "see" that an argument is valid iff it has no countermodels, that it is possible that S iff an S-world exists, and so on.
What is to be done? One option is of course to embrace Rationalism and admit that the proof of numbers and the rest is easier than anyone had imagined. I am going to assume without argument that such a course is out of the question. Our feeling of hocus-pocus about the "easy" proof of numbers (etc.) is really very strong and has got to be respected.
If that is right, then only one option remains: we have to renounce our claim to knowing the bridge principles priori. Perhaps the principles are false, as John Etchemendy maintains about the Tarskian validity principle.[4] More likely our justification for them is not a priori; the Tarski principle owes its plausibility to the prior hypothesis that there are sets, and the argument for them is experiential and holistic. The point either way is that we have to stop carrying on as though it is known independently of experience that, e.g., the valid arguments are the ones without countermodels.
If only it were that easy! The trouble is that our rights of access to the bridge principles do not seem to be hostage to empirical fortune in the way suggested; our practice with the principles does not feel like it is "hanging by a thread" until the empirical situation sorts itself out. This shows up in a couple of ways, one having to do with our actual attitudes and another having to do with the attitudes we would have had in certain counterfactual situations.
Actual:: Many or most of us using the Tarski biconditional have no particular view about abstract ontology; certainly we are not committed platonists. If the biconditional (as employed by us) truly presupposed such an ontology, then weought to feel as though they were walking on very thin ice indeed. I don't know about you but I have never, not once, heard any anxieties expressed on this score.
Counterfactual: Also testifying to our (surprising) insouciance about the true ontological situation is the "hypothetical" fact that if someone were to turn up with evidence that abstract objects did not exist, our use of models to figure validity would not be altered one iota. Burgess & Rosen begin their book A Subject with No Object with a relevant fable:
Finally, after years of waiting, it is your turn to put a question to the Oracle of Philosophy...you humbly approach and ask the question that has been consuming you for as long as you can remember: 'Tell me, O Oracle, what there is. What sorts of things exist?' To this the Oracle responds: 'What? You want the whole list? ...I will tell you this: everything there is is concrete; nothing there is is abstract....' (1997, 3)
Suppose we continue the fable a little. Impressed with what the Oracle has told you, you return to civilization to spread the concrete gospel. Your first stop is at [your school here] where researchers are confidently reckoning validity by way of calculations on models. You demand that the practice be stopped at once. It's true that the Oracle has been known to speak in riddles; but there is now a well-enough justified worry about the existence of models that all theoretical reliance on them should cease. They of course tell you to bug off and am-scray. Which come to think of it is exactly what you yourself would do, if the situation were reversed.
IV. Impatience
Our question really boils down to this: What is the source of the impatience we feel with the meddling ontologist -- the one who insists that the practice of judging validity by use of Tarski be put on hold until the all-important matter is settled of whether models really exist?
One explanation can be ruled out immediately: we think the principles would still hold (literally) true whether the objects existed or not.[5] That would be to think that if, contrary to what we perhaps suppose, there are no models, then every argument is valid! Likewise if the models are found to peter out above a certain finite cardinality -- not for deep conceptual reasons, mind you, but as a matter of brute empirical fact -- then a whole bunch of statements we now regard as logically contingent, such as "there are fifty zillion objects," are in fact logically false. If as seems clear we are not in the market for this sort of result, then we can draw the following moral:
Ontology Matters to Truth: Our complacency about the bridge principles is not due to a belief that they hold literally true regardless of the ontological facts. (It can't be, since we have no such belief.)
A second explanation of our impatience seems equally misguided: we are confident that the negative empirical findings will never be made. It may be that we are confident of this; it is not as though any great number of ontological controversies have been resolved by empirical means in the past. Even if it is granted, though, that we do not expect evidence to turn up that casts doubt on the existence of models, why should that prevent us from having a view about what to say if it did? After all, I take it we are also confident that it will never be discovered that there are no people. Nevertheless, it seems clearly true that if the Oracle convinces us that people are an illusion, we will conclude via principle (R) that no region is populated; and clearly false that if the Oracle convinces us that there are no models, we will conclude that all arguments are valid. I conclude that
Experience Matters to Ontology: Our complacency about the bridge principles is not due to a belief that the trouble-making empirical facts will never come to light. That belief may be there, but our complacency runs deeper than it can explain.
The upshot of these two morals is that it does not really solve the paradox to say that Quineanism wins out over Rationalism. If experience matters to ontology, and ontology matters to truth, then experience ought to matter to truth as well. How is it then that the bridge principles are treated, and apparently rightly treated, as experience-independent? What accounts for the a priori-like deference we pay to them? How can we feel justified in ignoring a kind of evidence that would, by our own lights, exhibit our belief as false?[6]
Here is the only way out I can see: What entitles us to our indifference about evidence that would exhibit the principles as false is that we were never committed in the first place to their truth..[7] Our attitude towards them is attitude A, and attitude A leaves it open whether the alluded-to objects really exist.
V. Platonism as the price of access
Attitude A remains of course to be identified. First, though, we need to consider some reasons for insisting (against what has just been said) that the bridge principles are in fact true. Take again Tarski's validity principle
(V) an argument is valid iff it has no countermodels.
One obvious thought is that if (V) were not true, then we would not be able touse in the ways we routinely do. The point of the "iff" is to give us license to infer back and forth between the left and the right hand sides. Discovering that the right hand side is true, or false, we can conclude that the left hand side is true, or false; and vice versa. If these inferences require us to regard (V) as true, then that is a powerful reason so to regard it.
Humor me for a minute while I state the case a little more guardedly: The back and forth inferences give us reason to regard (V) as true if they are inferences that people actually perform.
Well, aren't they? You find a countermodel, you conclude that the argument is invalid. You show that there are no countermodels, you conclude that the argument is valid.
I wonder whether that is a fair description of what really goes on. If you're anything like me, the activity you call "finding a countermodel" really just consists in describing to yourself what the countermodel would have to be like; it consists in laying out a blueprint for a structureof the appropriate sort. The issue of whether anything indeed answers to the blueprint is not taken up and indeed seems rather beside the point.
As for the other direction, where countermodels cannot be found and we judge the argument to be valid, again, the activity of "finding that there are no countermodels" is misdescribed. The fact that one is really relying on in judging validity is not that countermodels fail to exist -- that you could have learned from the oracle, and it would not have altered your validity-judgments one iota -- but that there's something in the very notion of a countermodel to argument A that prevents there from being such a thing. A consistent blueprint can't be drawn up because the conditions such a model would have to meet are directly at odds with each other. Once again, the issue of whether models do or do not really exist is not broached and seems of no genuine relevance.
So: if you look at the way the Tarski biconditional is actually used, any larger issue of the existence of models "in general" is bracketed. It's almost as though we were understanding (V) as
(V*) an argument A is valid iff - ontological worries to the side, that is, assuming that models as a general category exist -- A has no countermodels. [8]
The idea that (V) is in practice understood along the lines of (V*) has the added virtue of explaining our impatience with the ontologist's meddling. If the issue is whether there are countermodels assuming models, it really doesn't matter whether models exist. The truth value of this claim:
(a*) assuming that models exist, the argument has a countermodel,
is entirely independent of the truth value of this one:
(b) models exist.
Of course, the question will be raised of why someone would utter (V) when what they really literally meant was (V*). Suffice it to say that linguistic indirection of this sort is not unknown; details will be given below. Right now let's look at some other reasons why a literal interpretation of the bridge principles might seem unavoidable.
VI Platonism as the key to clarity
A great goal of analytic philosophy is to make our ideas clear. This goal is not often achieved to the community's satisfaction, but in a few instances there has been undeniable progress. Everyone will agree, I think, that our notion of cardinality -- especially infinite cardinality -- was made clearer by Cantor's explanation in terms of 1-1 functions; that the notion of inductive definability was clarified by Tarski's device of quantifying over all sets meeting certain closure conditions; that our notion of validity was clarified by the appeal to models; and that our notion of continuity is clearer thanks to the epsilon-delta story.
This gives us a second reason for insisting on the reality of platonic objects: if quantifying over functions, models, sets, etc. enables us to clarify our ideas, and clarification of ideas is a principal goal of analytic philosophy, how can we as analytic philosophers be expected to eschew such quantification and the ontological commitment it carries?
It helps to look at a particular example: the controversy sparked early in this century by C.I. Lewis's work in modal logic. Lewis distinguished a number of logical systems differing in their attitude towards formulas like
(a) nec(S)-->nec(nec(S)),
(b) pos(nec(S))-->S,
(c) pos(S)-->nec(pos(S)), ....
His commentators wondered whether competing intuitions about these systems might not be based in subtly dissimilar ideas of necessity and possibility. The breakthrough came of course with the advent of possible worlds semantics. Acceptance of (a) could now be linked with a transitive conception of relative possibility: a world w' that would have been possible, had possible world w obtained, is possible. (Likewise, mutatis mutandis, for (b) and (c).) The benefits were and remain substantial: fewer spurious ("merely conceptual") disagreements, improved self-understanding, fewer fallacies of equivocation, a clearer picture of why modal principles fall into natural packages, and so on.
And now the platonist can argue like: If the clarification that confers these benefits requires us to treat modal operators as (disguised) quantifiers over worlds, then that is how we have to treat them; and that means believing in the worlds.
Isn't there something strange about this line of argument? One normally thinks of clarification as more of a cognitive notion than an ontological one; my goal as a clarifier is to elucidate the content of an idea so that it will be easier to tell apart from other ideas with which it might otherwise get confused. But then, how well I have succeeded ought not to depend on ontological matters except to the extent that the content of my idea exhibits a similar dependence.
With some ideas - "externalist" ideas -- this condition might indeed be met. There may be no way for me to make my idea of water, or of Hilary Clinton, fully clear without bringing in actual water, or actual Hilary Clinton.[9] But my ideas of validity and possibility do not appear to be externalistic in this way. It therefore seems strange to suppose that actual models and worlds would have to be appealed to to make them fully clear, and, related to this, strange to suppose that models and worlds would have to exist for them to be fully clear.
You can guess where this is heading. The clarificatory powers of platonic objects are not to be doubted; but they do not depend on the objects' actually existing. I can do just as good a job of elucidating (to myself and others) my modal concepts by saying
supposing for a moment that necessity is truth at all relatively possible worlds, my concept is one that calls for a transitive relative possibility relation
as I can by saying:
according to my concept of necessity, necessity is truth at all relatively possible worlds, where relative possibility is a transitive relation
Along one dimension, I can do a better job. Suppose I explain my concept of possibility in the second, realistic, way. Then it flows from my concept that if Lewis et al are wrong and there are no counterfactual worlds, then whatever is the case is necessarily the case. This is just false of my concept, and I venture to guess of yours as well. An explication generating false conclusions about a concept's application-conditions is to that extent less accurate and revealing than one that avoids the false conclusions.[10]
VII Platonism and proof
A third way in which people appeal to principle (V) is in metalogical proofs. How are we to show that validity has, for instance, the monotonicity property -- that if P1...Pn/C is valid, then so is P1...PnPn+1/C -- without quantifying over models?[11] Given the models we can do it like so:
(i) An argument is valid iff every model of its premises satisfies its conclusion. (This is (V).)
(ii) If every model of P1...Pn satisfies C then every model of P1...PnPn+1 satisfies C. (By logic and definitions.)
(iii) If P1...Pn/C is valid, then P1...PnPn+1/C is valid. (From (i) and (ii).)
No doubt a proof like this accomplishes something, but notice something funny about it. That an expanded premise set continues to entail the old conclusions seems intuitively a more fundamental fact than the Tarski biconditional that the proof relies on. What then is the point of the exercise? The point is not to show that monotonicity holds, since
no one ever doubted it. Nor does the proof do a very good job of explainingwhy it holds. For the fact allegedly being explained -- that adding a premise does not destroy validity -- appears to lie at a deeper level than the logical thesis called in to explain it, viz. the thesis that a property common to everything with such and features is common also to everything with those features and one additional feature.
If the point of the proof is not to show that monotonicity holds, or why it holds, then what does it accomplish for us? One thing it clearly accomplishes is to show that monotonicity "goes with" -- is implicit in -- our (classical) concept of validity, as opposed to, say, the various alternative concepts discussed in the literature on nonmonotonic logic.[12] Because our classical concept goes with quantifiers over models, assuming models; and assuming models, any countermodel to the expanded argument is a countermodel to the original argument as well. The interesting thing is that the proof thus conceived can be carried out using (V*) in place of (V):
(1) An argument is iff, assuming models, models of the premises satisfy the conclusion. (This is (V*).)
(2) Assuming models, models of P1...Pn satisfy C only if models of P1...Pn+1 satisfy C. (Whatever holds by logic and definitions is true-assuming-models.)
(3) Assuming models, models of P1...Pn satisfy C only if assuming models, models of P1...Pn+1 satisfy C. (By (2), since logical consequences of truths-assuming-models are themselves true-assuming-models.)
(4) P1...Pn/C is valid only if P1...Pn+1/C is valid. (From (1) and (3).)
Note that an argument like this is not available to someone Jones whose concept of validity was nonmonotonic. Suppose for instance that Jones is working with the circumscriptive concept, whereby an argument is valid iff any countermodels it may possess have submodels still satisfying the premises that make the conclusion true. Imagine what her version of the argument would have to look like:
(1) An argument is valid iff, assuming models, minimal models of the premises satisfy the conclusion as well.
(2) Assuming models, minimal models of P1...Pn satisfy C only if minimal models of P1...Pn+1 satisfy C.
The attempt breaks down right here: minimal models of P1...Pn may well not be minimal models of P1....Pn+1, so (2) is just false.[13] This illustrates how (1)-(4) style "proofs" can be used to draw out consequences of quantificationally-explicated concepts without for a moment supposing that the entities quantified over constitute the real grounds of the concepts' application.
For a second example, consider the proof that equinumerosity is symmetrical -- that if there are exactly as many Fs as Gs, then there are exactly as many Gs as Fs -- from the fact that inverting a bijection yields another bijection. There might be any number of reasons why conceiving of equinumerosity in terms of bijections, doubts-about-functions-bracketed, is a worthwhile cognitive strategy. But I doubt that we want to see the proof as "showing" - say, to someone who didn't already believe it -- that exactly-as-many-as is symmetrical, for its symmetry seems intuitively more certain the fact about bijections that is appealed to in the proof. Nor does the proof appear to showwhy equinumerosity is symmetrical. If bijections exist, there are going to be lots of them. But then, rather than grounding my fingers' equinumerosity with my toes in the fact that there are all these bijections, it seems preferable to explain the bijections -- their possibility, at least -- in terms of the prior fact that I have as many fingers as toes. That way we explain many facts in terms of one, rather than one in terms of many.
The proof motive for positing platonic objects is not without merit; the proofs that the objects enable really are instructive. When we realize, though, that the fact proved is not quite what we were led to believe -- not that monotonicity holds, or that equinumerosity is symmetrical, but that these results are implicit in (analytically contained in) concepts open to a certain sort of elucidation -- then the argument for actually believing in the objects falls apart. Once again, we gain as much purchase on the concept by aligning it with a condition on assumed objects as would be gained by treating the objects as real.
VIII Platonism and primitive ideology
It's an unofficial axiom of metaphysics that we are everywhere faced with "ideology/ontology" tradeoffs. You know the kind of tradeoff I mean: in the work of Lewis and others, primitive metaphysical modality trades off against possible worlds; in the work of Field, primitive logical modality trades off against mathematical objects; in the work of Chisholm, primitive adverbial modification trades off against sense data; in the work of Prior, primitive non-nominal quantifiers trade off against intensional objects like properties and propositions.
How to carry out these tradeoffs is somewhat a matter a taste; some want to minimize semantic primitives at the expense of a bigger than expected ontology, some the reverse. The one seemingly "hard" constraint that has emerged in the area is Davidson's learnability requirement:
When we can regard the meaning of each sentence as a function of a finite number of features of the sentence, we have an insight not only into what there is to be learned [in learning a language]; we also understand how an infinite aptitude can be encompassed by finite accomplishments. For suppose that a language lacks this feature; then matter how many sentences a would-be speaker learns to produce and understand, there will gbe others whose meanings are not given by the rules already mastered. It is natural to say that such a language is unlearnable....we may state the condition under discussion by saying: a learnable language has a finite number of semantical primitives ("Theories of Meaning and Learnable Languages," ITI, 8-9).
Davidson objects again and again to candidate semantic theories that they violate this requirement. He takes on Tarksi and Quine on quotation marks; Scheffler on indirect discourse; Quine on belief attributions; Church on the logic of sense and denotation. Later work extends the argument to theories of adverbial modification and of measurement-predicates like "is 25 degrees Celsius."
The relevance of this to the ontology/ideology issue is that oftentimes the only apparent way of keeping the number of semantic primitives down is to postulate a certain kind of object: Davidson's showcase example, which he wants to make the basis of a new "method of truth in metaphysics," is the postulation of events in service of a tractable semantics for adverbs:
it takes an ontology to make [the device] work: an ontology including people for 'Someone fell down and broke his crown', an ontology of events...for 'Jones nicked his cheek in the bathroom on Saturday.' It is mildly ironic that in recent philosophy it has become a popular manoeuver to try to avoid ontological problems by treating certain phrases as adverbial. One such suggestion is that we can abjure sense-data if we render a sentence like 'The mountain appears blue to Smith' as 'The mountain appears bluely to Smith'. Another..is that we can do without an ontology of intensional objects by thinking of sentences about propositional attitudes as essentially adverbial: 'Galileo said that the earth moves would then come out, 'Galileo spoke in-a-that-the-earth-moves-fashion'. There is little chance, I think, that such adverbial clauses can be given a systematic semantical analysis without ontological entanglements ("The Method of Truth in Metaphysics," ITI, 212-3).
The idea is that if speakers' competence with adverbs is thought of as grounded (potentially anyway) in a mechanism that derives 'S VERBED Gly' from a deep structure along the lines of 'there was a VERBing with agent S which was G,' then there will be no need to learn separate inference rules for each action-verb VERB and adverb G. Both turn into predicates at the level of deep structure and so all logical connections now flow from the finitely representable rules of first-order logic.
The only thing that bothers me about this, construed as a metaphysical argument, is that nowhere in Davidson's explanation of competence is use made of the fact that the events are actually there. At most the conclusion is that we, or pertinent sub-personal systems, are set up to suppose that there are events. Couldn't the supposition be just that: a supposition? Maybe "the adverb mechanism" derives 'S VERBed Gly' not from
(i) 'there was a VERBing with agent S which was G', but
(ii) 'doubts about events aside, there was a VERBing which etc.'
Or maybe it derives 'S VERBed Gly' from (i), but a token of (i) inscribed not in the speaker's "belief box" but her "suppose box." At any rate it is very hard to see how the existence-out-there of real VERBings could lend any real help to the speaker trying to acquire a language; whatever it is that events are supposed to contribute to the language-acquisition task would seem to be equally contributed by merely supposed events.
This is not of course to say that there are no events -- just that one needs a better reason to believe in them than the help they provide with the project of learning a language.
IX Platonism as a prop for realism
One more try: why would anyone want (V), or any other bridge principle, to be literally true, so that the platonic objects it quantifies over were really there?
One can think of this as a query about the relations between ontology, the study of what is, and alethiology, the study of what is the case. A lot of people find it plausible and desirable that what is the case should be controlled as far as possible by what is, and what it is like -- that, in David Lewis's phrase, truth should supervene on being. This is a view that Lewis himself accepts, in the following form: truth is supervenient on what things there are and which perfectly natural properties they instantiate.[14] Since the properties things instantiate are themselves in a broad sense "things," the view is really that truth is supervenient on what things there are and their interactions, e.g., which instantiate which.
Although Lewis maintains this about truth quite generally, it is more common to find it maintained of truth in a specific area of discourse; the usual claim in other words is that truth supervenes on being not globally but only locally.
For instance, it is very often said that what is wrong, or at least different, about moral or aesthetic discourse is that there are no moral/aesthetic properties out there to settle the truth-value of evaluative utterances. And more generally it is common to hear antirealism about F-discourse identified with the thesis that there is no such property as Fness.[15]
But this linking of antirealism about F-discourse with the lack of an associated property is only one symptom of a broader tendency of thought. When truth in an area of discourse is controlled by the existence and behavior of objects, that is felt to boost the discourse's credentials as fact-stating or objective. The more truth can be pinned to the way a bunch of objects comport themselves, the more objective the discourse appears.
"Objective" in what sense? A tradition launched by Dummett says that a discourse is objective if, where S is a statement of the relevant kind, nothing more is needed to settle S's truth value than for its meaning to be made sufficiently clear and precise. IN PARTICULAR: it doesn't matter whether speakers of the language do or would accept that S. Leaving aside the case where the discourse is about our opinions, and leaving aside the role our opinions may play in fixing meaning, the line between truth and falsity in the area is entirely independent of what we think.
The pattern here is a familiar one. Talk about possibility feels more objective if its truth-value is controlled by which possible worlds exist. Talk about what happened yesterday, or what will happen tomorrow, feels more objective if its truth-value is controlled by a still somehow lingering past, or a future out there lying in wait for us.[16] And to return to our original example, talk about validity feels more objective if its truth-value is controlled by the existence or not of countermodels.
Why should objects appear to contribute to objectivity in this way? A little more grandiosely, why should realism -- which holds that a given area of discourse is objective -- seem to be bolstered by platonism -- which points to a special ensemble of objects as determining the distribution of truth values?
Realism says that once you get S's meaning sufficiently clear, its truth value is settled. The question is, settled by what? As long as this question is left hanging, there's room for the anti-realist supicion that we who employ S are exercising an unwholesome influence.
How is the question to be closed? Well, we've got to point to another part of reality that monopolizes the influence on truth-value, leaving no way that we by our attitudinalizing about S could be playing a role.
This is where platonism comes in. The existence of objects, especially external objects, is the paradigm of an issue that's out of our hands. Either worlds with flying pigs are there, or they're not. Either tomorrow's sea battle awaits us, or it doesn't. Either the countermodels exist, or they don't.
X A dilemma
So -- there is this strategy, or tendency of thought, or whatever you want to call it, that links realism in an area of discourse to platonism: belief in a special range of objects whose existence and behavior settles the question of truth. And this strategy in turn helps to explain why people want to be platonists. For certainly one large attraction of platonism -- of the idea that truth depends in a certain area of discourae on being -- is the way it bolsters or appears to bolster the realistic credentials of that area of discourse.
What are we to make of the platonizing strategy? I guess the main thing I want to say is that I find it suspicious. The added confidence that the objects are supposed to give us about the objectivity of the discourse strikes me as unearned, or unneeded, or both. To see why, go back to the example of (V) and (V*). It was seen above that the right hand side of (V), for instance,
(a) this argument has a countermodel
is typically used as though it meant:
(a*) assuming models, this argument has a countermodel .
Clearly (a)'s truth value so understood is independent of the truth value of (b) there are models. But it's just here that the ontologist is going to protest:
You may be right that the truth value of particular claims of form (a) is independent of (b) there are models. What you need (b) for is the objectivity of the form of speech of which (a) and (a*) are examples. If there really are models, then there's an objective fact of the matter about which arguments have countermodels. Take the models away, and all you've got left is the human practice of developing and swapping around model-descriptions. And this practice, not to say it isn't highly disciplined, doesn't provide as objective a basis for validity-talk as a bona fide mathematical space of models would.
I can't say this is without appeal; the models do feel like they provide us with assurances of objectivity. And yet how exactly are the assurances supposed to work? The worry can be put in the form of a dilemma. In logic we speak of "the space of models," the space that allegedly functions via (V) to make discourse about validity especially objective. Do we have a determinate grasp of this space or not? By a determinate grasp, I mean
a grasp sufficient to determine a definite truth value for each instance of "assuming models, there is a countermodel to argument A."
Does our grasp go fatally blurry, for instance, when it comes to models with very large finite cardinalities? Or is it sufficiently precise as to settle the existence of countermodels in every case?
Suppose the latter; we have a determinate grasp in the specified sense. Almost by definition, that by itself ensures that there's a determinate fact of the matter about which arguments have-countermodels-assuming-the-space-of-models.[17] So the models are unneeded; you've got your determinate truth-values without them.
Suppose next that we lack a determinate conception of the space of models; our grasp fails to determine an appropriate truth value for each instance of "assuming the space of models, there is a countermodel to argument A." How is it that we nevertheless manage to pick out the right class of mathematical objects as models?
The answer has got to be that the world meets us half way. The intended objects somehow jump out and announce themselves, saying: over here, we're the ones you must have had in mind. A particularly attractive form of this is as follows: look, we're the only remotely plausible candidates for the job that even exist. This amounts to saying that we understand the space of models as whatever out there best corresponds to our otherwise indeterminate intentions.
But such a response reintroduces the hostage-to-fortune problem. An argument's validity-status would seem to be a conceptually necessary fact about it. Surely we don't want the validity of arguments to be held hostage to a brute logical contingency like what model-like entities happen to exist! (This feeling of not wanting brute ontological facts to influence validity is part of what lies behind John Etchemendy's rejection of Tarski's principle in The Concept of Logical Consequence.)
So Tarski's principle (considered now as objectivity-bolstering) is faced with a dilemma. If we are clear enough about what we mean by it, then the principle isn't needed for objectivity; you can use (V*). And if we aren't clear what we mean, then it isn't going to help. It isn't even going to be tolerable because an argument's status as valid is going to blow with the ontological winds in a way that no one could possibly want.
XI Crime of the century?
It begins to look like the objectivity argument does not really work. The objects would only be needed if they "stiffened the discourse's spine" -- if they had consequences for truth-values over and above anything determined already by our conception of the objects. But by that fact alone, we wouldn't trust them to deliver the right results.
The reason this matters is that as far as I can see, the objectivity argument is the only one that argues for a truth-link with actual objects. The other principal motives for accepting platonic objects are served just as well by pretended or assumed ones.
Which suggests a wild idea. Could it be that sets, functions, properties, worlds, and the like, are one and all put-up jobs, meaning, only assumed to exist? Call this the say -hypothesis, because what it essentially says is that most talk of platonic objects should be understood as following on an unspoken "say there are models (or whatever)" prefix.
How to evaluate the say-hypothesis? Bertrand Russell once said that postulation of objects has all the advantages of theft over honest toil. This might seem to apply to the say hypothesis as well. The suggestion in a way is that an enormous intellectual crime has been committed; an entire species of much-beloved and frequently deferred-to objects has been stolen away, leaving behind only persistent appearances.
Suppose we discuss the alleged theft of the platonic objects the way we would any other alleged crime. Means, motive, opportunity -- are all these elements present?
The question of means is: how would a job like this be pulled off, where objects appear to be in play but really aren't? The question of motive is: why would anyone want to fabricate these objects in the first place? The question of opportunity is: how could a job this big be pulled off without anyone noticing?
XII Means
How might it happen that, of the things that regularly crop up in people's apparently descriptive utterances, not all really exist, or are even believed to exist by the speaker?
Before we can get anywhere with this question, we need to acknowledge the feelings of dishonesty it arouses in us. A certain effortless indignation about theorists who "refuse to own up to the commitments of their own speech" has long been the rule in philosophy. The attitude goes back at least to Word & Object, where Quine misses no opportunity to deplore the "philosophical double talk, which would repudiate an ontology while simultaneously enjoying its benefits" (242).
But rhetoric aside, the phenomenon of people putting statements forward that don't, as literally understood, convey their true meanings is extraordinarily familiar and common. The usual word for it is "indirect speech." I utter the words "would you mind getting off my foot?" not to express curiosity about your preferences, but to make a request. I say "this might be a good place to spend the night" not to offer a conjecture but make a suggestion. I say "that's not such a great idea" not to call your idea less-than-great -- leaving it open, as it were, that it might be very good -- but to call your idea bad.
This last example, of calling an idea not so great meaning that it is quite bad, reminds us that one kind of indirect speech is figurative speech. The figure in this case is understatement, but the point could equally have been made with, say, hyperbole ("they are inseparable"), metonymy ("the White House is angry over allegations that..."), or metaphor ("I lost my head"). Not one of the sentences mentioned has a true literal content: the first because it exaggerates, the second because it conflates, the third or reasons still to be explored. But it would be insane to associate the speaker with these failings, because the sentences' literal content (if any) is not what the speaker is putting forward.
The most important example for us is metaphor; but what exactly is that? The most promising account I have seen is Ken Walton's in terms of prop oriented make-believe:
Where in Italy is the town of Crotone? I ask. You explain that it is on the arch of the Italian boot. 'See that thundercloud over there -- the big, angry face near the horizon,' you say; 'it is headed this way.'...We speak of the saddle of a mountain and the shoulder of a highway....All of these cases are linked to make-believe. We think of Italy and the thundercloud as something like pictures. Italy ... depicts a boot. The cloud is a prop which makes it fictional that there is an angry face...The saddle of a mountain is, fictionally, a horse's saddle. But ... it is not for the sake of games of make-believe that we regard these things as props...[The make-believe] is useful for articulating, remembering, and communicating facts about the props -- about the geography of Italy, or the identity of the storm cloud...or mountain topography. It is by thinking of Italy or the thundercloud...as potential if not actual props that I understand where Crotone is, which cloud is the one being talked about.[18]
A metaphor on this view is an utterance that represents its objects as being like so: the way that they would need to be to make the utterance the right kind of thing to be taken as true - to be said-true -- in a game that it itself suggests. Sayability here is a function of two factors: the game's rules, and the way of the world. The point of uttering the metaphor is to say that the world has held up its end of the bargain.
Normally when people talk about metaphor, the examples that come to mind are of metaphorical descriptions of everyday objects; thus a hat is divine, or a person is green with envy, or beside herself with excitement.. Predicative expressions, though, are far from the only ones we use metaphorically; there is hardly a word in the language, be it an adverb, preposition, conjunction, or what have you, that is devoid of metaphorical potential. The case that interests us, of course, is referring phrases : names, definite descriptions, and quantifiers. An appendix to the Metaphors Dictionary lists 450 examples of what it calls "common metaphors." Approximately one-half contain referential elements. Some examples drawn just from the beginning of the list:
he fell into an abyss of despair, the apple doesn't fall far from the tree, he is tied to her apron strings , she has an axe to grind, let's put that on the back burner, those figures are in the ballpark, you're beating a dead horse, he's bit off more than he can chew, don't hide your lamp under a bushel , let's go by the book, don't blow a fuse, I have a bone to pick with you, I've burned my bridges, I hate to burst your bubble, you hit the bullseye, I have butterflies in my stomach, I'm going to lay my cards on the table, you're building castles in the air, we will be under a cloud until we settle this thing, he claimed his pound of flesh, she blew her cool, he threw me a curve, their work is on the cutting edge
Some additional examples of my own; with some of them you have to rub your eyes and blink twice before its non-literal character comes through:
they put a lot of hurdles in your path, there's a lot that could be said about that, there's no precedent for that, something tells me you're right, there are some things better left unsaid, there is something I forgot to tell you, viz. how to operate the lock, nothing gets my goat as much as chewing gum in class, a lot you can do for me, judge then of my surprise, let's roll out the red carpet, the last thing I want is to ..., they have been rising in my esteem, I took her into my confidence, I'll take my chances, there's a trace of sadness in your eyes, a growing number of these leaks can be traced to Starr's office, she's got a lot of smarts , let's pull out all the stops; let's proceed along the lines suggested above
Now, the last thing I want to do with these examples is to start a bidding war over who can best accommodate our classificatory intuitions. The one unbreakable rule in the world of metaphor is that there is little to no consensus on how big that world is: on what should be counted a metaphor and what should not. What I do want to suggest is that the same semantical mechanisms that underlie paradigmatic metaphors like "your perfume is divine" seem also to be at work with phrases that for whatever reason -- too familiar, insufficiently picturesque, too boring -- strike us as hardly figurative at all. If that is right, then it does little harm I think to stipulate that any phrases which turn an unserious "say it's like this" to descriptive advantage are to be seen as just as much metaphorical as the old campaigners.
This brings me to the main claim of the section. The means by which platonic objects are simulated is existential metaphor -- that is, metaphor making play with a special sort of object to which the speaker is not committed (not by the metaphorical utterance, anyway) and to which she adverts only for the light it sheds on other matters. Rather as "smarts" are conjured up as metaphorical carriers of intelligence, "numbers" are conjured up as metaphorical measures of cardinality. More on this below; first there are the questions of motive and opportunity to deal with.
XIII Motive
What is the motive for simulating platonic objects in this way? The motive is that lots of metaphors, and in particular lots of existential metaphors, are essential . They have no literal paraphrases; and/or, none with equally happy cognitive and motivational effects.
To elaborate a little on the picture so far, a metaphor has in addition to its literal content -- given by the conditions under which it is true and to that extent belief-worthy -- a metaphorical content given by the conditions under which it is "sayable" in the relevant game. If we help ourselves in a purely heuristic spirit[19] to the device of possible worlds, we can put it like so:
S's literal/metaphorical content = the set of worlds making S true/sayable.
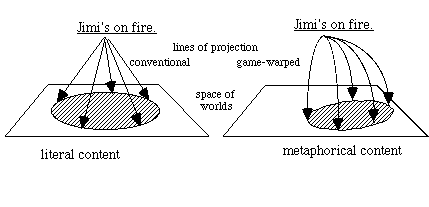
The role of say-games on this approach is to warp the usual lines of semantic projection, so as to reshape the region a sentence defines in logical space:[20]

The straight lines on the left are projected by the ordinary, conventional meaning of "Jimi's on fire"; they pick out the worlds which make "Jimi's on fire" true. The bent lines on the right show what happens when worlds are selected according to whether they make the very same sentence, meaning the very same thing, sayable in the relevant game.
The question of motive can be put like this: granted these metaphorical contents -- these ensembles of worlds picked out by their shared property of legitimating an attitude of acceptance-within-the-game -- what is the reason for accessing them metaphorically?
One obvious reason would be lack of an alternative: the language might have no more to offer in the way of a unifying principle for the worlds in a given content than that they are the ones making the relevant sentence sayable. It seems at least an open question, for example, whether the clouds we call angry are the ones that are literally F, for any F other than "such that it would be natural and proper to regard them as angry if one were going to attribute emotions to clouds." Nor does a literal criterion immediately suggest itself for the pieces of computer code called viruses, the markings on a page called tangled or loopy, the glances called piercing, or the topographical features called basins, funnels, and brows.
The topic being ontology, though, let's try to illustrate with an existential metaphor. An example much beloved of philosophers is the average so-and-so.[21] When someone says that
(S) The average star has 2.4 planets,
she is not entirely serious; she is making as if to describe an (extraordinary) entity called "the average star" as a way of really talking about what the (ordinary) stars are like on average. True, this particular metaphor can be paraphrased away, as follows:
(T) The number of planets divided by the number of stars is 2.4,
But the numbers in T are from an intuitive perspective just as remote from the cosmologist's intended subject matter as the average star in S. And this ought to make us, or the more nominalistic among us, suspicious. Wasn't it Quine who stressed the possibility of unacknowledged myth-making in even the most familiar constructions? The nominalist therefore proposes that T is metaphorical too; it provides us with access to a content more literally expressed by
(U) There are 12 planets and 5 stars or 24 planets and 10 stars or...[22]
And now here is the rub. The rules of English do not allow infinitely long sentences; so the most literal route of access in English to the desired content is T, and T according to the nominalist is a metaphor. It is only by making as if to countenance numbers that one can give expression in English to a fact having nothing to do with numbers, a fact about stars and planets and how they are numerically proportioned.[23]
Whether you buy the example or not, it gives a good indication of what it would be like for a metaphor to be "representationally essential," that is, unparaphrasable at the level of content; we begin to see how the description a speaker wants to offer of his intended objects might be inexpressible until unintended objects are dragged in as representational aids.
Hooking us up to the right propositional contents, however, is only one of the services that metaphor has to offer. There is also the fact that a metaphor (with any degree of life at all) "makes us see one thing as another"; it "organizes our view" of its subject matter; it lends a special "perspective" and makes for "framing-effects."[24] Here is Dick Moran:
To call someone a tail-wagging lapdog of privilege is not simply to make an assertion of his enthusiastic submissiveness. Even a pat metaphor deserves better than this...the comprehension of the metaphor involves seeing this person as a lapdog, and...experiencing his dogginess.[25]
The point here is not especially about seeing-as, though, and it is not only conventionally "picturesque" metaphors that pack the intended sort of cognitive punch. This is clear already from scientific metaphors like feedback loop, underground economy, and unit of selection. But let me illustrate with a continuation of the example started above.
Suppose that I am wrong and "the average star has 2.4 planets" is representationally accidental; the infinite disjunction "there are five stars and twelve planets etc." turns out to be perfect English. The formulation in terms of the average star is still on the whole hugely to be preferred -- for its easier visualizability, yes, but also its greater suggestiveness ("that makes me wonder how many moons the average planet has"), the way it lends itself to comparison with other data ("the average planet has six times as many moons as the average star has planets"), and so on.[26]
A second example has to do with the program of "first-orderizing" entailment relations.[27] Davidson in "The Logical Form of Action Sentences" says that a key reason for rendering "Jones VERBed Gly" as "there was a VERBing done by Jones which was G" is that the argument from "Jones VERBed Gly" to "Jones VERBed" now becomes quantificationally valid. Of course, similar claims are often made on behalf of the possible worlds account of modality; unless you want the inference from "possibly S" to "possibly S-or-T" to be primitive and unanalyzable, you'd better understand "possibly S" as "there is a world making S true." Any number of authors have made this sort of plea on behalf on propositions; how without quantifying over them can you hope to first-orderize the inference from "I believe whatever the pope believes" and "the pope believes abortion is wrong" to "I believe abortion is wrong"?
The claim these authors make is not that the relevant contents are inexpressible without quantifying over events, or worlds, or what have you; that would be untrue, since the contents can clearly be expressed via sentences like "she did it skilfully" and "possibly BLAH." The claim is that the logical relations among these contents become much more tractable if we represent them quantificationally. So represented the contents wear their logical potential on their sleeve, at least from the perspective of a first-order-savvy audience like the community of professional philosophers.[28]
Back to the main thread: Along with its representational content, we need to consider a metaphor's "presentational force." Just as it can make all the difference in the world whether I grasp a proposition under the heading "my pants are on fire," grasping it as the retroimage of "Crotone is in the arch of the boot" or "the average star has 2.4 planets" or "there is a world with blue swans" can be psychologically important too. To think of Crotone's location as the place it would need to be to put it in the arch of Italy imagined as a boot, or of the stars and planets as proportioned the way they would need to be for the average star to come out with 2.4 planets, is to be affected in ways going well beyond the proposition expressed. That some of these ways are cognitively advantageous gives us a second reason for accessing contents metaphorically.
XIV Opportunity:
Now for the question of opportunity. How are these metaphors slipped in without anyone's noticing?
The first thing that has to be said is that figurative elements in our speech are very often unconscious, and resistant to being brought to consciousness. To hear "that wasn't very smart" (understatement) or "a fine friend she turned out to be" (irony) or "spring is just around the corner" (metaphor) as meaning what they literally say takes a surprising amount of effort. The best comparison I can think of is with the effort famously involved in making out the color of the paint in the center of an impressionist painting.
As the painting analogy suggests, a too-vivid appreciation of literal meaning can interfere with the attempted figure. Wittgenstein tells of an art-lover leaning up to the bloodshot eyes in a Rembrandt painting and saying "that's the color I want for my bathroom curtains." Such a person is not -- not at that moment, anyway -- in tune with the painting's representational ambitions. Just so, overzealous attention to what a "gutsy idea" would be like, or what it would really be to "keep your eyes peeled," or "pour your heart out" to your beloved, prevents any real appreciation of the intended message.
If you're with me this far, consider now statements like "there's something Jones is that Smith isn't: happy" or "another way to get there is via Tegucigalpa"? Taken at face value, these sentences do indeed commit themselves to entities called "happy" and "via Tegucigalpa." But overmuch attention to the fact is likelier to distract from the speaker's intended meaning than to illuminate it; what on earth could via Tegucigalpa be? Likewise someone who says that "the number of Democrats is on the rise" wants the focus to be on the Democrats, not "their number," whatever that might be. Their number is called in just to provide a measure of the Democrats' changing cardinality; it's expected to perform that service in the most inconspicuous way and then hustle itself off the stage before people start asking the inevitable awkward questions, e.g., which number is it? 50 million? is 50 million really on the rise?
A second reason for the unobtrusiveness of existential metaphors takes longer to explain. Earlier we distinguished two qualities for which a metaphor might be valued: its representational content, and its presentational force. But that can't be the whole story. For we are still conceiving of the speaker as someone with a definite message to get across, and the insistence on a message settled in advance is apt to seem heavy-handed. "The central error about metaphor," says Davidson, is to suppose that
associated with [each] metaphor is a cognitive content that its author wishes to convey and that the interpreter must grasp if he is to get the message. This theory is false...It should make us suspect the theory that it is so hard to decide, even in the case of the simplest metaphors, exactly what the content is supposed to be.[29]
Whether or not all metaphors are like this, one can certainly agree that a lot are: perhaps because, as Davidson says, their "interpretation reflects as much on the interpreter as on the originator"[30]; perhaps because their interpretation reflects ongoing real-world developments that neither party feels in a position to prejudge. Either way, one can easily bring this third, opportunistic, grade of metaphorical involvement under the same conceptual umbrella as the other two:
Someone who utters S in a metaphorical vein is recommending the project of (i) looking for games in which S is a promising move, and (ii) accepting the propositions that are S's inverse images in those games under the modes of presentation that they provide.
The overriding imperative here is to make the most of it;[31] construe a metaphorical utterance in terms of the game or games that retromap it onto the most plausible and instructive contents in the most satisfying ways.
Now, should it happen that the speaker has definite ideas about the best game to be playing with S, then I myself see no objection to saying that she intended to convey a certain metaphorical message -- the first grade of metaphorical involvement -- perhaps under a certain metaphorical mode of presentation -- the second grade.[32] So it is, often enough, with "I lost my cool" or "that dog won't hunt."
The reason for the third grade of metaphorical involvement is that one can imagine various other cases, in which the speaker's sense of the potential metaphorical truthfulness of a form of words outruns her sense of the particular truth(s) being expressed. Consider the case of the pregnant metaphor, which yields up indefinite numbers of contents on continued interrogation;[33] the prophetic metaphor, which expresses a single content whose identity, however, takes time to emerge;[34] and, importantly for us, the patient metaphor, which hovers indefinitely above competing interpretations, as though waiting to be told where its advantage really lies.
The interesting thing is that is that it is this third grade of metaphorical involvement, supposedly at the furthest remove from the literal, that can be hardest to tell apart the literal. The reason is that one of the contents that my utterance may be up for, when I launch S into the world in the opportunistic spirit described above, is its literal content. I want to be understood as meaning what I literally say if my statement is literally true -- count me a player of the "null game," if you like -- and meaning whatever my statement projects onto via the right sort of "non-null" game if my statement is literally false. It is thus indeterminate from my point of view whether I am advancing S's literal content or not.[35]
Isn't this in fact our common condition? When people say that there are more ways of getting to Houston than to Gatlinburg, that the number of As = the number of Bs, that they have tingles in their legs, or that Nixon had a stunted superego, they are far more certain that S is getting at something right than that the thing it is getting at is the proposition that S, as some literalist might construe it. If numbers exist, then yes, we are content to regard ourselves as having spoken literally. If not, then the claim was that the As and Bs are equinumerous.[36] If Freud was right, then yes, Nixon had a superego and it really was stunted. If not, then the claim was (more or les) that Nixon had trouble telling when a proposed course of action was morally wrong or not.
All right, but what does this have to do with the inconspicuousness of platonic metaphors? The fact that I could for all anyone knows -- for all that I myself know -- be speaking literally goes some way towards explaining why these metaphors do not attract attention to themselves. If a literal interpretation is always and forever in the offing, and if no real harm can come of adopting it for argument's sake, then the fact that a metaphorical interpretation is similarly always and forever possible is liable to escape our notice.
XV ...Lost?
Of all the reasons people give for thinking that platonic metaphors couldn't have slipped in unnoticed, the most common is this. I speak metaphorically only if I speak in a way that is guided by, but somehow at odds with, my notion of what would be involved in a literal deployment of the same sentence. The literal meaning is not mine, but I have to be exploiting or making play with it - I have at any rate to set myself up in opposition to it -- if I am to count as a metaphorist. [37] This immediately suggests a negative test. Metaphors are, says Fowler, "offered and accepted with a consciousness of their nature as substitutes." So in the absence of any such consciousness -- in the absence of a literal meaning the speaker can point to as exploited where it might instead have been expressed -- there is no metaphor. Call this the "felt distance" test for metaphorical utterance.
Now we're ready for the objection. If the felt distance test is right, then my claim that, say, "10 is the number of my toes" cannot possibly be metaphorical. For look at what the test tells me. It says that for the claim to be metaphorical I should experience myself as guided by meanings of "number" or "10" that I am at the same time somehow disrespecting or making play with. But I am not aware of being guided by any such disrespected meanings. I do not even have a conception of what those meanings could be; it hardly seems possible to use the words "number" and "10" more literally than I already do.
I have two responses to this, one which accepts the felt distance test for the sake of argument, one which finds the test unreliable. The first response goes as follows. When you assume that the words being used metaphorically in "10 is the number of my toes" are "number" and "10," you are barking up the wrong tree. By a "number" we mean something like this: entity of a kind that is suited by its intrinsic nature to providing a measure of cardinality -- the number of BLAHs, for instance, is suited by nature to serving as a mark or measure of how many BLAHs there are -- and that has not a whole lot more to its intrinsic nature than that. The literal meaning of "10" is: number that provides a measure, cardinality-wise, of the BLAHs iff there are ten BLAHs. These are exactly the meanings with which "number" and "10" are used in "10 is the number of my toes." So you are wrong to think that the metaphoricality of "10 is the number of my toes" hinges on a metaphorical usage of those two words.
Now though the objector wants to know which words are being used metaphorically.[38] Well, for all anyone really knows, numbers in the indicated sense don't exist; nothing exists whose intrinsic nature is exhausted by the considerations mentioned. Someone opining that "10 is the number of my toes" is not really concerned about that, however; they are taking the numbers for granted in order to call attention to their real subject matter, viz. how many toes they have. This suggests that it is the definite article "the," or rather the existential quantifier it implicitly contains, that is being used metaphorically. The reason this matters is that the existential quantifier passes the felt- distance test. When I assume for metaphorical purposes that numbers exist, I am guided by, but at the same time (running the risk of) disrespecting, the literal meaning of "exists"; for using "exists" literally, numbers may well not exist, in which case "10 is the number of my toes," ie., "there is a number which numbers my toes and which is identical to all numberers of my toes and which is 10," is literally false.
Secondly, though, the felt-distance test is wrong. It is true is that if I am to use a sentence S metaphorically, there had better be conditions under which S is pretense-worthy, and conditions under which it is not pretense-worthy. But as we know from the example of fiction, this does not require that S possesses a literal meaning, as opposed to fictionally possessing one in the relevant make-believe game. Flann O'Brien in The Third Policeman tells of a substance called "gravid liquid," the tiniest drop of which weighs many tons, and whose subtle dissemination through the parts of material objects is all that prevents them from floating away. When I pretend in discussions of that book that gravid liquid cannot be held in a test tube, I am guided by my idea of what "gravid" is supposed in the game to mean; I have no concern at all about what it means in English, and for all I know it is not even an English word.[39] An example more to the present point is this. "Smart" in my dictionary is an adjective, not a noun. How is it that we can say "she has a lot of smarts" and be understood? Well, it is part of the relevant make-believe game that there are these entities called "smarts" that are somehow the carriers of intelligence; the more of them you have, the smarter you are. The make-believe meaning of "smart" as a noun is of course informed by its literal meaning as an adjective. Who is to say it is not the same with "ten"; the meaning it is pretended to have qua noun is informed by its literal meaning qua adjective.
I don't know which of these two responses to prefer; but let me call attention to a point of agreement between them. A metaphor for us is a supposition adverted to not because it is true but because it marks a place where truths are thought to lie. It is compatible with this that certain words might be used more often in a metaphorical vein rather than a literal one; it is compatible with it even that certain words should always be used metaphorically because they lack literal meaning. This points to a third reason why some metaphors do not call attention to themselves. Standard usage is easily confused with literal usage -- all the more so when an expressionhas no literal use with which the standard use can be constrasted. Since platonic metaphors are nothing if not standard, it would be only natural if they shared in this larger inconspicuousness. One doesn't notice that talk of tingles is maybe-metaphorical until one reflects that "I have tingles in my legs" would not be withdrawn even in the proven absence of tingles. Likewise, the way that platonic metaphors reveal themselves is through our (otherwise very peculiar! ) insouciance about the existence or not of their apparent objects.
XVI Suggestive similarities
The bulk of this paper has been an argument that it is less absurd than may initially seem that references to platonic objects in everyday speech are not to be taken literally. If someone suspects that the objects are not really there -- that, to revert to the crime analogy, they have been "stolen away" -- it seems like means, motive, and opportunity for the alleged caper are not all that hard to make out.
Of course, it is one thing to argue that a metaphorical construal is not out of the question, another to provide evidence that such a construal would in fact be correct. That's what I want to do now, by listing a series of similarities between platonic objects, on the one hand, and creatures of metaphorical make-believe, on the other, that strike me as being at the very least suggestive. Some of these similarities will just restate in other terms material that was presented earlier, some of them will be new. I want to stress that none of these similarities is anything like decisive, and that not all the features mentioned are common to all POs -- platonic objects -- or to all MBs -- creatures of metaphorical make-believe. But the cumulative effect is I think nothing to sneeze at.
|
PARAPHRASABILITY |
|||
|
MBs are often paraphrasable away with no felt loss of subject matter. "That was her first encounter with the green-eyed monster" goes to "that was her first time feeling jealous." "That really gets my goat goes to "that really irritates me." |
POs are often paraphrasable away with no felt loss of subject matter. "There is a possible world at which S" goes to "it is possible that S." "She did it in some way or other" goes to "she did it somehow." Etc. |
||
|
IMPATIENCE |
|||
|
One is impatient with the meddling literalist who wants us to get worried about the fact that an MB may not exist. "I wasn't supposing there really was a green-eyed monster" |
One is impatient with the meddling ontologist who wants us to get worried about whether a PO, or type of PO, really exists. "Well, say there are models; then this argument has a countermodel." |
||
|
TRANSLUCENCY |
|||
|
About the best one can do with "What if there is no green-eyed monster?" is to hear it as the (bizarre) suggestion that no one is ever really jealous. |
About the best one can do with "what if for every world, there's another more populous one?" is to hear it as the (not so bizarre) suggestion that you can always have one more thing. |
||
|
INSUBSTANTIALITY |
|||
|
Unlike ordinary objects, MBs tend to have not much more to them than what flows from our conception of them. The green-eyed monster has no "hidden substantial nature"; neither do the real-estate bug, the blue meanies, the chip on my shoulder, ... |
Unlike ordinary objects, POs often have not much more to them than what flows from our conception of them. All the really important facts about the numbers follow from (2nd order) Peano's Axioms. Likewise for sets, functions, .... |
||
|
INDETERMINACY |
|||
|
Unlike ordinary objects, MBs can be "indeterminately identical." There is no fact of the matter as to the identity relations between the fuse I blew last week and the one I blew today, or my keister and my wazoo ("I've had it up to the keister/wazoo with this paperwork") . The relevant game(s) leave it undecided what is to count as identical to what. |
Unlike ordinary objects, POs can be "indeterminately identical." There is no fact of the matter as to the identity relations between the pos. integers and the Zermelo numbers, or the worlds and the maximal consistent sets of propositions, or the events and the property-instantiations. It is left (partly) undecided what is to count as identical to what. |
||
|
SILLINESS |
|||
|
MBs invite "silly questions" probing areas the make-believe does not address, e.g., we know how big the average star is, where is it located? you say I have risen in your esteem, by how many inches? do you plan to drop-forge the conscience of your race in the smithy of your soul? |
POs invite questions that seem similarly silly. [40] What are the intrinsic properties of the empty set? Is the event of the water's boiling itself hot? Are universals wholly present in each of their instances? Do relations lead a divided existence, parcelled out among their relata? |
||
|
EXPRESSIVENESS |
|||
|
MBs show a heartening tendency to boost the language's power to express facts about other, more ordinary, entities. "Your typical taxpayer saves an increasing portion of his/her income." |
POs show a strong tendency to boost the language's power to express facts about other, more ordinary, entities. "The boundary of this circle is pi times as long as its diameter." |
||
|
IRRELEVANCE |
|||
|
MBs are called on to "explain" phenomena that would not on reflection suffer by their absence. Even if the "typical taxpayer" had not existed, because the relevant distributions were multimodal, the savings rate would still have increased. |
POs are called on to "explain" phenomena that would not on reflection suffer by their absence. If all the one-one functions were killed off today, there would still be as many left shoes in my closet as right. |
||
|
DISCONNECTEDNESS |
|||
|
MBs have a tendency not to do much other than expressive work. As a result, perhaps, of not really existing, they tend not to push things around. |
POs have a tendency not to do much other than expressive work; numbers et al. are famous for their causal inertness. [41] |
||
|
AVAILABILITY |
|||
|
MBs' lack of naturalistic connections might seem to threaten epistemic access -- until we remember that "their properties" are projected rather than detected. |
POs' lack of naturalistic connections are widely thought to threaten epistemic access - the threat evaporates if "their properties" are projected, not detected. |
||
Of course we should not forget one final piece of evidence for the make-believe nature of platonic objects. This is the fact that a metaphorical interpretation of POs solves our original paradox. (And I'm not aware that it has any serious competition here.) Our reluctance to infer the existence of models from the Tarski biconditionals is just what you'd expect if the inference goes through only on a literal interpretation, and the biconditional is not in the end taken literally.
XVII Concluding unscientistic postscript
If the a priori approach to ontological questions is undermined by doubts about literality, then Quinean indispensability arguments might seem to be the only game left in town. But it seems to me that Quine's ontological program is in a related sort of trouble.[42]
The Quinean says that we should believe in Xs just to the extent that we find it hard to avoid quantifying over them in our scientific theories. That would be fine if the quantifiers were all to be taken literally. But some quantifiers are metaphorical. That would be fine too if the metaphorical quantifiers could be counted on to disappear as theory progressed. But some metaphors are essential and so presumably permanent.
Not even Quine thinks that figurative quantification is ontologically committal; why should I should take ontological advice from a theory whose literal content I do not even believe? A consistent Quinean should therefore want us to ferret out all traces of non-literality in our theories before we turn to them for ontological guidance. To the extent that there is no sensible project of doing that, there is no sensible project of Quinean ontology. All I will say here is that I fear the worst.
Appendix A: Paraphrase
A priori-looking bridge principles of the kind discussed in this paper have frequently appeared in philosophy with their left and right hand sides reversed. That is, instead of
it is possible that B iff there is a B-world,
there are as many Cs as Ds iff the number of Cs = the number of Ds,
x is H iff x has the property of Hness,
we are told that
there is a B-world iff it is possible that B
the number of Cs = the number of Ds iff there are as many Cs as Ds
x has the property of Hness iff x is H.
Written this second way, the biconditionals present themselves as devices for shrugging off the ontological commitments apparently incurred by their left hand sides.[43] Whenever you are tempted to say that the number of Fs is the number of Gs, you should say instead that the Fs are equinumerous with the Gs. And so on. (Or, treat the rewritten biconditionals' left hand sides as possibly misleading shorthands for what is properly expressed in the less ontologically committal terms indicated on the right.)
Now, it should be clear that any platonic object worth its salt cannot be shrugged off quite so easily; see section XII above and the next Appendix.
But even ignoring that, the "paraphrase" gambit presents a real puzzle -- first noted by William Alston in "Ontological Reduction," and much emphasized by Crispin Wright in his book on numbers.[44]
The notion of paraphrase is torn between two incompatible-looking aspirations. On the one hand there's an aspiration to symmetry: paraphrases are supposed to match their originals along some important semantic dimension. On the other hand there's an aspiration to asymmetry: paraphrases are supposed to fix their originals by shedding unwanted ontological commitments.
The difficulty of course is to see how can you have the matching and the fixing together . It is not easy to think of a dimension or aspect of meaning such that sentences can mean the same along that dimension despite the fact that they assert the existence of different things.
Quine's solution in Word & Object is to sacrifice matching to fixing. He says that he expects nothing like synonymy from a paraphrase but just a sentence that "serves any purposes of [the original] that seem worth serving."[45] This is technically unanswerable, but ignores our feeling in many cases that the paraphrase "says the same" as what it paraphrases, or the same as what we were trying to say by its means.
Alston and Wright go the opposite way, sacrificing fixing to matching. Contrary to what we naturally suppose, they say, "there are as many Cs as Ds" carries the same commitment to numbers evident in "the number of Cs = the number of Ds." But then why did the paraphrase seem so ontologically liberating? Was it pure confusion to think that "I have as many left hands as right" was compatible with "there are no abstract objects"?
What we would like, of course, is matching and fixing together. There is a clue as to how this might be arranged in the word "paraphrase" itself. Is it just a coincidence that the word is encountered more often in poetry class than anywhere else? I suggest not, and that the poetry-class notion gives us all we need. The poetry-class notion (crudified, but not in a way that matters) is this:
(#) PS is a paraphrase of S iff PS expresses in literal terms what S metaphorically.
With (#) in mind, let S be "the number of Cs is the number of Ds" and PS be "the Cs are equinumerous with the Ds." Then we get matching in the sense that
the literal content of PS = the metaphorical content of S,
and fixing in the sense that
the literal content of S requires numbers, that of PS does not.
This puts aspects of the nominalist/realist debate in a different light. The nominalist who sees in S a misleading way of putting what is better expressed by PS is quite right: there's a very real danger that S will be taken literally. The realist who sees the reference to numbers in S as more than a notational convenience is right too. Their appearance in S is crucial if we want to preserve inferential links with sentences S' (e.g., "if m = n, then m+n is even") that are not so easily provided with numberless paraphrases.
Appendix B: Three Degrees of Platonic Involvement
I have been emphasizing various kinds of expressive advantage afforded by existential metaphor: representational, presentational, procedural, and so on. The most important is probably the first. To put it as dramatically as I know how, if numbers did not exist, we would have to pretend they did in order to gain access to desired contents. Add to this that pretend numbers are just as good (representationally speaking) as real ones, and the tempting conclusion is that numbers (and other platonic objects) don't exist, and no great loss.
An objection may occur to you at this point. Platonic objects were defined as whatnots that turn up on the right hand sides of a priori-looking bridge biconditionals whose left hand sides made no mention of any such whatnots. The objection is: If the two sides are really equivalent, then how can the access platonic objects buy us to the right hand sides possibly boost the language's representational powers? Anything you might try to express with the right side -- say, with a condition on models -- is by definition also expressible with left -side language. So, how can the models be helping?
The answer to this is that it is quite right as far as it goes; the conditions figuring on the right hand sides of bridge biconditionals do not express contents that would be otherwise inaccessible. But that's OK, because that's not where the expressive novelty comes in. Once you've got the platonic objects on board, you can use them to formulate new conditions. And these new conditions might very well take you into uncharted representational territory.
First example: models are not valued because of the access they buy you to the content of "every model of A's premises is a model of its conclusion." That content was already available courtesy of "A's premises entail its conclusion." But consider the relation, already mentioned, that obtains between A's premises and its conclusion when all minimal models of the premises are models of the conclusion.[46] Relations like have been of some importance in work on the frame problem and default reasoning, and it was the the use of model-theoretic methods that made them available.
Second example: A lot of the modal claims we want to make are expressible in ordinary English using modal adverbs like "necessarily" and "possibly," without any explicit mention being made of worlds. But Davies and Humberstone have used the apparatus of possible worlds to introduce a locution "fixedly" which (one might think) was not expressible in ordinary English.[47]
Why not? Well, the "fixedly" operator falls into the class of what Kaplan calls "monsters begat by elegance" -- it is an operator on character rather than content -- and the existence of such an item in English would violate the principle that, roughly, indexicals always get widest scope.[48] One can give a hint of what "fixedly" means by saying that it's the modal counterpart to "always" interpreted so that "it's always now" comes out true, or "wherever" interpreted so that "wherever I go, here I am."[49] But the indicated variants of "always" and "wherever" are themselves in violation of Kaplan's principle and so not properly English if he is right.[50]
The moral is that we need to distinguish different contexts in which platonic objects can turn up. One place is on the right hand side of biconditionals giving the truth-conditions of "already understood" English sentences -- and we can throw in here contexts where their appearance is licensed by such a biconditional.
The advantages that platonic objects confer in these -- call them analytic -- contexts are presentational rather than representational. A prominent example is the so-called "first-orderization" of entailment relations already discussed. Against the background of appropriate bridge principles, that B entails "possibly, B" can be read off the fact "there is a B-world" follows in first order logic from "the actual world is a B-world." Similarly, that "there are as many Cs as Ds and as many Ds as Es" entails "there are as many Cs as Es" emerges from the first-order truth that if n=m and m=p then n=p.[51]
As we have seen, platonic objects can also turn up in contexts where they are representationally essential: contexts where they faciliate the expression of contents that are not the literal contents of any English sentence. Once you've got these contents in hand you can introduce sentences that will express them literally:
"A is circumscriptively valid" is literally true iff -- using the metaphor of models, now -- minimal models of A's premises are models of its conclusion.[52]
"fixedly B" is literally true iff -- using the metaphor of worlds, now -- take any world w you like, if w is actual, then B.
"there are r times as many Cs as Ds" is literally true iff -- using the metaphor of numbers -- r times the number of Ds = the number of Cs
Since platonic objects in this sort of use buy us access to new contents -- the notions of circumscriptive validity and so on first make their way into the language via a condition on platonic objects -- contexts of the second type will be called creative.
A third context for platonic objects is in sentences with respect to which they are, well, not platonic: Recall that "platonic" is a relational notion: Xs are platonic with respect to a discourse R iff they turn up in truth-conditions of R-sentences that are not intuitively about Xs. But there are plenty of sentences around that are intuitively about numbers, sets, models, and the like, e.g., "there are prime numbers over 100," "there are infinitely many sets," and "possible worlds are concrete rather than abstract." Since numbers and the rest do not figure here as part of a representational apparatus directed at other things, contexts of this third type will be called autonomous.
Autonomous contexts might be seen as making the strongest case for belief in POs, because here the gap in "we pretend they are there in order to better describe ?????" cannot be filled. I want to make an extremely tentative and undeveloped proposal about how to understand these contexts within the spirit of the make-believe approach.
Often the point of uttering S in a make-believe spirit is to (seriously) advance a game-induced content. Sometimes, though, the point is to map out the contours of the inducing game: e.g., to launch a game, or consolidate it, or make explicit some consequence of its rules, or extend the game by adjoining new rules, or urge the adoption of one proposed new rule rather than another, or articulate a norm implicitly guiding rule choice.[53] Examples of these activities in mathematics and elsewhere:
Launching: [In tag] "that was no ordinary clap on the back, you're IT!!!" [In math] "why do you say that -1 lacks a square root? aren't you forgetting our old friend i?"
Consolidating: [In tag] "if the IT person tags you anywhere on your body, you become IT" [In math] "remember, functions are arbitrary assignments."
Explicitating: [In tag] "unless you find someone to tag, you're IT for as long as the game lasts" [In math] "did you realize that .999999.... is no different from 1?"
Extending: [In tag] "if the IT person tags two people at once, they're both IT until one of them tags someone else" [In math] "it's not only intervals that have something worth calling a length, Borel sets have them too."
Urging: [In tag] "there will be fewer interruptions if whoever is IT gets to pick their replacement when they leave" [In math] "let's accept the axiom of determinacy because that way every set of real numbers comes out measurable."
Articulating: [In tag] "the trouble with that rule is, it should always be common knowledge who is IT" [In math] "the trouble with determinacy is, we want to have as many sets as the iterative conception allows"[54]
This last example allows me to illustrate how the "gameskeeping" conception of mathematics might be able to cope with phenomena that a Quinean is bound to find mysterious. Maddy in her recent Naturalism in Mathematics notes that Quine, in keeping with his picture of mathematics as continuous the rest of "total science," is led to conclusions very much at odds with the mathematical scientists he is seeking to emulate. His idea in a nutshell is that in set theory, as elsewhere in science, we should keep our ontology as small as practically possible. He is prepared to
recognize indenumerable infinites only because they are forced on me by the simplest known systematizations of more welcome matters. Magnitudes in excess of such demands, e.g., bethw or inacessible numbers, I look upon only as mathematical recreation and without ontological rights. Sets that are compatible with [Godel's axiom of constructibility] afford a convenient cut-off...[55].
Such an approach is valued as "inactivat[ing] the more gratuitous flights of higher set theory..." The consensus among set-theorists is of course pretty much the opposite. Cardinals the size of bethw are not even slightly controversial -- they are guaranteed by axioms everyone accepts -- and inaccessibles are considered quite innocent except by the lonely few who suspect that ZF is inconsistent; its consistency is deducible in ZF from the existence of an inacessible. As for Godel's axiom of constructibility, it has been widely criticized - including by Godel himself - as much too restrictive. Set-theorists have wanted not only to avoid restrictive axioms like constructibility, but to run as far as possible in the other direction, countenancing as fully packed a set-theoretic universe as the iterative conception permits.
If Quine's picture of set theory as something like abstract physics cannot make sense of the field's plenitudinarian tendencies, can any other picture do better? Well, clearly one is not going to be worried about multiplying entities if the entities are not assumed to really exist. But we can say more. The likeliest approach if the set-theoretic universe is make-believe would be (A) to articulate the clearest intuitive conception possible and then, (B) subject to that constraint, let all hell break loose.
Regarding (A), some sort of constraint is needed or the clarity of our intuitive vision will suffer. This is the justification usually offered for the axiom of foundation, which serves no real mathematical purpose but forces sets into the familiar and comprehensible tower structure. Without foundation there would be no possibility of "taking in" the universe of sets in one intellectual glance, as it were.
Regarding (B), it helps to remember that sets come in "originally" to improve our descriptions of non-sets, e.g., there are infinitely many Xs iff the set of Xs has a proper subset X' such that the members of X and X' are paired off by some 1-1 function (another set). Given that the notion of "infinitely many" is topic neutral -- the Xs do not have to meet some special "niceness" condition for it to make sense to ask whether there are or are not infinitely many of them - it would be counterproductive to have "niceness" constraints on when the Xs are going to count as bundleable together into a set, except to the extent that such contraints are needed to maintain consistency. It would be still more counterproductive to impose "niceness" constraints on the 1-1 functions; when it comes to infinitude, one way of pairing the Xs off 1-1 with just some of the Xs seems as good as another.
So much concerning the "original" applications of sets to talk about non-sets. But it would not be surprising if the anything-goes attitude at work here were to reverberate upward to contexts where the topic is sets. Just as we don't want to tie our hands unnecessarily in applying set-theoretic methods to the matter of whether there are infinitely many stars, we don't want to tie our hands either in considering whether there are infinitely many sets of stars. A case can thus be made for (imagining there to be) a plenitude of sets of stars, and a master set gathering all the star-sets together; and a plenitude of 1-1 functions from the master set to its proper subsets to ensure that if the former is infinite, there will be a function on hand to witness the fact. This perhaps gives the flavor of why the preference for a universe as "full" as possible is not terribly surprising on a gameskeeping conception of the theory of sets.
Bibliography
Alston, W. 1958. "Ontological commitment," Philosophical Studies, Vol. 9, No. 1, pp. 8-17
Burgess, J. & G. Rosen, 1997. A Subject With No Object (Oxford: Clarendon)
Cohen, J. 1997. "The Arc of the Moral Universe," Philosophy & Public Affairs 26, No. 2, pp. 91-134
Davidson, D. 1980. "The Logical Form of Action Sentences," in Essays on Actions & Events (Oxford: Oxford University Press)
Davidson, D. 1978. "What metaphors mean," in Sacks 1979
Davidson, D. & G. Harman, 1975. The Logic of Grammar (Encino: Dickenson)
Davies, M. & L. Humberstone, 1980. "Two Notions of Necessity," Philosophical Studies 38, pp. 1-30
Etchemendy, J. 1990. The Concept of Logical Consequence (Cambridge, MA: Harvard University Press)
Field, H. 1989. "Platonism for Cheap? Crispin Wright on Frege's context principle," in Realism, Mathematics, & Modality (Oxford: Basil Blackwell)
Hahn, L. & P. Schilpp (eds.) 1986. The Philosophy of W.V. Quine (La Salle, IL: Open Court)
Hills, D. forthcoming. "Aptness and Truth in Metaphorical Utterance," Philosophical Topics
Jackson, F. 1979. "On Assertion and Indicative Conditionals," Philosophical Review 88, 565-589
Kaplan, D. 1989. "Demonstratives," in J. Almog, J. Perry, & H. Wettstein, ed., Themes from Kaplan (New York: Oxford University Press)
Lewis, D. 1992. "Critical Notice of Armstrong, D.M., A Combinatorial Theory of Possibility," Australasian Journal of Philosophy 70, pp. 211-224
Lewis, D. 1986. On the Plurality of Worlds (New York: Basil Blackwell)
Maddy, P. 1997. Naturalism in Mathematics (Oxford: Clarendon)
McGee, V. 1997. "How We Learn Mathematical Language," Philosophical Review 106, pp. 35-68
Melia, J. 1995. "On what there's not," Analysis, Vol. 55, No. 4, pp. 223-229
Moran, R. 1989. "Seeing and Believing: Metaphor, Image, and Force," Critical Inquiry, Vol. 16, pp. 87-112
Ortony, A. 1993. Metaphor and Thought, second edition (Cambridge: Cambridge University Press)
Plantinga, A. ed. 1965. The Ontological Argument (Garden City, NY: Doubleday)
Prior, A. 1976. Papers in Logic and Ethics (Amherst: University of Massachusetts Press)
Putnam, H. 1971. Philosophy of Logic (New York: Harper & Row)
Quine, W.V. 1948. "On what there is," Review of Metaphysics, Vol. II, No. 5, reprinted in Quine 1953
Quine, W.V. 1953. From a Logical Point of View (Cambridge, MA: Harvard University Press)
Quine, W.V. 1960. Word & Object (Cambridge: MIT Press)
Quine, W.V. 1966. "Propositional Objects," in Ontological Relativity and Other Essays (New York: Columbia University Press)
Quine, W.V. 1978. "A Postscript on Metaphor," in Sacks 1978
Quine, W.V. 1986. "Reply to Parsons," in Hahn & Schilpp 1986
Sacks, S., ed. 1978. On Metaphor (Chicago: University of Chicago Press)
Salmon, N. 1989. "The Logic of What Might Have Been," Philosophical Review, Vol. 98, pp. 3-34
Sommer, E. & D. Weiss, 1996. Metaphors Dictionary (New York: Visible Ink Press)
Walton, K. 1993. "Metaphor and Prop Oriented Make-Believe," European Journal of Philosophy 1, pp. 39-57
Wright, C. 1983. Frege's Conception of Numbers as Objects (Aberdeen: Aberdeen University Press)
Yablo, S. 1996. "How in the World?," Philosophical Topics 24, pp. 255-286
Yablo, S. 1998. "Does Ontology Rest on a Mistake?," Proceedings of the Aristotelian Society, supp. vol. 72, pp. 229-262
[1] David Hills, Ken Walton, Mark Crimmins, Ralph Wedgwood, Ned Hall, John O'Leary-Hawthorne, Peter van Inwagen, Stephen Schiffer, David Chalmers, Kent Bach, Laura Bugge, Sol Feferman, Thomas Hofweber -- thanks! A scattered 15% of the paper is taken from Yablo 1998.
[2] The classic formulation is Hilary Putnam's: "quantification over mathematical entities is indispensable for science...; therefore we should accept such quantification; but this commits us to accepting the existence of the mathematical entities in question" (1971, 57).
[3] A possible exception is Arthur Prior in "Entities," who comments: "This is very elementary stuff -- I am almost tempted to apply the mystic word 'tautological' -- and I apologise for so solemnly putting it forward in a learned journal. But I do not think it can be denied that these things need to be said. For there are people who do not agree with them..." (1976, 26)
[4] Etchemendy 1990.
[5] Compare a non-platonic bridge principle like (R) a region is populated iff it contains people," Should it be discovered that there are no people (everyone but you is a holographic projection, and you are a deluded angel) we would willingly conclude, on the basis of (R), that no regions are populated. This is (one of many reasons) why friends of the population principle can afford to be ontologically complacent - one of many reasons why they do not stay up late at night worrying about the existence of people.
[6] The problem stated a little more carefully is how to deal with the following: on the one hand, we feel entitled to the bridge principles regardless of the empirical facts (experience doesn't matter to truth); while on the other hand, we think that the empirical facts are highly relevant to whether the mentioned objects exist (experience does matter to ontology); while on the third hand, we regard the bridge principles as almost certainly false if they do not exist (ontology matters to truth).
[7] To their literal truth, that is; see below.
[8] Cf. Field in a critical response to Wright: "the conceptual truth is [not "the number of As= the number of Bs iff there are as many As as Bs" but] rather "if numbers exist, then..." (Field 1989, 169).
[9] Perhaps more can be said: unless there is water, my idea of water cannot be fully clear.
[10] Another example: Suppose I want to distinguish the classical notion of validity from the circumscriptive notion. (The latter allows me to infer "there are exactly two cows" from "Bossie is a big cow and Elsie is a cow that is not big.") An "intrinsic" characterization of the difference might not be easy to devise; some sort of allusion to models seems unavoidable. Why not the following? An argument is classically valid iff, bracketing any worries about the existence of models, it has no countermodels; an argument is circumscriptively valid iff, bracketing any worries about the existence of models, none of its countermodels is a minimal model of its premises. Again, I can explain the notion of a Dedekind-infinite as opposed to numerically-infinite plurality by saying: there are D-infinitely many Fs iff assuming mathematical objects, there is a 1-1 function from all the Fs to only some of the Fs; there are N-infinitely many Fs iff assuming mathematical objects, there is a 1-1 function from the natural numbers into the Fs.
[11] I am grateful here to Peter van Inwagen. and, for the related idea that models are called on to explain validity-facts, to Kent Bach.
[12] See an earlier footnote.
[13] E.g., let P1 = Fa, P2 = Gb, and P3 = -Fb. Then minimal models of {P1,P2,P3} have two elements each, while those of {P1,P2} have just one.
[14] Lewis 1992.
[15] This is a particular theme of Paul Boghossian's paper "Status of Content."
[16] Cf. McDowell on yesterday's rainstorm.
[17] Contrast the population principle: region R is populated iff there are people in it. Here a determinate conception of people isn't itself enough to make for an objective fact of the matter about which regions are populated.
[18] Walton 1993, 40-1.
[19] Yablo 1996 argues that worlds are metaphorical. Is it really necessary to use metaphor in explaining how metaphor works? I have no idea but it would would be fine by me if it were.
[20] A lot of metaphors are, literally understood, impossible: "I am a rock." Assuming we want a non-degenerate region on the left, the space of worlds should take in all "ways for things to be," not just the "ways things could have been." The distinction is from Salmon 1989.
[21] I am indebted to Melia 1995. Following the example of Quine, I will be using "metaphor" in a very broad sense; the term will cover anything exploiting the same basic semantic mechanisms as standard "Juliet is the sun"-type metaphors, no matter how banal and unpoetic.
[22] Why not a primitive "2.4-times-as-many" predicate? Because 2.4 is not the only ratio in which quantities can stand; "we will never find the time to learn all the infinitely many [q-times-as-many] predicates," with q a schematic letter taking rational substituends, much less the r-times-as-long predicates, with r ranging schematically over the reals (Melia 1995, 228). A fundamental attraction of existential metaphor is its promise of ontology-free semantic productivity. How real the promise is -- how much metaphor can do to get us off the ontology/ideology treadmill -- strikes me as wide open and very much in need of discussion.
[23] Compare Quine on states of affairs: "the particular range of possible physiological states, each of which would count as a case of [the cat] wanting to get on that particular roof, is a gerry-mandered range of states that could surely not be encapsulated in any manageable anatomical description even if we knew all about cats...Relations to states of affairs,...such as wanting and fearing, afford some very special and seemingly indispensable ways of grouping events in the natural world" (Quine 1966, 147). Quine sees here an argument for counting states of affairs into his ontology. But the passage reads better as an argument that the metaphor of states of affairs allows us access to theoretically important contents unapproachable in any other way. See also Lewis on counterfactuals: "It's the character of our world that makes the counterfactual true -- in which case why bring the other worlds into the story at all? .....it is only by bringing the other worlds into the story that we can say in any concise what character it takes to make the counterfactual true" (Lewis 1986, 22).
[24] Davidson 1978; Max Black in Ortony 1993; Moran 1989, 108.
[25] Moran 1989, 90.
[26] Similarly with Quine's cat example: the gerrymandered anatomical description even if available could never do the cognitive work of "What Tabby wants is that she gets onto the roof."
[27] See Davidson & Harman 1975. The underlying motivation had to do less with entailment than constructing axiomatic truth theories for natural language.
[28] A question rarely addressed is why this presentational advantage should seem to argue for the truth of the quantificational rendering, as opposed to just its naturalness and helpfulness vis-a-vis audiences like ourselves. Is it that the naturalness and helpfulness would be a miracle if there were nothing out there to answer to the platonic quantifiers? I would like to see an argument for this. I suspect that there are very few putative object-types, however otherwise disreputable, that couldn't be "legitimated" by such a maneouvre.
[29] Davidson 1978, 44.
[30] Davidson 1978, 29. Davidson would have no use for even the unsettled sort of metaphorical content about to be proposed.
[31] David Hills's phrase, and idea.
[32] This of course marks a difference with Davidson.
[33] Thus, each in its own way, "Juliet is the sun," "Eternity is a spider in a Russian bathhouse," and "The state is an organism."
[34] Examples: An apparition assures Macbeth that "none of woman born" shall harm him; the phrase's meaning hangs in the air until Macduff, explaining that he was "from his mother's womb untimely ripped," plunges in the knife. Martin Luther King Jr. told his followers that "The arc of the moral universe is long, but it bends toward justice"; recent work by Josh Cohen shows how specific a content can be attached to these words. A growing technical literature on verisimilitude testifies to the belief that "close to the truth" admits of a best interpretation.
[35] Indeterminacy is also possible about whether I am advancing a content at all, as opposed to articulating the rules of some game relative to which contents are figured, ie., doing some gameskeeping. An example suggested by David Hills is "there are continuum many spatiotemporal positions," uttered by one undecided as between the substantival and relational theories of spacetime. One might speak here of a fifth grade of metaphorical involvement, which -- much as the third grade leaves it open what content is being expressed -- takes no definite stand on whether the utterance has a content.
[36] "When it was reported that Hemingway's plane had been sighted, wrecked, in Africa, the New York Mirror ran a headline saying, "Hemingway Lost in Africa," the word "lost" being used to suggest he was dead. When it turned out he was alive, the Mirror left the headline to be taken literally" (Davidson 1978). I suspect that something like this happens more often than we suppose, with the difference that there is no conscious equivocation and that it is the metaphorical content that we fall back on.
[37] The intuition here comes out particularly clearly in connection with Walton's account of metaphor; I need first to understand what S literally means, if I am to pretend that that meaning obtains in hopes of calling attention to the conditions that legitimate the pretense.
[38] I do not see why the weight of a sentence's metaphoricality should always be borne by particular words. But let's not get into that issue here.
[39] Apparently it is; my dictionary gives it the meaning "pregnant." The point is that my use of it in the game owes nothing to this meaning or any other, or even to "gravid"'s being a word.
[40] Notwithstanding an increasing willingness in recent years to consider them with a straight face. Prior, "Entities," deserves a lot of the credit for this: "...what we might call Bosanquetterie sprawls over the face of Philosophy like a monstrous tumour, and on the whole the person who maintains that virtue is not square must count himself among the heretics. The current dodge or 'gambit' is to say that the question whether virtue is or is not square just doesn't arise, and it is astonishing what a number of questions modern philosophers have been able to dispose of by saying that they just don't arise. Indeed it is hardly too much to say that the whole of traditional philosophy has disappeared in this way, for among questions that don't arise are those which, as it is said, nobody but a philosopher would ask" (26).
[41] Events are an important exception!
[42] Yablo 1998 has details.
[43] For a sense of why "P iff Q" should have a different use than "Q iff P," see Jackson on "if" and "only if" in his 1979.
[44] Alston 1960; Wright 1983, pp. 31ff.
[45] Quine 1960, 214.
[46] A minimal model of P is one with no proper submodels that also models P.
[47] Davies & Humberstone 1980.
[48] Kaplan 1989.
[49] "It holds fixedly that S" corresponds more or less to "no matter how matters actually stand, it's still the case that S." (There are nuances here that I'm ignoring.) Someone might say: doesn't that paraphrase put the lie to the idea that fixedly is not expressible in English?
[50] Many apparent counterexamples have been adduced. Kaplan himself cites Thomason: "never put off till tomorrow what you can do today." And consider this from a New Yorker cartoon: "of course, that was long ago now; but at the time it felt like the present."
[51] This phenomenon was brought to prominence recently by Davidson's first-orderizing of adverb-dropping inferences. He maintains that "she sang Kly" entails "she sang" because "there was a singing with her as agent which was K" first-order entails "there was a singing with her as agent."
[52] This is as good a place as any to say that a more complicated definition is often given.
[53] I suspect that a "gameskeeping" story will be easier to tell with sets and numbers than events and properties; I hope so, anyway. I look to difficulties with autonomous contexts to provide a natural brake on the creeping metaphoricalism that might otherwise threaten.
[54] See Maddy 1997. The tower of sets is made maximally "wide" by replacing ZF's axiom schemata with 2nd order axioms. See McGee 1997 for an axiom intended to make it maximally "tall."
[55] Quine 1986