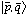 for classical particles. After a time t, the quantum-mechanical propagation of
a wave-packet is convolved with the original state as a measure of the extent
to which its motion approximates a periodic orbit with that period:
for classical particles. After a time t, the quantum-mechanical propagation of
a wave-packet is convolved with the original state as a measure of the extent
to which its motion approximates a periodic orbit with that period:
by
A formula analogous to Gutzwiller's trace formula is derived for computing a semi-classical approximation to the quantal E-t plot. This formula is then tested numerically for the Nelson Hamiltonian; its results are seen to approximately equal the exact quantum-mechanical values.
Submitted to the Department of Physics
in partial fulfillment of the requirements for the degree of:
at the
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
May 1995
(c) Steven G. Johnson, MCMXCV. All rights reserved.
The author hereby grants to MIT permission to reproduce and to distribute publicly paper and electronic copies of this thesis document in whole or in part, and to grant others the right to do so.
The E-t plot (a graph of the energies of orbits versus their periods) is an important tool for characterizing the periodic trajectories of classical systems. It illustrates features such as bifurcations, stability and instability, and other useful information about both the chaotic and regular dynamics in the system. Thus, when we investigate how classical behavior, especially classically chaotic behavior, arises out of a quantum system in the classical limit, it is useful to examine how the E-t plot evolves from the quantum picture.
A way to compute purely quantum-mechanical E-t plots has been developed1 which is described in the next section. It yields a formula Q(E,t) for the quantal E-t plot in terms of the energy eigenvalues of the quantum system. The results produced by this equation (e.g. figure 2 later on) display complicated features. Between neighboring families of classical orbits, for example, there are interesting interference patterns whose connection to the classical system is not at all clear. In order to investigate the relationship between these quantum and classical treatments of chaotic systems, it seems fruitful to examine the E-t plot in the context of semi-classical mechanics. At this mid-point between quantum and classical mechanics, one is better equipped to understand what features of the quantum problem are most essential in giving rise to the classical behaviors. Therefore, in this paper a semi-classical form for Q(E,t) is developed which describes the quantum-mechanical plot in terms of classical quantities. Then, in order to check the validity of this equation, it is used to analyze a particular system and its results are compared to the exact quantum results. They are seen to agree, demonstrating the validity of this approach.
The quantum-mechanical analogue of the classical E-t plot can be thought
of as simply the substitution of coherent states
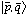 for classical particles. After a time t, the quantum-mechanical propagation of
a wave-packet is convolved with the original state as a measure of the extent
to which its motion approximates a periodic orbit with that period:
for classical particles. After a time t, the quantum-mechanical propagation of
a wave-packet is convolved with the original state as a measure of the extent
to which its motion approximates a periodic orbit with that period:
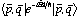 (1)
(1)This result is then Fourier transformed to substitute energy for time as a parameter, limited by a Gaussian around t = t (this is actually called a Gabor transform).
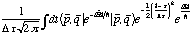 (2)
(2)Finally, in order to include all possible trajectories and periodic orbits, the trace is taken over the wave-packets. Using the fact that:
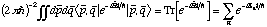 (3)
(3)the time integral in (2) is seen to become a simple Gaussian, and yields the following result for the exact quantal E-t plot in terms of the energy eigenvalues En:
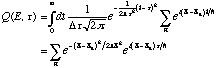 (4)
(4)Here, dE is related to dt by the relation dEdt=h. It should be noted that Q(E,t) is a complex number; the quantity which is actually plotted in figures 2 through 6 later on is the modulus of Q (or of its semi-classical analogue).
An important development in the study of semi-classical systems was the derivation of Gutzwiller's trace formula.2 This formula describes the energy eigenvalues of the quantum-mechanical system in terms of the classical periodic orbits:
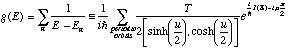 (5)
(5)Here, the function g(E) is expressed in terms of simple classical quantities for each periodic orbit: the period T, the stability index u, the action J around the orbit, and the Maslov index u. The stability index is enclosed in a sinh or a cosh depending on whether the orbit is hyperbolic or inverse hyperbolic.
This beautiful result is only a function of E, but it would be desirable if this function could somehow be limited in time to derive the quantal E-t plot. This would also solve the problem of convergence, since only a finite number of period orbits would need to be included in the sum. In fact, it is possible to do so, and it will be shown below that it is merely necessary to insert a Gaussian function of (t - t) into the trace formula to yield a semi-classical expression for Q(E,t).
The trace formula in (5) is a semi-classical approximation for the integral over q of the quantum Green's function G(qqE), given by:
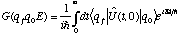 (6)
(6)
Here,
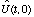 is the time evolution operator which takes any state at time 0 and yields the
evolution of that state at time t--its matrix element is taken with respect to
eigenstates of the position operator. Now, suppose a Gaussian (with a
normalization factor) is inserted into the integral of G(qqE) in order to limit
it in time. Into this expression a sum over the complete set of energy
eigenstates, |Psin>, can furthermore be inserted. The resulting
expression then simplifies since the time evolutions of such states are just
the original states plus a phase, yielding the following sequence of
expressions:
is the time evolution operator which takes any state at time 0 and yields the
evolution of that state at time t--its matrix element is taken with respect to
eigenstates of the position operator. Now, suppose a Gaussian (with a
normalization factor) is inserted into the integral of G(qqE) in order to limit
it in time. Into this expression a sum over the complete set of energy
eigenstates, |Psin>, can furthermore be inserted. The resulting
expression then simplifies since the time evolutions of such states are just
the original states plus a phase, yielding the following sequence of
expressions:
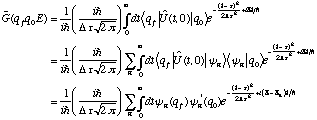 (7)
(7)If (7) is now integrated over all q = qf = q0, just as was done when g was derived from G in the trace formula, the result is simply found to be the quantal E-t function Q from (4):
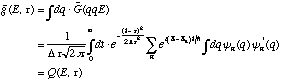 (8)
(8)This derivation, of course, only applies in the exact quantum-mechanical treatment. In order to derive the semi-classical formula for Q(E,t) analogous to (8), Gutzwiller's derivation of the trace formula for g(E) must be repeated with the single modification that the Gaussian-limited (7) is substituted for G(qqE).
The starting-point for deriving the semi-classical expression for Q will be Van Vleck's formula for the matrix entries of the time-evolution operator. This is derived by expanding Feynman's path integral around the stationary-phase (classical) paths, and is as follows:
 (9)
(9)Here, d is the dimension of position-space (half the dimension of the classical phase space), K is the number of conjugate points along the trajectory, and S is Hamilton's principal function, given by:
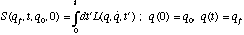 (10)
(10)This approximation is inserted into expressions (7) and (8) for Q, yielding:
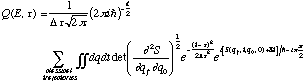 (11)
(11)
Now, the main contribution to the integral over t comes from the neighborhood
of time where the phase varies slowly. In regions where the phase varies
quickly with time, assuming that changes of S are large compared to
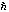 ,
the amplitude remains relatively constant while the phase changes
rapidly--thus, contributions from neighboring times in the integral tend to
cancel. So, the integrand is expanded around the time T when the phase is
stationary, which is given by:
,
the amplitude remains relatively constant while the phase changes
rapidly--thus, contributions from neighboring times in the integral tend to
cancel. So, the integrand is expanded around the time T when the phase is
stationary, which is given by:
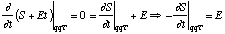 (12)
(12)
However,
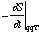 is just the energy of the classical path that goes from q back to q in time T.
Therefore, the conclusion is that T is simply the period of the classical path
with energy E which starts and ends at q. The amplitude of the integrand in
(11) is then evaluated at time T and the phase is Taylor-expanded to second
order around T. The value of the phase at time T is just a Legendre
transformation of S, and yields the action integral J around the path with
energy E:
is just the energy of the classical path that goes from q back to q in time T.
Therefore, the conclusion is that T is simply the period of the classical path
with energy E which starts and ends at q. The amplitude of the integrand in
(11) is then evaluated at time T and the phase is Taylor-expanded to second
order around T. The value of the phase at time T is just a Legendre
transformation of S, and yields the action integral J around the path with
energy E:
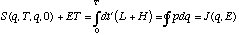 (13)
(13)Thus, the time integral in (11) simply becomes the following Gaussian integral (here, only the time-dependent terms are included):
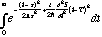 (14)
(14)
Let
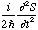 be denoted by a and
be denoted by a and
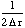 by b. Then, by completing the square and integrating using the standard
Fresnel/Gaussian integral, (14) becomes:
by b. Then, by completing the square and integrating using the standard
Fresnel/Gaussian integral, (14) becomes:
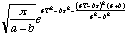 (15)
(15)
It is assumed that dt is chosen so that |b| is much smaller than
|a|, and the exponent in the above expression is expanded in that limit. This
is a reasonable assumption, since the derivatives of S were assumed earlier to
be large compared to
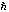 ,
and a time resolution dt for Q(E,t) that is many orders of
magnitude smaller than 1 is not likely to be desired. Also, a - b in the
amplitude of (15) may be approximated by a, since this only changes the
amplitude by
,
and a time resolution dt for Q(E,t) that is many orders of
magnitude smaller than 1 is not likely to be desired. Also, a - b in the
amplitude of (15) may be approximated by a, since this only changes the
amplitude by
 .
Combining all of these approximations for (15) and substituting them back into
(11), the expression becomes:
.
Combining all of these approximations for (15) and substituting them back into
(11), the expression becomes:
 (16)
(16)Note that this is just what would have resulted if the real part of the exponent in (14) had been evaluated at t = T immediately, which makes sense since it is slowly varying with time compared to the phase. At this point, the Gaussian in t can be taken out of the integral in (16), leaving inside exactly what would have been there if the Gaussian hadn't been put into (7) in the first place. That is, what is left inside the integral is equivalent to simply integrating G(qqE). But this, of course, is precisely where Gutzwiller's trace formula comes from, and so the remaining integral simplifies to (5) except that the Gaussian in t is inside the sum over the periodic orbits (with the normalization for the Gaussian inserted in front). Thus, the following semi-classical expression for Q(E,t) is finally arrived at:
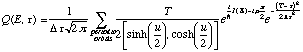 (17)
(17)Formula (17) can also be expressed in terms of the classical monodromy matrix, M. This matrix describes how infinitesimal changes in the initial conditions of an orbit will be reflected after the system has evolved for one period of the orbit:
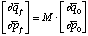 (18)
(18)
In a two-dimensional system, M will have two pairs of eigenvalues, each pair
having a product of one. The first pair of eigenvalues are both unity, and
correspond to displacements along the orbit. If the orbit is unstable, the
other two eigenvalues are either positive or negative
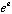 and
and
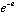 ,
depending upon whether the orbit is "hyperbolic" or "inverse hyperbolic." Here,
u is the stability index from the trace formula. Then, in the first case:
,
depending upon whether the orbit is "hyperbolic" or "inverse hyperbolic." Here,
u is the stability index from the trace formula. Then, in the first case:
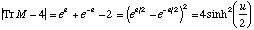 (19)
(19)And, in the second case of the orbit being inverse hyperbolic, a similar result follows:
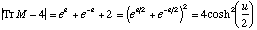 (20)
(20)Thus, comparing (19) and (20) with (18), this final expression for the quantal E-t plot is obtained in terms of the monodromy matrix M:
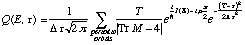 (21)
(21)It should be noted that, like the Gutzwiller trace formula itself, this equation is not valid near bifurcation points in the E-t plane, where it diverges (the trace of M goes to 4).
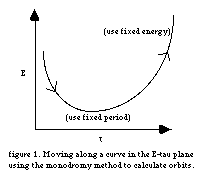
In order to perform calculations with equation (21), it was necessary to be able to calculate the periodic orbits of a system at various energies and periods. The main device that was used to compute these (discretized) periodic orbits was the monodromy method.3 This, along with the other numerical calculations described later, was performed using a C program for the analysis of periodic orbits developed by the author. Given a periodic orbit at a particular energy or period, the monodromy method is a way of computing another periodic orbit (usually in the same family) at a nearby energy or period. Each iteration of the monodromy method yields a better approximation to the desired orbit and convergence is very rapid. This method can operate with either the energy or the period of the orbit fixed, varying both the locations of the points in the orbit and its period or energy, respectively. Thus, given one orbit as a starting point, it is possible to move along a curve in the E-t plot for the system, calculating any desired orbit--working at either fixed energy or fixed period depending upon whether the curve is more nearly vertical or horizontal, respectively (see figure 1).
A brief description of the monodromy method for fixed period is as follows.
Given a set period and number of points, the equations of motion can be
written, discretized, in terms of a fixed time step e. The
points on the orbit are calculated as deviations (
 ,
,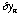 )
from a known approximate periodic orbit (
)
from a known approximate periodic orbit (
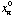 ,
,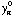 ),
often a periodic orbit for a slightly different period. The linearized,
discretized equations for the deviations can then be expressed as a matrix
equation of the following form:
),
often a periodic orbit for a slightly different period. The linearized,
discretized equations for the deviations can then be expressed as a matrix
equation of the following form:
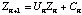 (22)
(22)Here, Un is a 4x4 matrix and Cn is a column vector expressing the discretized equations in terms of the column vectors Zn, where:
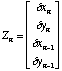 (23)
(23)Equation (22) can be successively applied to yield Zn+1 from Z1 in terms of a new matrix Lambdan+1 and column vector Gamman+1, where:
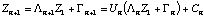 (24)
(24)From (24), the following recursive relations are seen to hold for Lambdan+1 and Gamman+1, along with the associated boundary conditions:
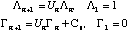 (25)
(25)If the orbit has been discretized into N points, these relations can be applied N times to yield LambdaN+1 and GammaN+1, which give ZN+1 by equation (24). However, if the orbit is to be periodic, then ZN+1 must equal Z1, yielding the condition:
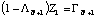 (26)
(26)This matrix equation can be inverted to find Z1, which can then be used to calculate all Zn by equation (24). These deviations can then be added to the original points to find a new set of initial points, which can be plugged back into the monodromy method as a new starting orbit. After a few iterations, the resulting trajectory will have converged to the exact periodic orbit with the desired period. The criterion for stopping the iterations, in terms of some small threshold relative to the floating point precision being used, is:
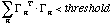 (27)
(27)Once this point has been reached, it is apparent from equation (24) that LambdaN+1 is equivalent to the monodromy matrix discussed earlier, since multiplying it by a deviation Z1 in the initial point of the orbit yields the deviation after one period, ZN+1. Of course, these deviations are expressed in terms of the deviations in the positions of the first two points, rather than in the position and momentum of the first point as was done in equation (18). However, it is clear that the eigenvalues of the two matrices must be the same, and thus that the trace of LambdaN+1 is equal to the trace of the monodromy matrix needed by equation (21). The energy of the orbit can also be calculated, since the points and time step are known, simply by averaging the kinetic and potential energies for each pair of points in the trajectory.
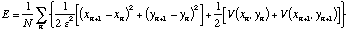 (28)
(28)
Applying the monodromy method in the situation where the energy is to be held
fixed and the period varied is more difficult. It is necessary, however, since
the families of orbits to be explored in the next section mostly consist of
nearly vertical lines in the E-t plane. Essentially, what is done is to
hold the energy of the first pair of points constant, and modify the
discretized equations so that variations
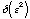 in the time step squared are also allowed. The result of this, in the end, is
that a 5x5 matrix has to be inverted to find the variation in the period as
well as in initial points, instead of the 4x4 matrix of equation (26). The
basic procedure followed is the same, however.
in the time step squared are also allowed. The result of this, in the end, is
that a 5x5 matrix has to be inverted to find the variation in the period as
well as in initial points, instead of the 4x4 matrix of equation (26). The
basic procedure followed is the same, however.
Expression (21) for the semi-classical E-t plot, having been derived theoretically, was then compared numerically to the exact quantum-mechanical results for a particular two-dimensional system, the Nelson Hamiltonian:
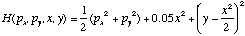 (29)
(29)This Hamiltonian was chosen because both exact energy eigenvalues4 and detailed classical analyses5 were available for it. Given the energy eigenvalues, it was straight-forward to write a short C program to calculate the exact quantum-mechanical E-t plot using equation (4). However, calculating the semi-classical approximation by equation (21) was more difficult than the exact quantum case, since it involved computation of the periodic orbits, their stabilities, and so on, at many different energies and periods.
The computation of periodic orbits was performed using the monodromy method described earlier. The monodromy method requires a starting point, though--at least one orbit on a curve in the E-t plot. However, this orbit need not be exactly correct; it only needs to be close enough to a real periodic orbit that the monodromy method is able to converge. As it turns out, the monodromy method is robust enough to converge when only a very rough approximation of a real orbit is given to it, along with the initial energy and period. This was easily done, since graphs of the families of orbits in the E-t plane and many of their associated orbits were available for the Nelson potential.5 It was necessary merely to copy a few points off the graph of an orbit, feed them into the program, and let the monodromy method compute the exact orbit. Then, additional points could be added by linear interpolation and the monodromy method run again. In this way, orbits on several curves in the E-t plot were computed with a small time step (1000 data points). Other families of orbits could then be found because they were connected to the known orbit families via isochronous branching, such as the two orbits that branch upwards from a single point in figure 1. Using the monodromy method with fixed energies, it was possible to move down the orbit to the branching point, at which point one could move horizontally to the other orbit by using the monodromy method with fixed periods.
Given a periodic orbit at a particular energy, it is then necessary to calculate the quantities used in the trace formula (21). Both the period and the monodromy matrix M are returned by the monodromy method itself once it has converged, so the only things remaining to be calculated are the action J and the Maslov index u. J is computed simply by performing a discretized version of (13). As it turns out, the Maslov index that appears in the trace formula is the winding number of the stable or unstable manifolds.6 This was computed using Fortran code adapted from a program supplied by Daniel Provost.7
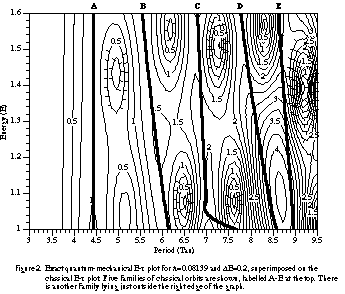
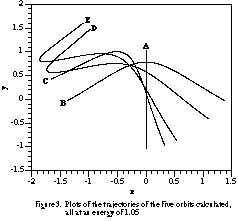
Given the machinery developed above, it then remained to choose an appropriate portion of the E-t plane, using the known classical E-t plots and orbits,5 in which to compute the quantal E-t plot. There were several criteria for this selection. First, it had to be a region for which almost all the families of periodic orbits had been calculated. Second, it could not contain any bifurcation points or equation (21) would diverge. Third, it should be in a region where the quantal plot displays interesting interference patterns, in order to see whether the semi-classical plot contains the same features. Such a region was chosen, and the classical and exact quantum-mechanical E-t plots for it are shown in figure 2. Orbits A through E were calculated by the methods described above, and are displayed in figure 3. One of the families of orbits just to the right of the region was not computed; this allows the effect of an orbit's omission to be seen in the semi-classical plot of (21).
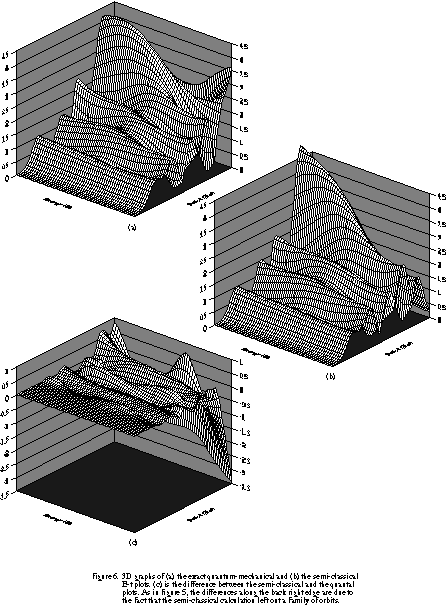
Once an orbit in each desired family had been calculated, it was then straight-forward to compute the semi-classical E-t plot from the trace formula (21) derived earlier. For each energy, the monodromy method (operating at fixed energy) was used to compute the orbits in each family at that energy, along with their periods and monodromy matrices. The previously calculated Maslov indices could be used unchanged, since they are a characteristic of a family of orbits and do not vary with energy. The action, J, was found using formula (13) as described earlier. Finally, the sum in equation (21) could be performed and the modulus of Q(E,t) was found for each desired energy and time. These values are plotted in figure 4, and the difference between the semi-classical and quantum results is shown in figure 5. The differences are quite small, except in the far right portion of the graph where the effects of the missing orbit are dramatically displayed. It is somewhat easier to obtain a qualitative understanding of the magnitude of the differences between the exact quantum-mechanical and the semi-classical results from the three-dimensional versions of these plots, shown in figure 6.


The classical E-t plot characterizes much of the structure of a dynamical system, displaying the relationships between various families of periodic orbits. Its quantum-mechanical analogue, Q(E,t), describes the analogous information in terms of the propagation of coherent wave packets, and exhibits a complicated structure of interference between different families of orbits (see figure 2). The way in which this structure is linked to the classical picture has been found through the development of a semi-classical trace formula similar to the Gutzwiller trace formula, connecting Q(E,t) to the periodic orbits of the classical system. Unlike the Gutzwiller formula, however, the trace formula derived here does not present any difficulty in the convergence of an infinite sum over the orbits--the problem of convergence is circumvented by limiting the sum with a Gaussian distribution around a particular period. Unfortunately, the problem of divergence at bifurcation points remains, and is unlikely to be solved without a tedious extension of the approximations used to higher orders in h. Nevertheless, the semi-classical trace formula has been successfully applied to the study of a particular system, that of the Nelson Hamiltonian, in which the exact quantum-mechanical solution was known. With the aid of C code developed to find, analyze, and manipulate the periodic orbits of a classical system, the semi-classical trace formula (21) was computed and compared to the exact results. The two answers were seen to approximately agree, and moreover the semi-classical plot displayed the same amplitudes and complicated interference structure seen in the quantum results.