Studies in Two-Factor Authentication: Solution
By Brandon Avila
Answer:
BOTNET
As clued by the flavor text, this puzzle has to do with factoring primes in the complex plane. The image is a 250x250 section of the first quadrant in the complex plane beginning at (0, 0) in the bottom left corner. Each black dot represents a Gaussian prime (a prime number in the ring of Gaussian integers), and each colored dot represents a composite number with exactly two factors.
For each color (red through purple), the composite numbers are factored, and their factors are connected pairwise in the plane by a line as follows:
B: Red

43 + 80i = (8 + 3i)(8 + 7i)
76 + 65i = (8 + 3i)(11 + 4i)
68 + 87i = (8 + 5i)(11 + 4i)
58 + 103i = (8 + 5i)(11 + 6i)
46 + 125i = (8 + 7i)(11 + 6i)
O: Orange

6 + 3i = (2 + i)(3)
12 + 3i = (4 + i)(3)
10 + 11i = (4 + i)(3 + 2i)
4 + 7i = (2 + i)(3 + 2i)
T: Yellow

47 + 140i = (8 + 7i)(12 + 7i)
79 + 100i = (10 + 7i)(10 + 3i)
N: Green

11 + 24i = (4 + i)(4 + 5i)
19 + 34i = (6 + i)(4 + 5i)
31 + 36i = (6 + i)(6 + 5i)
E: Blue
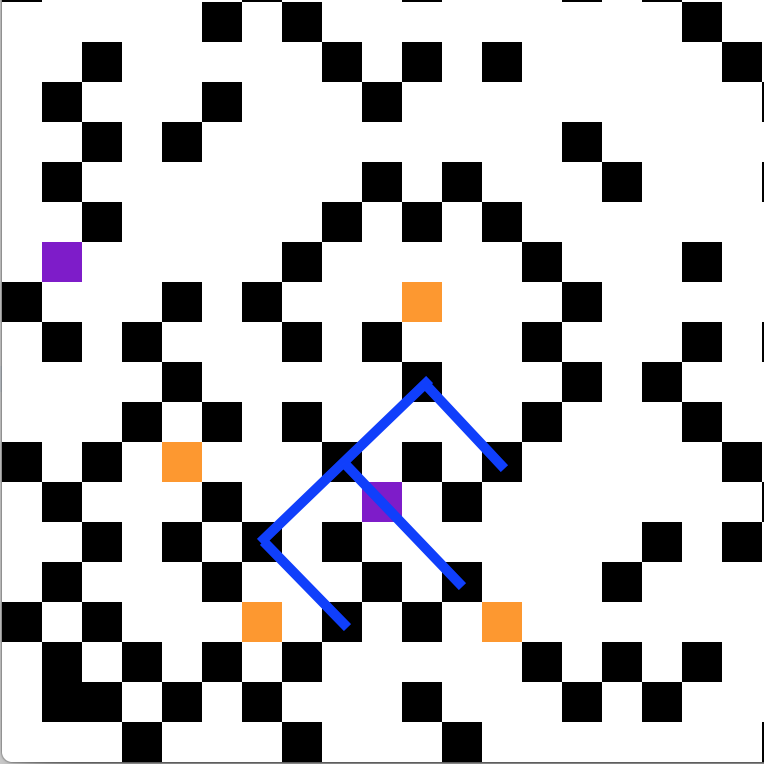
15 + 104i = (6 + 5i)(10 + 9i)
33 + 58i = (6 + 5i)(8 + 3i)
57 + 178i = (10 + 9i)(12 + 7i)
60 + 109i = (11 + 4i)(8 + 7i)
T: Purple

1 + 12i = (1 + 2i)(5 + 2i)
9 + 6i = (3 + 2i)(3)
Taken in order, these letters spell out the solution, BOTNET.