The solutions to submetas that feed into this puzzle are as follows:

• EXOSKELETON
• BIOFUEL TORCH
• BACKUP PLAN

Each set of rewards on the bulletin boards can be used to construct a graph connecting puzzles.

For the Scout floorplan, nodes are rooms, and edges are doorways (with door opening direction specifying edge direction):

For the Build block diagram, nodes are blocks and edges are output-to-input connections:

For the Deploy round, Raspberry Pi-powered “radios” were installed around campus with a two-channel selector and a push-to-talk button:

Each radio would “broadcast” to a channel on one or more radios (potentially including itself), with asymmetric transmissions (just because radio A could hear radio B did not mean that radio B could hear radio A). Each radio represents a node, and edges are directed links from a transmitting radio to the radio(s) that can receive its transmission.

The collected rewards then reduce to directed graphs:

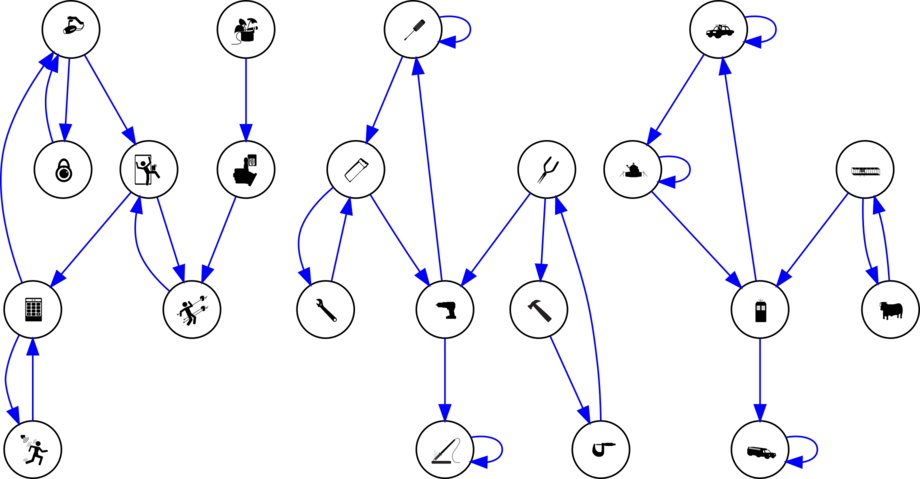
Next, notice that each graph has the same number of edges as the meta answer for that round has letters. In fact, each graph actually contains a unique Eulerian path. The Eulerian paths provide an ordering over edges, so that they may be labelled with the meta answer:

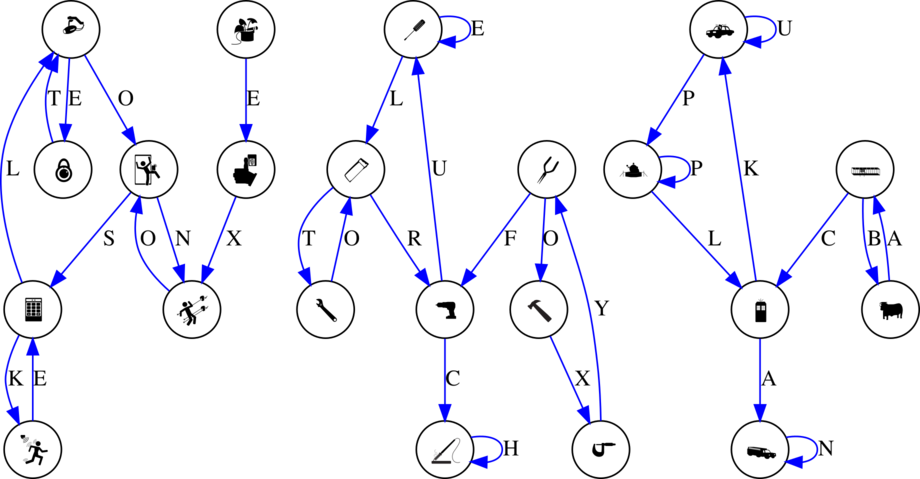
Allowing only these transitions transforms the plans into a maze with a unique solution:

Labelling every transition between icons in the final path spells out the final answer phrase: ON A CALTECH CANNONBALL RUN.