Agricultural Operations (Solution)
by Palmer Mebane, based on an idea by Dan Zaharopol
Take the element that J represents to be a primitive root of the finite field with 25 elements, and let {1, J} be an additive basis of this field. The list below gives the values of each element of the field, listed as
letter: exp, (a, b)
which refers to the value Jexp = a*J + b. Here a and b are elements in ℤ/5ℤ and exp ranges from 0 to 23, or None in the case of the 0 element.
- A: 20, (4, 4)
- B: 15, (4, 1)
- C: 13, (4, 0)
- D: 17, (1, 3)
- E: 6, (0, 3)
- F: 21, (2, 3)
- G: 14, (3, 3)
- H: 10, (3, 1)
- I: 2, (2, 2)
- J: 8, (1, 1)
- K: 12, (0, 4)
- L: 5, (4, 2)
- M: 22, (2, 4)
- N: 19, (2, 0)
- O: 4, (1, 2)
- P: None, (0, 0)
- Q: 16, (4, 3)
- R: 1, (1, 0)
- S: 3, (1, 4)
- T: 9, (3, 2)
- U: 0, (0, 1)
- V: 11, (2, 1)
- W: 7, (3, 0)
- X: 23, (3, 4)
- Y: 18, (0, 2)
The completed grids are shown below:
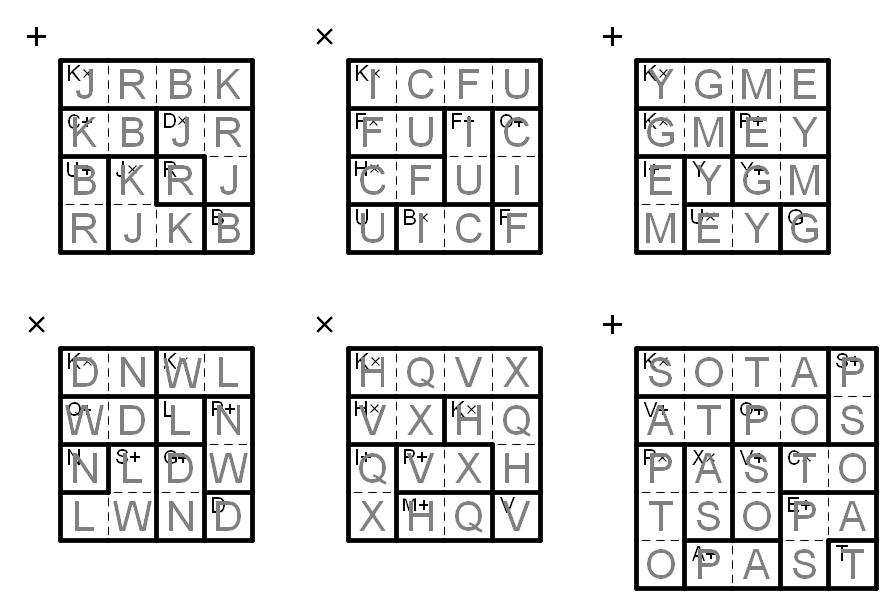
To extract the answer, in each grid take the elements in each upper-left to lower-right diagonal, and perform the operation in the upper-left corner on the grid on them. This gets the following:
E X T A N T
The answer is EXTANT.
 RUBIK
RUBIK