I Left My Stomach In Salt Lake City (Solution)
by Mike Greenberg
Solvers will be presented with a list of linear equations. There are 29 pairs of equations whose graphs meet at points with integer coordinates, and there are precisely 17 distinct such points. Translating these coordinates to addresses in Salt Lake City maps to 6 Japanese restaurants, 3 cafes, 4 Italian restaurants, and 4 McDonald's. Solvers will plot each group of restaurants on a map of Salt Lake City, along with the line segments connecting them (a line segment is mapped if it comes from an equation that contains both restaurant endpoints as solutions). This will spell out one letter for each cuisine (P for Japanese, L for cafes, O for Italian, and T for McDonald's), which gives the answer PLOT (ordering given by flavortext).
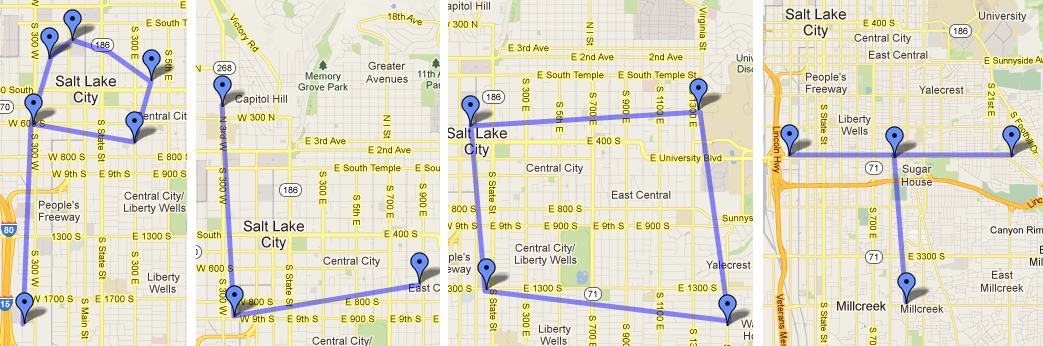
Japanese (P)
| A: Tepanyaki Japanese Steakhouse - 369 W 1830 S | (-369, -1830) | |
| B: Hayai Zushi - 307 W 600 S | (-307, -600) | |
| C: Ginza Japanese Cuisine and Sushi - 209 W 200 S | (-209, -200) | |
| D: Naked Fish - 67 W 100 S | (-67, -100) | |
| E: Ichiban Sushi and Japanese - 336 S 400 E | (400, -336) | |
| F: Koko Kitchen - 702 S 300 E | (300, -702) |
Line Segments: AB, BC, CD, DE, EF, FB
Cafes (L)
| G: Cafe Marmalade - 361 N 300 W | (-300, 361) | |
| H: Jade Cafe - 234 W 900 S | (-234, -900) | |
| I: Tulie Bakery - 863 E 700 S | (863, -700) |
Line Segments: GH, HI
Italian (O)
| K: Big Kahuna Pizza - 38 E 1300 S | (38, -1300) | |
| L: Fresco Italian Cafe - 1513 S 1500 E | (1500, -1513) | |
| M: The Pie Pizzeria - 1320 E 200 S | (1320, -200) | |
| N: Sicilia Pizza Kitchen - 35 W 300 S | (-35, -300) |
Line Segments: KL, LM, MN, NK
McDonald's (T)
| O: McDonald's - 2064 S 300 W | (-300, -2064) | |
| P: McDonald's - 945 E 2100 S | (945, -2100) | |
| Q: McDonald's - 2310 E 2100 S | (2310, -2100) | |
| R: McDonald's - 3890 S 1100 E | (1100, -3890) |
Line Segments: OQ, PR
Original Line Segments (ordered by cuisine)
| AB | (-369, -1830) | (-307, -600) | -615x + 31y = 170205 | |
| BC | (-307, -600) | (-209, -200) | -200x + 49y = 32000 | |
| CD | (-209, -200) | (-67, -100) | 50x - 71y = 3750 | |
| DE | (-67, -100) | (400, -336) | -236x - 467y = 62512 | |
| EF | (400, -336) | (300, -702) | 183x - 50y = 90000 | |
| FB | (300, -702) | (-307, -600) | -102x - 607y = 395514 | |
| GH | (-300, 361) | (-234, -900) | -1261x - 66y = 354474 | |
| HI | (-234, -900) | (863, -700) | 200x - 1097y = 940500 | |
| KL | (38, -1300) | (1500, -1513) | -213x - 1462y = 1892506 | |
| LM | (1500, -1513) | (1320, -200) | 1313x + 180y = 1697160 | |
| MN | (1320, -200) | (-35, -300) | 20x - 271y = 80600 | |
| NK | (-35, -300) | (38, -1300) | -1000x - 73y = 56900 | |
| OQ | (-300, -2064) | (2310, -2100) | -2x - 145y = 299880 | |
| PR | (945, -2100) | (1100, -3890) | 358x + 31y = 273210 | |
| AG* | (-369, -1830) | (-300, 361) | -2191x + 69y = 682209 | |
| IN* | (863, -700) | (-35, -300) | -200x - 449y = 141700 | |
| OD* | (-300, -2064) | (-67, -100) | -1964x + 233y = 108288 | |
| PF* | (945, -2100) | (300, -702) | -466x - 215y = 11130 | |
| QH* | (2310, -2100) | (-234, -900) | -25x -53y = 53550 | |
| RL* | (1100, -3890) | (1500, -1513) | 2377x - 400y = 4170700 |
*Some extra lines were created to make sure that each restaurant was clued in by an intersection of two lines (and are starred above). These lines were made from two points with different cuisines, and since they are not contained within a single cuisine, they do not form parts of letters. This was done so that one couldn't group them into subgroups without identifying the restaurants and cuisines, which would have made it solvable as a pure math problem.