MAN, I HATE THESE %#!&@ SUDOKUS!
by Thomas Snyder
Solution: IN ODD LINES
The initial grids, with less than 17 numbers filled in, cannot be uniquely solved as classic sudoku puzzles. However, once teams receive the instructions, they learn the two properties needed to solve these puzzles: first, no prime numbers ever occur in adjacent cells, and second, no number is repeated in the same cell in any of the puzzles.
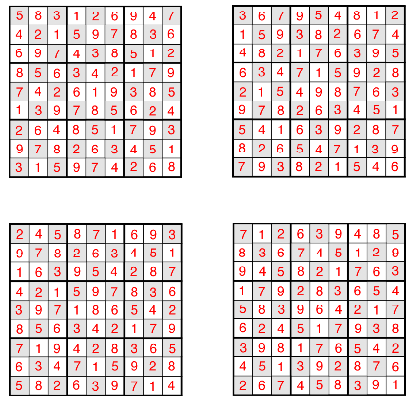
The primes-not-touching constraint requires that 2, 3, 5, and 7 are placed into each box in either a diamond formation, or in four of the five cells that form an X. As each row or column has only four primes, only certain patterns of diamonds and X's are possible. Most boxes, with the exception of the corners, can thus be found to be filled with primes as shown; solving parts of the different puzzles reveals the remaining shaded squares. Once sorting into prime/non-prime is done, the grids become independent challenges involving just primes, and just non-primes, and the no-repeated-numbers-between-puzzles can be used to make headway on either path. The packing of numbers to form valid sudoku is incredibly constrained requiring that all four puzzles are identical with regard to number replacement (so, for example, all the 2's in one puzzle are the same as the 3's in another).
With the sudokus solved, the answer can be derived. The sums of a single cell in all four grids is indicated as the sum of the cell at row X and column Y (RXCY). Adding them together gets:
(R1C5 - R2C5 + R6C5) = 17 - 27 + 19 = 9 = I
2 * (R1C4 - R6C8) = 2 * (24 - 17) = 14 = N
(R9C6 + R6C4 - R3C8) = 22 + 17 - 24 = 15 = O
(R4C7 - R7C2) = 24 - 20 = 4 = D
2 * (R5C8 - R2C2) = 2 * (19 - 17) = 4 = D
(R4C4 - R5C5 + R7C4) = 17 - 24 + 19 = 12 = L
(R1C1 + R3C6 - R5C6) = 17 + 19 - 27 = 9 = I
(R6C1 - R3C2 + R8C6) = 24 - 27 + 17 = 14 = N
(R2C3 - R4C1) = 24 - 19 = 5 = E
(R2C7 + R6C3 - R9C4) = 19 + 27 - 27 = 19 = S
Which, alphanumerically, is IN ODD LINES.
