
Statistics of Lines in Natural Images
(Supplementary material for article)
Natural images are segmented into oriented lines using `steerable filters' (based on the second derivative of a Gaussian and its Hilbert transform)
The following example is taken from M. Sigman et al, PNAS 98, 1935 (2001).

We examined a digital library of natural images, which includes trees, buildings, flowers, leaves, and grass.
(i) Vectors defined in half-planes; averaged over 4 half-planes
 L/T
L/T 
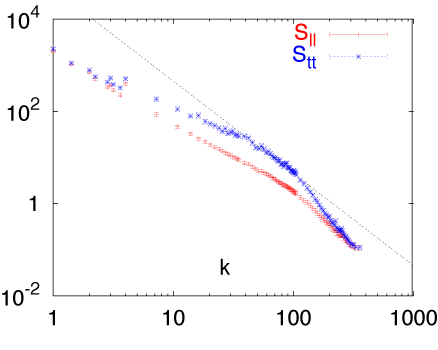
(ii) Vectors and absolute values
For a given k ,
we decompose the orientation field S(x,y) into
components parallel and perpendicular to k ,
and then Fourier transform their absolute value} which are invariant
under S(x,y)=>-S(x,y).
The disadvantage is that mirror image orientations are not distinguished, and
averaging over orientations does not decouple the two components.
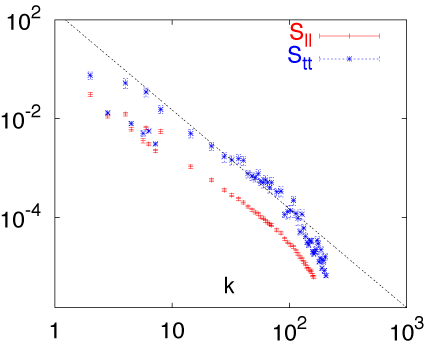
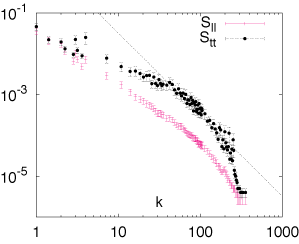
(iii) Tensors (as reported in article)
Convert the orientation field S(x,y) into a tensor S = S • S , and use standard projection operators to project out the transverse and longitudinal components (see article).
 L/T
L/T 
Selected Images from Modern Art