Fitness variations

red ball Individuals in a population carry different mutations which may affect their "fitness."

Can simple models of range expansion shed light on distribution of fitness in a population?

yellow ball Different modes of competition should lead to different fitness distributions (universality classes):      

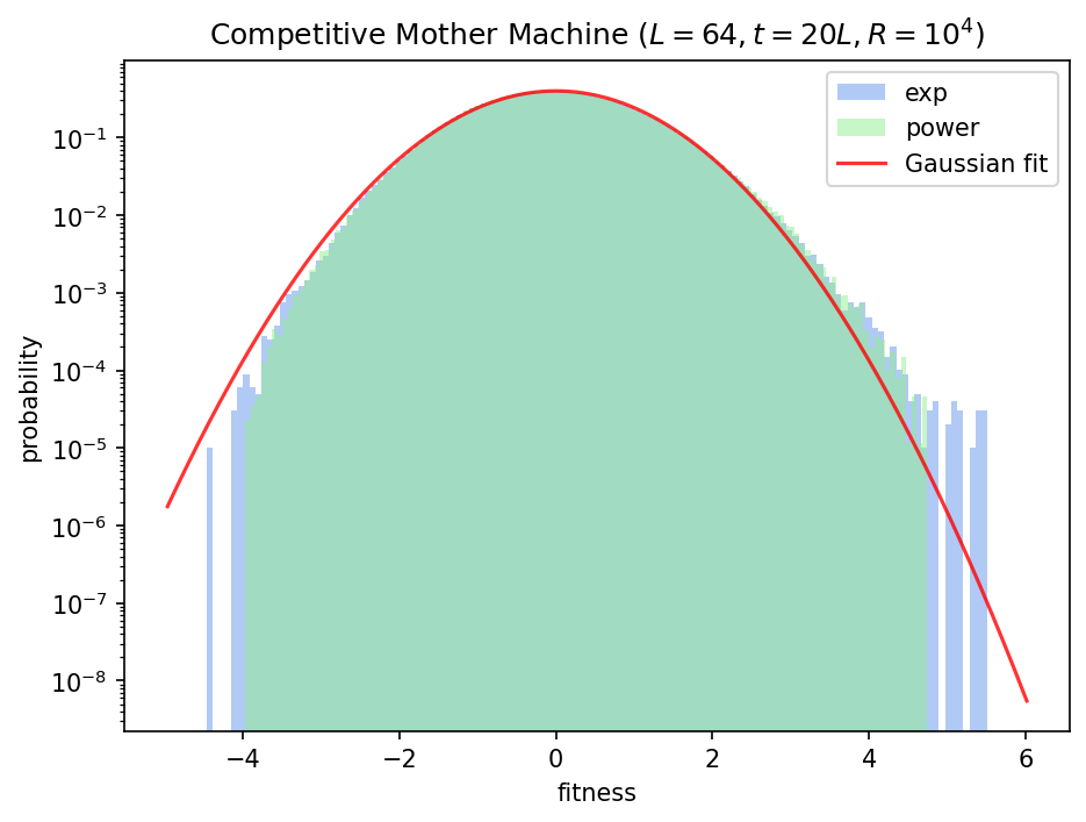
yellow ball "The  Mother Machine" likely provides the simplest case

 

Independent mutations in each column (model, not necessarily reality) should lead to a Gaussian distribution of fitness.

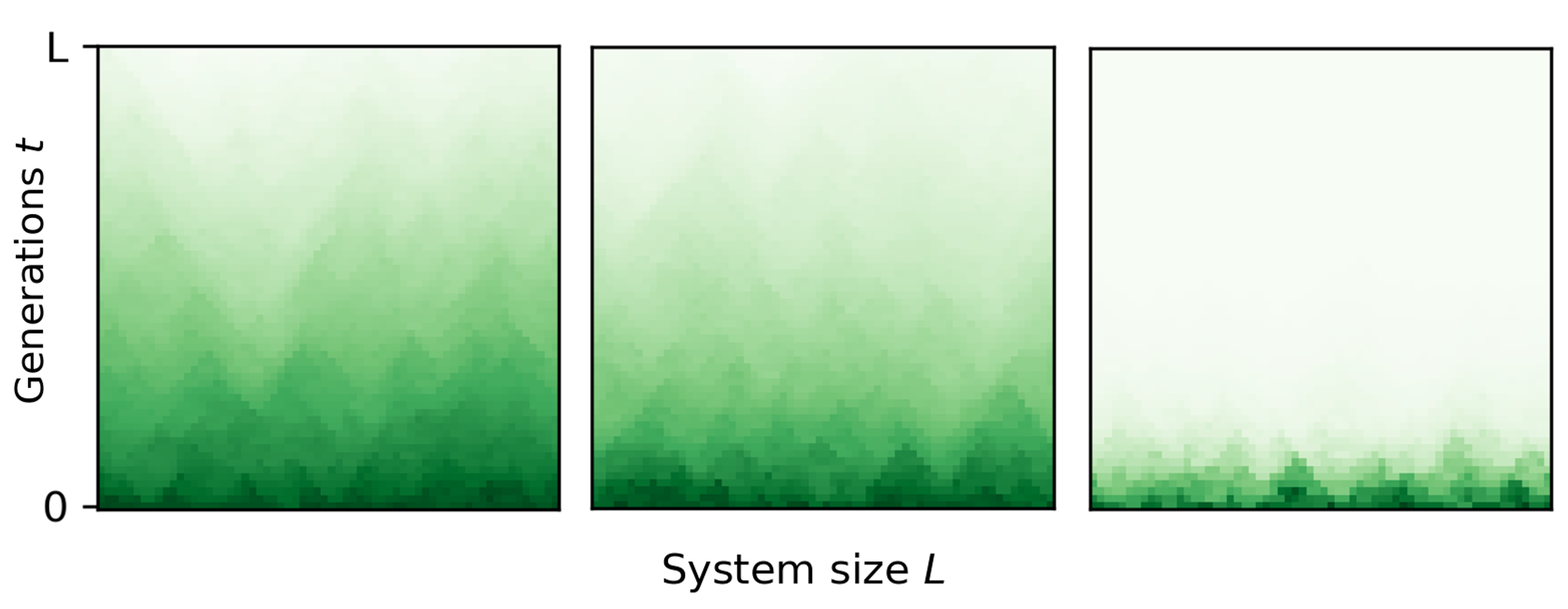
yellow ball By contrast, consider the stepping stone model as competitive (local) range expansion with mutations       

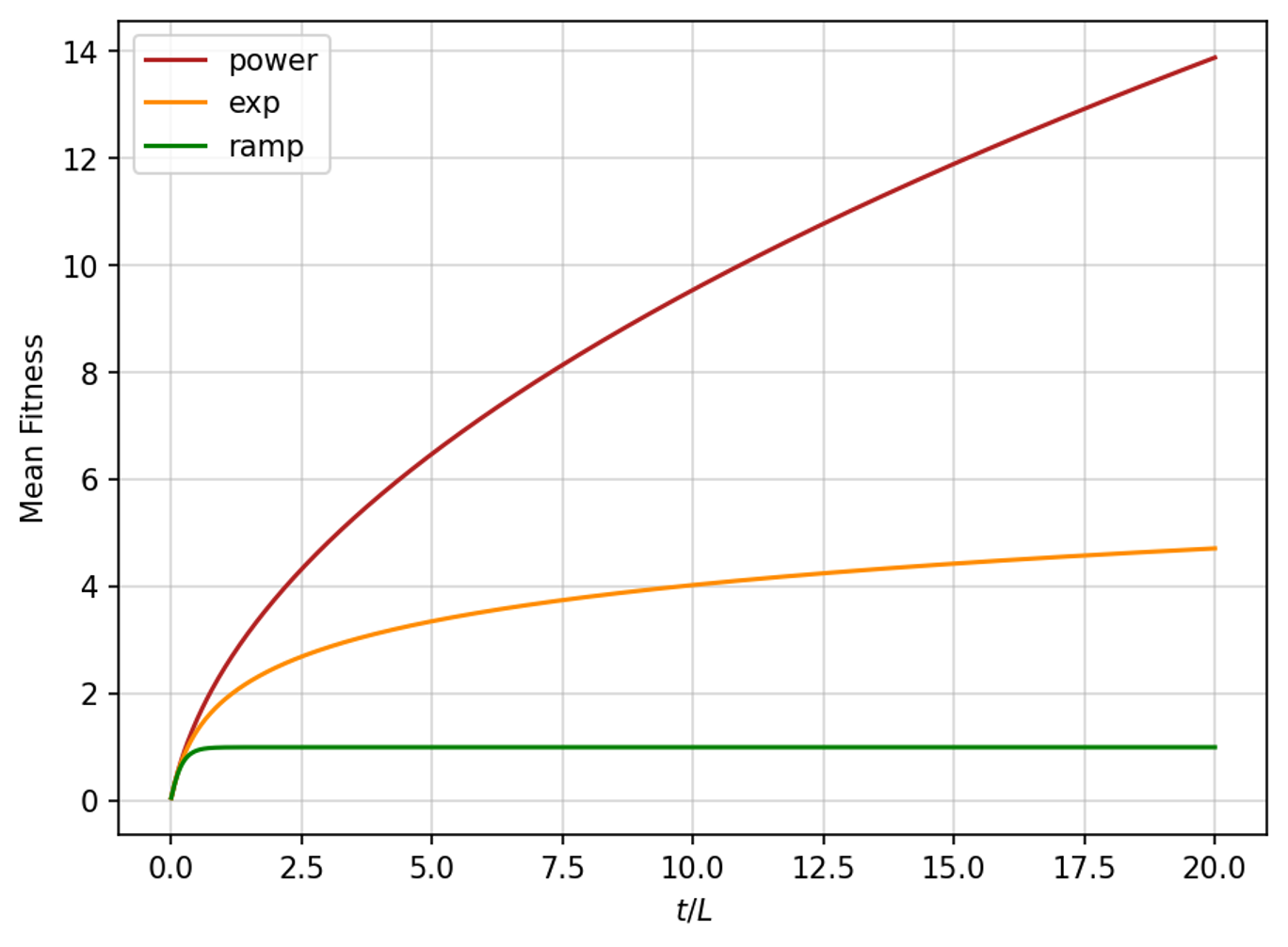
yellow ball By analogy to the "height" of a growing surface, we expect the mean fitness to grow in time,      

 while the fitness distribution follows the (non-Gaussian) skewed Tracy-Widom distribution:       

yellow ball Skewed distributions of fitness could reflect competition on an advancing fitness front.

yellow ball "The Long term evolution experiment"

 

[MJ Wiser, N Ribeck, RE Lenski Long-term dynamics of adaptation in asexual populations. Science 342: 1364 (2013)]

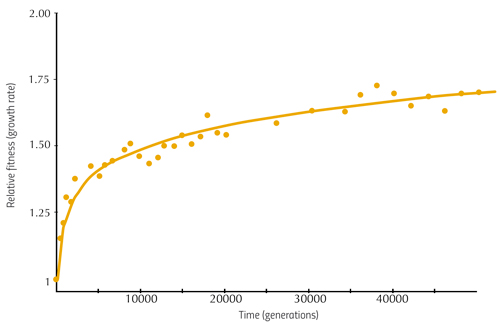
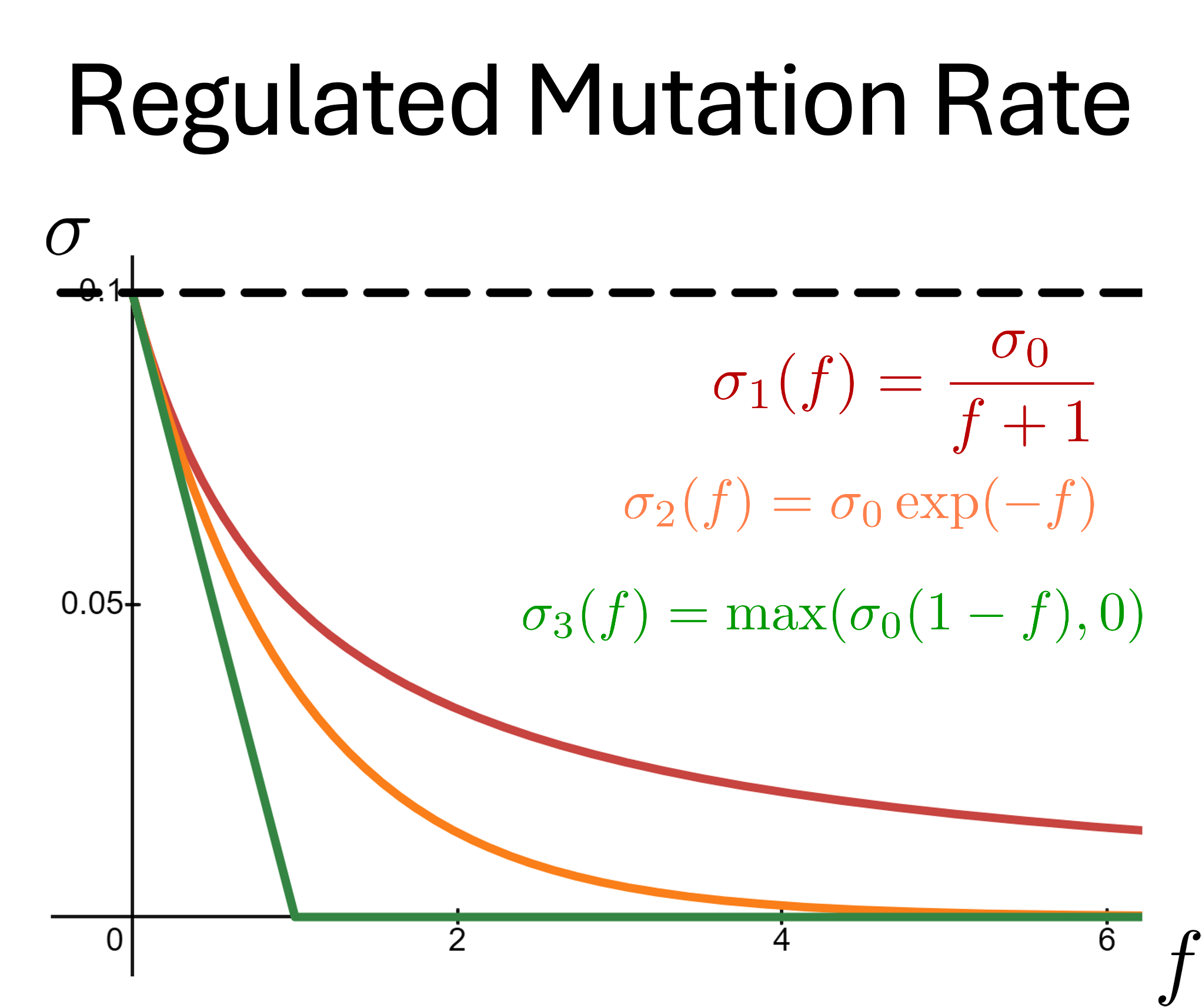
yellow ball An interesting variant that also leads to decreasing growth rate of mean fitness is a mutation rate that decreases with fitness, proposed in

"Regulated somatic hypermutation enhances antibody affinity maturation," Merkenschlager et al, Nature, 641, 495 (2025).