Specialization during Range Expansion
![]() Novel traits evolve to take better advantage of resources, with concomitant changes in fitness
Novel traits evolve to take better advantage of resources, with concomitant changes in fitness
Assume that development of some traits can be indicated by parameter m=b-h ,
such that m=0 corresponds to the ancestor (generalist),
while m>0 corresponds to one trait (e.g.. height), while m<0 corresponds to another
Let us assume for simplicity that the dependence of fitness on m is expressed as a quartic polynomial
![]()
The fitter parent in the stepping stone model wins the competition to reproduce
The child inherits traits from the parent, but also acquires mutational changes
![]()
Starting with generalists ( m=0 ) at t=0 , specialists emerge in time through accumulating beneficial mutations:
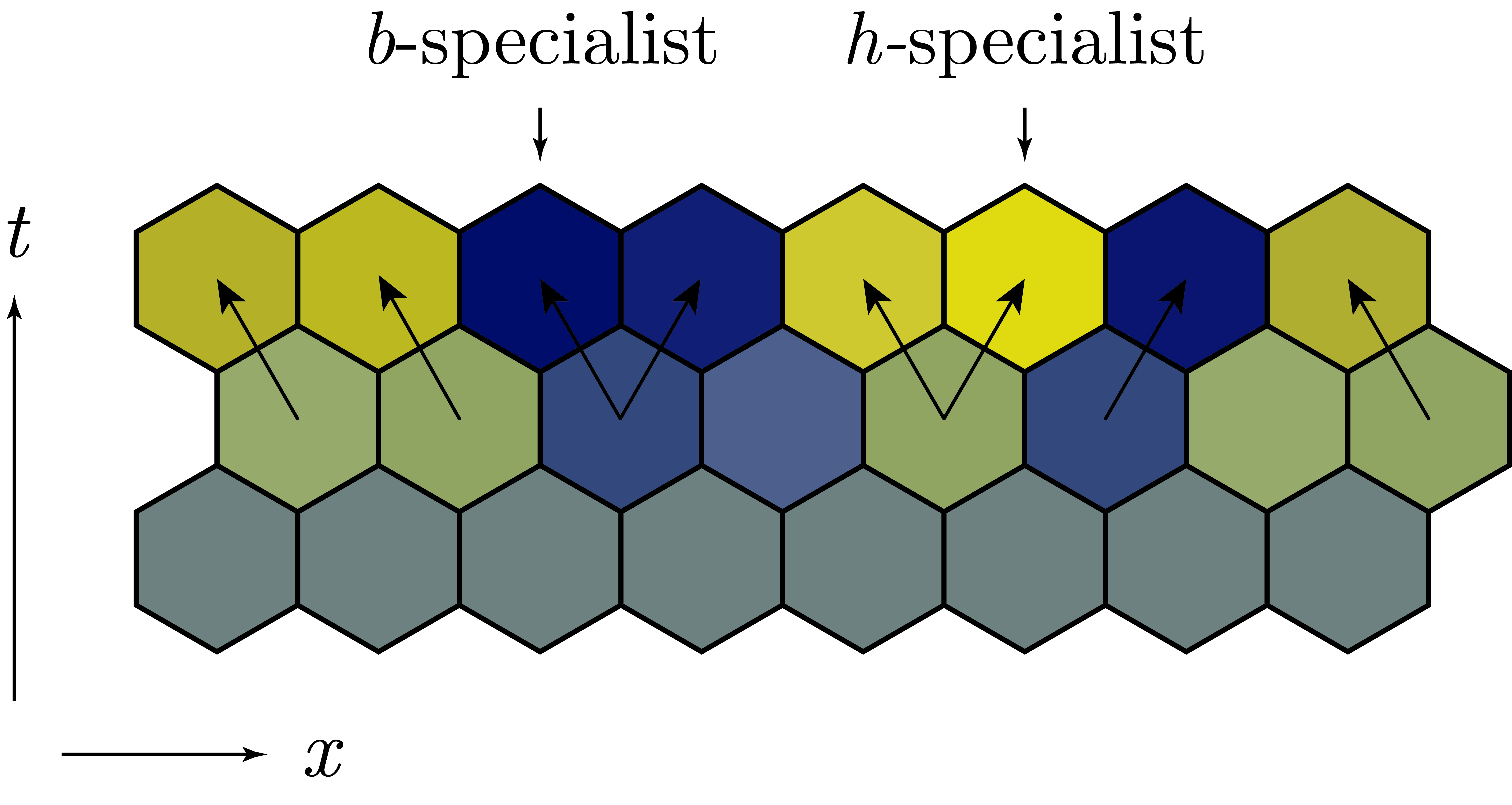
![]() Distinct growth patterns for different fitness functions:
Distinct growth patterns for different fitness functions:
1. Generalists fitness advantage (global)

2. Specialists local fitness disadvantage, but global advantage
3. Specialists fitness advantage (unbounded)
4. Specialists fitness advantage (bounded)
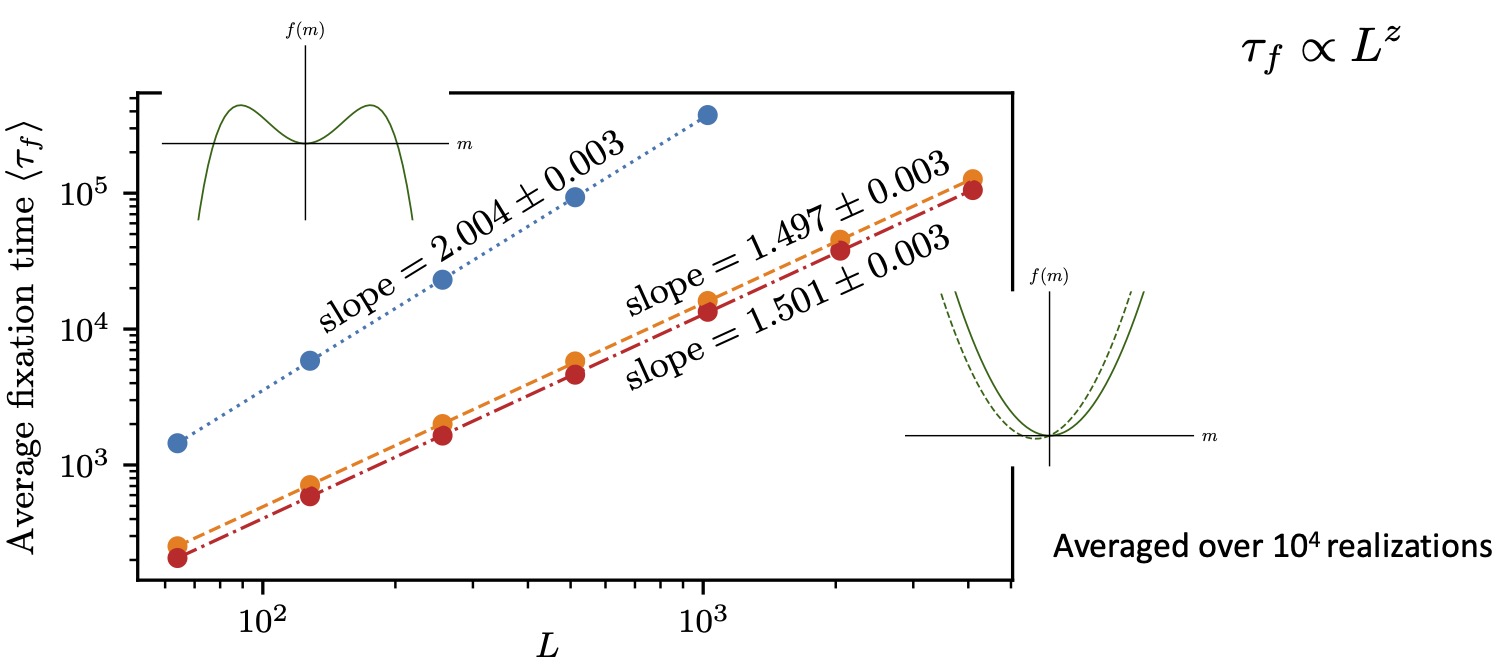
![]() Distinct universality classes for bounded and unbounded fitness gain:
Distinct universality classes for bounded and unbounded fitness gain:
"Specialization at an expanding population,"
Lauren H, Li and M. Kardar, Phys. Rev. E 108, L032402 (2023) (off-line)