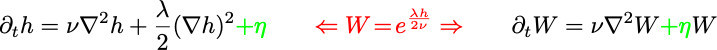
Cole-Hopf mapping
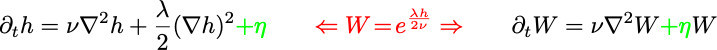
Can we construct such a mapping relating competitive range expansion equations to a solvable model?
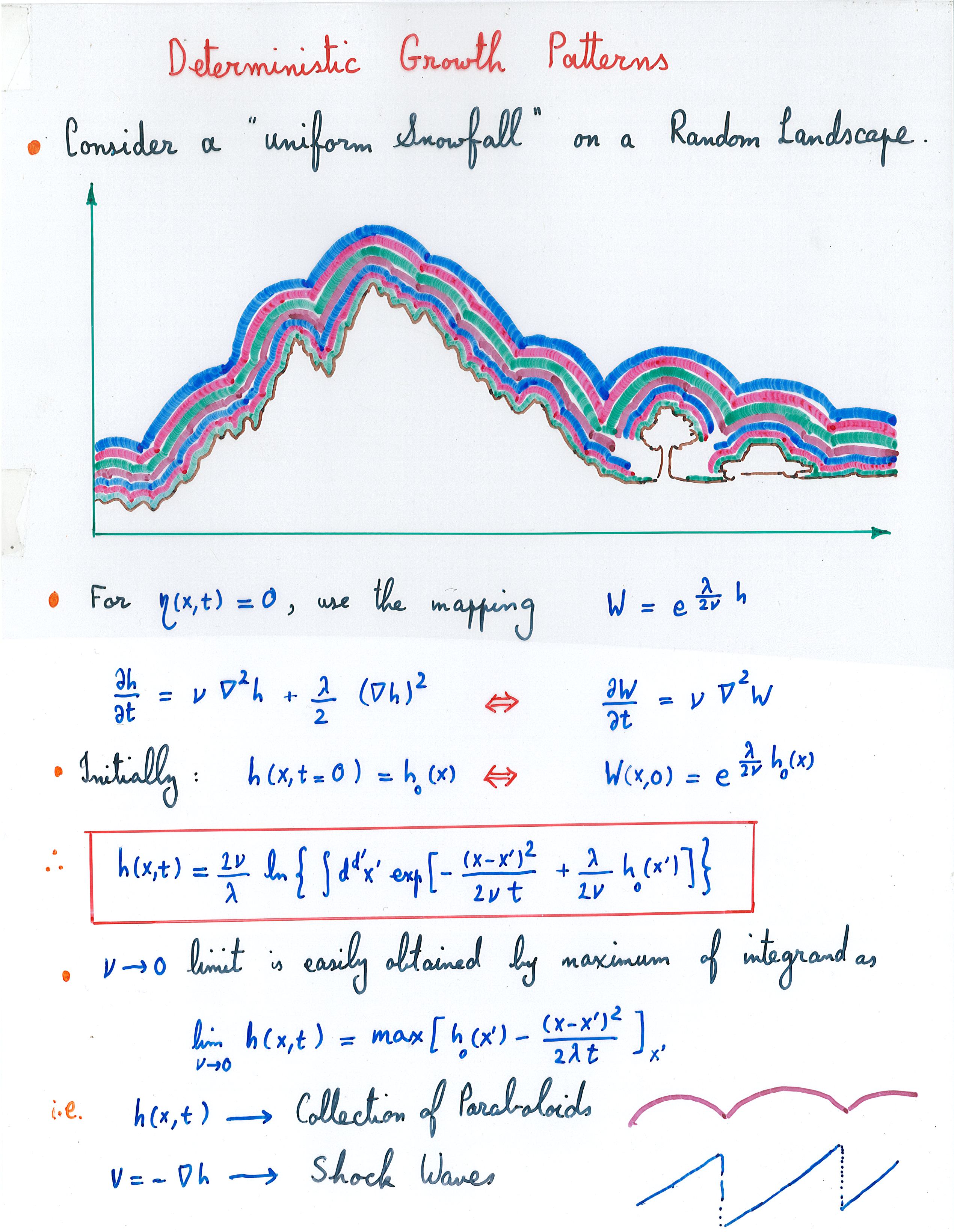
Deterministic (noiseless) limit:
Linear (Eigen's) model of reproduction/mutation of "quasi"-species with added spatial diffusion:
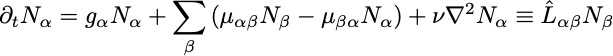
The linear set of equations are in principle exactly solvable:
=_exp(.jpeg)
However, the overall population at each location grows (decays) exponentially in time:
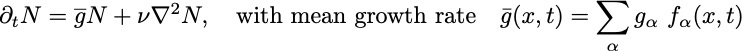
The species fractions at each location evolve as
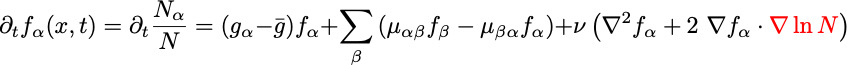
A generalized Cole-Hopf transformation maps this linear problem to a variant of the range expansion model:
=_2_nu_ove.jpeg)
This rough front is now coupled to species fractions according to
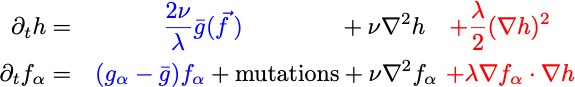
For two species, and no mutations, the corresponding limit of the general coupled equations takes the form:
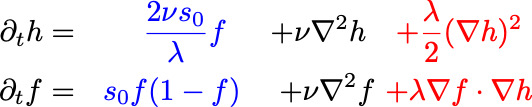
Consequences:
(1) The mapped equations are precisely at the boundary between sloped and circular arc morphologies!
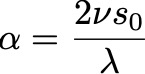
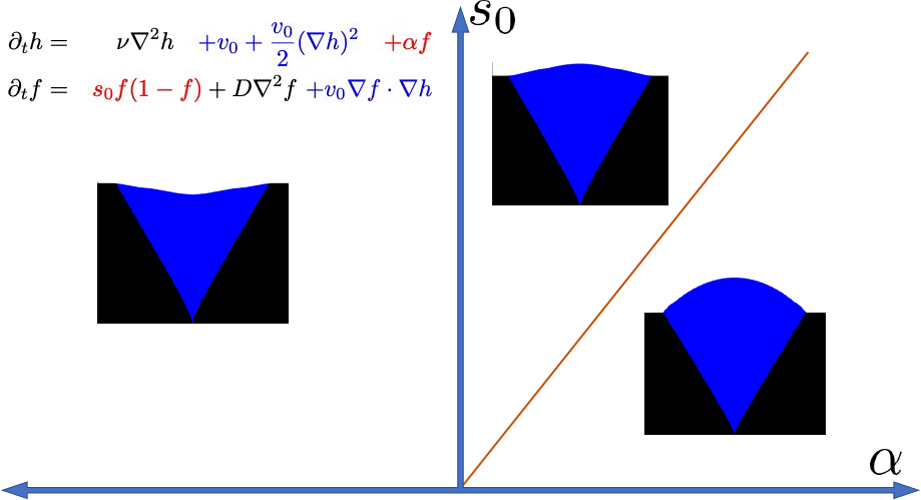
(2) Starting with an initial seeding of species on a rough surface, the deterministic coupled equations can be solved exactly.
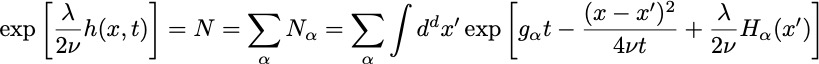
where =_h(x,.jpeg)
The coarsening pattern at longer times can be obtained by a saddle point approximation as
=_1_over_l.jpeg)
A non-flat initial profile grows into a series of coarsening paraboloids:
Each paraboloid is dominated by a single species located at an initial peak.
In the above picture, the blue species is less fit than the gray, and would have gone extinct on a flat front,
the advantage of initial location allows it to carve out its own geographic niche.
In this system the advantage of height h is equivalent to a exponentially larger seed population.
"Bacterial range expansions on a growing front: Roughness, Fixation, and Directed Percolation," J. Horowitz & M. Kardar PRE 99, 042134 (2019) (off-line)
(3) A circular arc invades a flat region with speed approaching the Fisher velocity asymptotically with a Bramson shift:
_sim.jpeg)
Deterministic (noiseless) limit
