Pressure in Equilibrium and Active Matter
Equilibrium pressure: is a function of state, related to confinement of translational entropy
Force per unit area of the wall is a bulk property:
independent of the shape of the container and potentials at the wall
independent of shapes of the particles
independent of the dynamics of the particles (e.g.., partial pressure of colloids)
For a dilute gas: 
(non-universal corrections)
Active matter? Some examples: (Asymmetrically coated colloids, shaken grains, swimming cells, ...)
What is the Pressure of an Active particle fluid? Does it behave like an equilibrium system?
A. P. Solon, J. Stenhammar, R. Wittkowski, M. Kardar, Y. Kafri, M. E. Cates, J. Tailleur, Phys. Rev. Lett. 114, 198301 (2015);
A. P. Solon, Y. Fily, A. Baskaran, M. E. Cates, Y. Kafri, M. Kardar, J. Tailleur, Nature Phys. 11, 673 (2015)
Two common models are Run and Tumble Particles (RTP), and Active Brownian Particles (ABP):
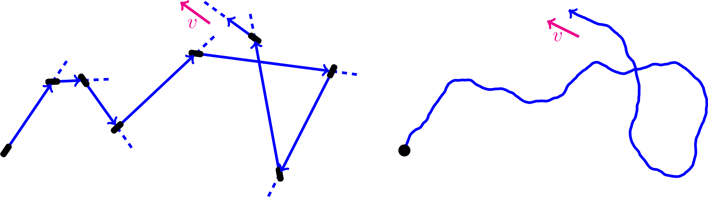
Force and pressure can be measured by introducing a wall potential:
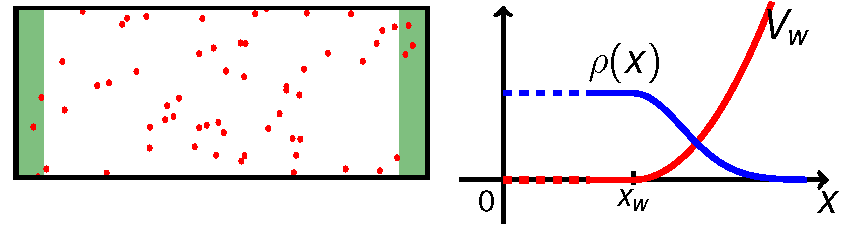
Reorientation of an active particle close to the wall needs to be separately specified:
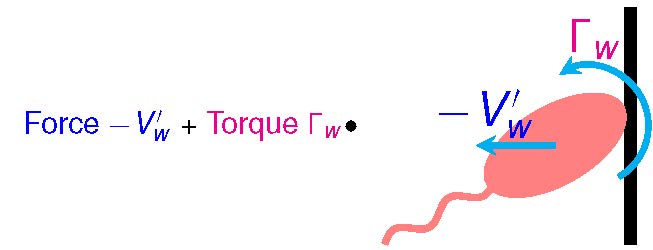
Active pressure depends on the particle shape and reorientation by the wall potential - No equation of state!
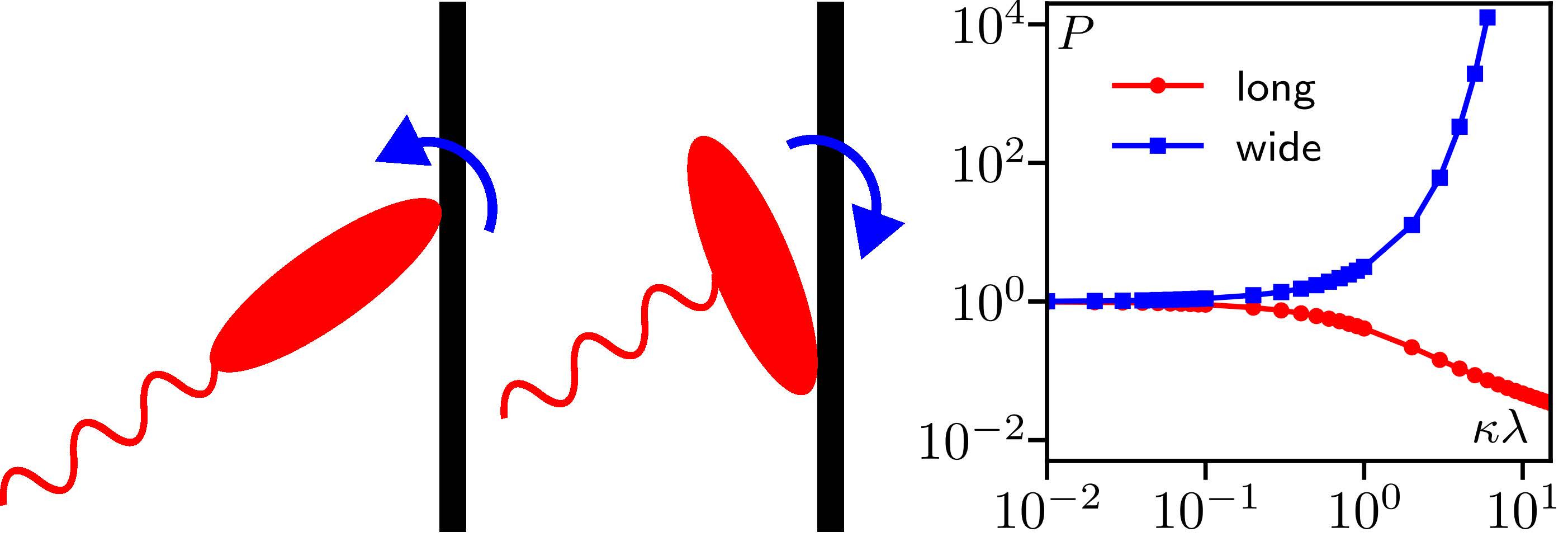
Force on asymmetric wall in homogeneous active gas:
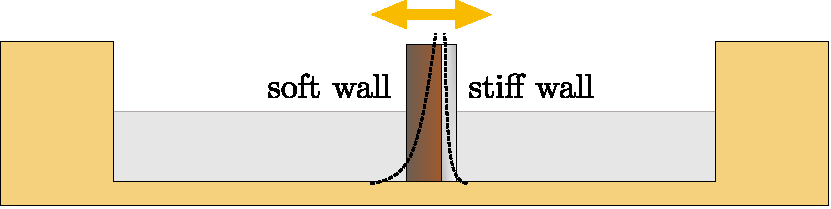
Net force on an isolated box (note the absence of momentum conservation)?
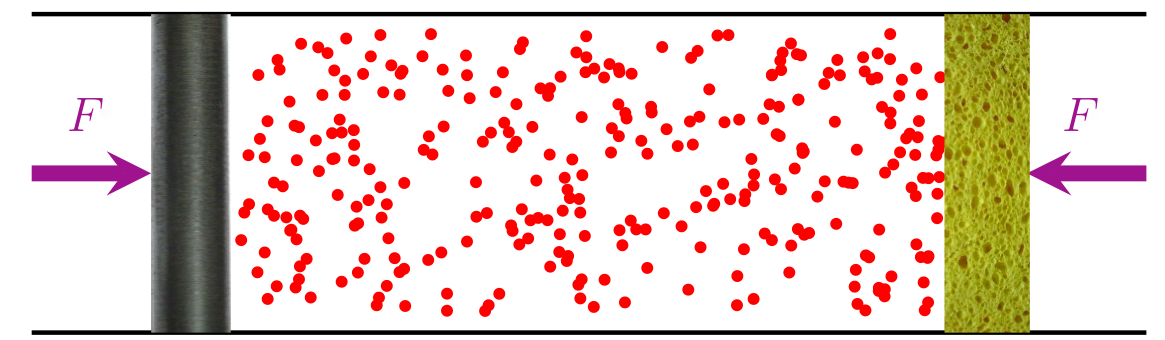vs.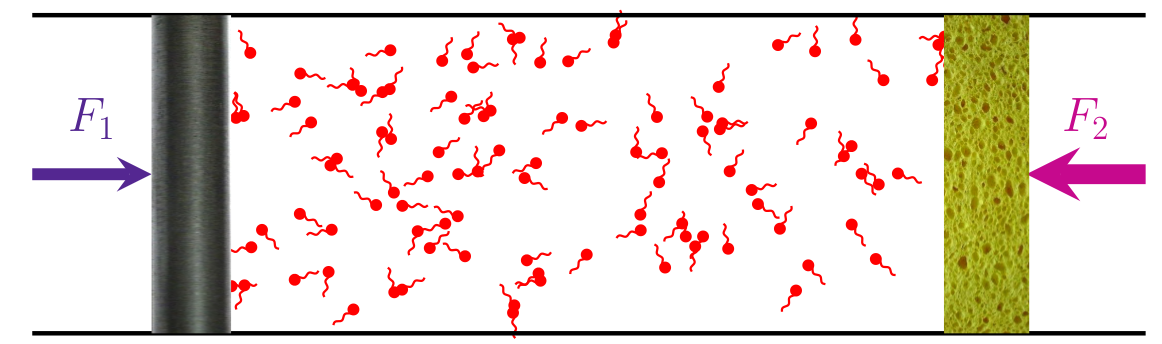
No boundary torque (zero net force) vs. Boundary torque (net force)
In the absence of external torques, a net force is constrained as averaging active particle equations of motion gives:
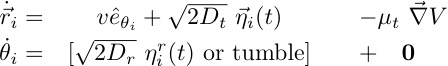
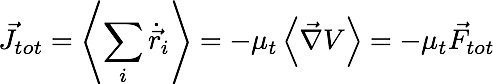
For a closed box the total force and current will both be zero independent of wall potential, suggesting an equation of state.
However, there remain important consequences of activity even in the absence of wall-induced reorientation.
There is a net force on a closed box. (Note that there is no momentum conservation.)
vs.
