Phase separation and disorder

 Interacting active particles (with or without attraction) can undergo

Motility Induced Phase separation (MIPS) M.E. Cates & J. Tailleur, Ann. Rev. Cond. Mat. 6, 219 (2015)

 

Higher densities slow movement; density increases in regions of slow movement instability and phase separation

  What happens to this phase transition if active particles move on a random (short-range correlated, bounded) landscape?

Analogy from equilibrium: What happens to ordered magnets in the presence of (quaenched) random magnetic fields?

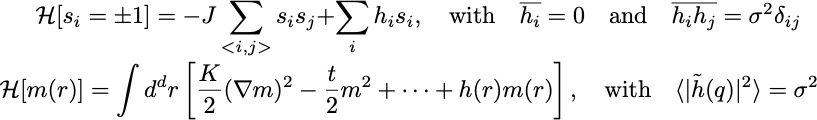
Imry-Ma: Consider stability of an ordered domain of size  R  to flip to the oppositely ordered state;

The ordered phase is unstable to random field induced flips of large enough domains for

  MIPS: For non-interacting active particles, density variations are similar to those expected for an equilibrium system

in response to a spatially varying potential (magnetic field) with long-range correlations:

  Comparison to   

suggests the following analogy to an equilibrium phase separating mixture:

Adapting the Imry-Ma argument to the long-range correlated random fields yields

The (MIPS) ordered phase is unstable to random pump induced flips at large enough scales for

Sunghan Ro, Y. Kafri, M. Kardar, J. Tailleur, Phys. Rev. Lett. 126, 048003 (2021)

The absence of MIPS with disorder is supported by simulations:

Quench with no disorder:

Quench with bulk disorder:

Turning on bulk disorder in a phase separated state:

Turning off bulk disorder:                                     

Next (Boundary disorder) Outline Pressure Boundary shape Inclusions Disorder Phase separation Boundary disorder Summary