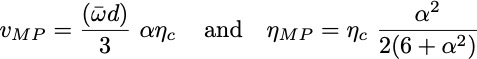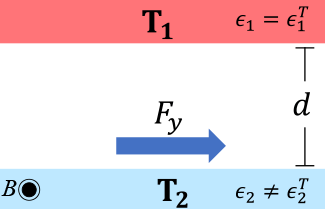
Power and efficiency in the near field

 For simplicity, the results will be expressed in terms of the Carnot efficiency:

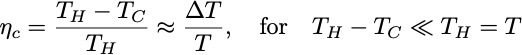
To extract power, the plate must move with some velocity v, leading to efficiency

A naive interpretation of the above formula is that the Carnot efficiency is reached at a velocity scale

Onsager's relations, however, imply that if heat exchange drives motion, motion must modify heat exchange according to

while there are also frictional forces (even with a vacuum gap) reducing the propulsive force to

 Focusing on a single material frequency  , and expressing the degree of non-reciprocity in terms of a single dimensionless parameter   :

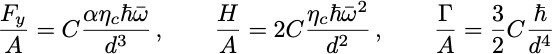
(C is a dimensionless function of  hω/kT  and reflectivities of the two bodies)

This leads to a final expression for the efficiency of

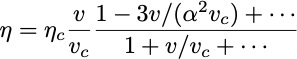
For maximum power

Next (summary) Outline Force Motion Heat Reciprocity Efficiency Summary