Introduction
Hendrik
Brugt Gerhard Casimir (1909-2000)
H.B.G.
Casimir, Proc. K. Ned. Acad. Wet. 51, 793 (1948)
Normal modes
of the Electromagnetic (EM) field between (ideal metal) plates:
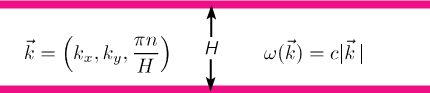
Quantum fluctuations
of these modes, lead to a zero point energy: (see, e.g. Casimir
effect)
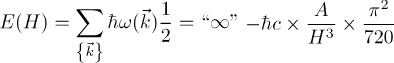
This leads
to a finite attractive force between plates,
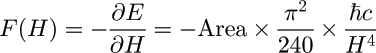
Lifshitz
theory generalizes to parallel plates of arbitrary (frequency
dependent) dielectrics
"The
Theory of Molecular Attractive Forces Between Solids," E.M. Lifshitz, Soviet
Physics 2,
73 (1956)
Experimental Verification
Early experiments
provided at best qualitative support for an attractive force:
M.J.
Sparnaay, Physica 24, 751 (1958). [Aluminum
plates at distances H>1µm]
Abrikosova
& Deriagin, Sov. Phys. JETP 4, 1957 (1957). [Silica
lenses]
van
Blokland & Oveerbeek, J. Chem. Soc. F-T. I 74, 2637
(1978). [H 1-100 nm]
The era of
high precision tests, started with S. K. Lamoreaux 
"Demonstration
of the Casimir Force in the 0.6 to 6µm Range," (using
a torsion pendulum)
Phys. Rev.
Lett. 78, 5 (1997)
U.
Mohideen (and collaborators at UC Riverside), using atomic force
microscopy
"Precision Measurements of
the Casimir Force from 0.1 to 0.9mm,"
U. Mohideen and A. Roy,
Phys. Rev. Lett. 81, (1998)
T. Ederth (geometry
of crossed cylinders)
"Template-stripped gold surfaces
... Casimir force in the 20–100-nm range,"
T. Ederth, Phys. A 62,
062104 (2000)
G.
Bressi, G. Carugno, R. Onofrio, and G. Ruoso,
"Measurement of the Casimir Force
between Parallel Metallic Surfaces,"
Phys. Rev. Lett. 88,
041804 (2002)
R.S. Decca,
D. Lopez, E. Fischbach, and D.E. Krause, Phys.
Rev. Lett. 91, 050402 (2003)
"Measurement of the Casimir Force
between dissimilar metals,"
Applications
F.
Michael Serry, Dirk Walliser, and G. Jordan Maclay,
"The role of the casimir effect
in the static deflection and stiction of membrane strips in microelectromechanical
systems (MEMS),"
J. Appl. Phys. 84,
2501 (1998)
E.
Buks and M. L. Roukes,
"Stiction, adhesion energy, and
the Casimir effect in micromechanical systems,"
Phys. Rev. B 63, 033402
(2001)
H.
B. Chan, V. A. Aksyuk, R. N. Kleiman, D. J. Bishop, Federico Capasso,
"Quantum Mechanical Actuation
of Microelectromechanical Systems by the Casimir Force,"
Science 291,
1941 (2001)
G.
Palasantzas and J. Th. M. De Hosson,
"Pull-in characteristics of electromechanical
switches in the presence of Casimir forces: Influence of self-affine
surface roughness,"
Phys. Rev. B 72, 115426
(2005)
Challenges
Geometry:
non-planar shapes, roughness, ...
Material:
non-ideal metals, impurities, ...
Environment:
finite temperatures, gas particles, ...
