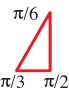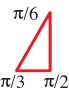ERRATA for The Symmetries of Things
Thanks to the many readers -- including but not limited to Dirk
Frettloeh, Branko Grünbaum, David Eisner, Ward Heilman, Dirk Huylebrouck, Guy
Inchbald, Craig Kaplan, Guyan Robertson, Gordon Williams, Jürgen
Richter-Gebert, Tom Kent, Lewis Stiller, Tony Durham, and Tom Ruen -- who have
taken the time to help us improve our book. Here's hoping that the
third printing will be error free!
Ordered by appearance in the text.
Mathematical notation is presented in the LaTeX typsetting language. The environments \re{} and \bl{} induce red and blue font colors, respectively.
Last updated 5/9/20.
Report unlisted errors to:
hburgiel@gmail.com
Page xv first line: change Besche-Eick-OBrien to Besche-Eick-O'Brien
Page xv seventh bullet point: change Architectonic and Catoptric to Architectonic
Page xvii third line: change Three tracery to Three traceries
Page xvii line 16: change Sienna, Italy to Siena, Italy
Page xviii eighth line from end: change
Birhombohedrille, models and photograph by Chaim Goodman-Strauss.
to
Birhombohedrille, made of Rhombo blocks created by Michael S. Longuet-Higgins. Photograph by C. Goodman-Strauss
Page xviii sixth line from end: change
Pencil hexastix, construction by John H. Conway, photograph by Chaim Goodman-Strauss.
to
Pencil hexastix, model and photo by C. Goodman-Strauss, construction by John Conway and George Hart.
Page 10, in the caption: change Milan Cathedral window (Courtesy of
Valeria Gibertoni and Giovanni Petris) to Milan Cathedral
window
Page 27 first sentence: change wonders, gyrations, kaleidoscopes
and mirrors to wonders, gyrations, kaleidoscopes and
miracles.
Page 36 second line: change *AB...C to *AB...N.
Page 38 last line: change $\re{xx}$, and $\re{*x}$ to $\re{*x}$, and $\re{xx}$
Page 40 incorrect labels on first marginal figure: replace Figures/Chap3/Ch3_S632_triangle with:
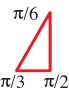
Pages 43, 45, 47, 49: irregular line widths in some of the figures.
Page 52 line 12: change symmetries of this table has to symmetries of this table have
Page 58, Table 4.1:
$\re{*432} = O_h = O x C_2 = S_4 x C_2$ should be in the column marked "P x 2".
$\bl{532} = I = A_5$ should be in the column marked "P".
$\re{*532} = I_h = A_5 x C_2$ should be in the column marked "P x 2".
Page 60, first caption: change This cube has type $\bl{332}$; an
unmarked cube has type $\re{*432}$. to This marked cube has type
$\bl{332}$; an unmarked cube has type $\re{*432}$.
Page 61, second caption: change its type is $\re{2x}$ to its type is $\bl{2}\re{x}$
Page 73, final solution to problem 2: the final frieze has symmetry
group $\bl{2}\re{*\infty}$ if we ignore the flower petals or
$\re{*\infty\infty}$ including flower petals.
Page 81, third to last paragraph. Replace:
We can therefore suppose that $$(V - Nv) - (E - Ne) + (F - Nf) <
cR$$ for some number $c$, and so $$ch = v - e + f < |(V - E + F +
CR / N| < |(2 + cR)/kR^2|.$$ Since the right-hand side of this
inequality tends to zero as $R$ tends to infinity, it must be true
that $ch = 0$.
by:
We can therefore suppose that $$|(V - kR^2v) - (E - kR^2e)
+ (F -kR^2f)| < cR$$ for some constants $c$ and $k$, and so
$$\frac{1}{kR} (-c + (V - E + F)/R) < ch = v - e + f <\frac{1}{kR}
(c + (V - E + F)/R).$$ Since the
bounds of this inequality tend to zero as $R$ tends to
infinity, it must be true that $ch = 0$.
Page 89 line 10: change $V - E + F = 2n - 3n + 2 = 2 - 2n$ to $V - E + F = 2n - 3n + 2 = 2 - n$
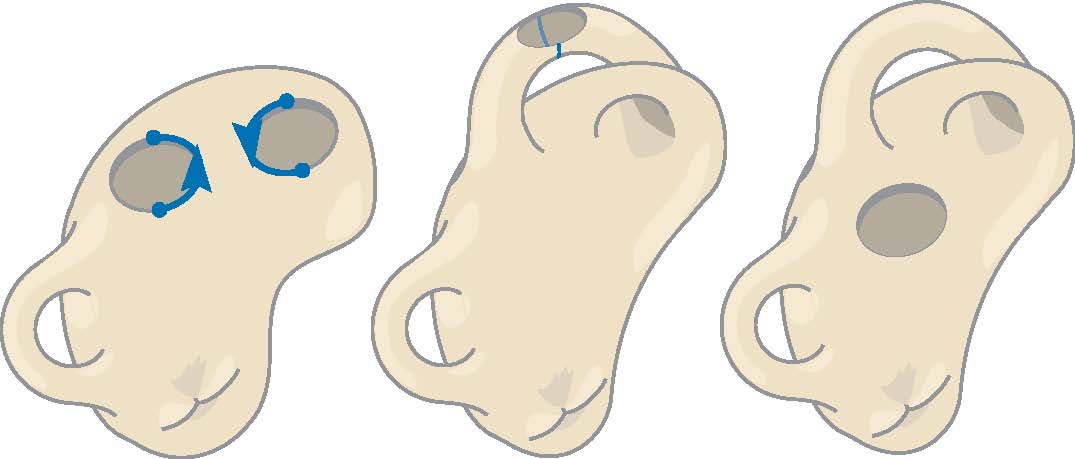
Page 100 Figure 8.8: Second and third images swapped: replace Figures/Chap8/Ch8_gaping_crosshandle with:
Page 102 line 3: change $o x$ can be replaced by $x x$, and so by $x x x$ to $o x$ can be replaced by $x x x$
Page 103 second line from end: change $$2 - 2a - b \mbox{ for } o^a x^b$$ to $$2 - 2a - b \mbox{ for } o^a *^b$$
Page 119 line 1: change The first half of this book to The first part of this book
Pages 120 and 121: remove the duplicate paragraph at the top of page 121; it contains the typo "thisbook"
Page 127 Four lines from the end: 6 3 and 2 should be bold faced:
^\alpha {\bf 6} ^\beta {\bf 3} ^\gamma {\bf 2}
Page 128 first figure: replace Figures/Chap9/Ch9_632_presentation with:

Page 128 third line from end: change = (Q\alpha P\alpha^{-1})^2$$ to = (P\alpha P\alpha^{-1})^2$$
Page 129 fourth line from end: change \alpha \beta \gamma = 1 =
P^2 to \alpha \beta \gamma = 1 = \alpha^2 = \beta^2 = P^2
Page 131 third and fifth lines from end: superscripts alpha and beta
should precede the digits 2: ^\alpha {\bf 2} ^\beta {\bf 2}
Page 136 marginal fig: change A glide reflection interchanging to Glide reflections interchange
Page 136 one line from end: change sometime get technical. to sometimes get technical.
Page 141 line 1: change the "G/H" notation to the "G/K" notation (preserving fonts, etc.)
Page 153 caption: change
(opposite page): Escher's Symmetry Work 70
appears to be three-colored but is actually six-colored! There are
six kinds of butterflies: ... $\bl{632}^3//\bl{333}$.
to
(opposite page): Escher's Symmetry Work 70 is a three-fold coloring of type
$\bl{632}^3/\bl{632}/\bl{333}$ which we abbreviate $\bl{632}//\bl{333}$.
Page 156: In Table 12.1, replace:
\hline
$^\alpha\bl{2}^\beta\bl{2}\re{*}^P$ & $^2\bl{2}^2\bl{2}\re{*}^1\re{2}$ &
\bl{22}\re{*}//\re{**}\\
\hline
with:
\hline
& $^1\bl{2}^1\bl{2}\re{*}^2$ & $\bl{22}\re{*}//\bl{o}$\\
$^\alpha\bl{2}^\beta\bl{2}\re{*}^P$ & $^2\bl{2}^2\bl{2}\re{*}^1$ &
\bl{22}\re{*}//\re{**}\\
\hline
(Adds 22*//o, which is discussed in the next chapter, and removes an extraneous "red 2" from the second column of the 22* row.)
Page 158: The first figure should be replaced by:

Page 162: replace
$^{\alpha}\bl{2}^{\beta}\bl{2}\re{*}^P$ : $\alpha \beta \gamma = 1 =
\alpha^2 = \beta^2 = P^2 = \gamma^{-1} P \gamma
P^{-1}$ Here the two invariant slopes $\infty$ and 0
yield two possibilities; lead to distinct cases: $\alpha \rightarrow
1, \beta \rightarrow 1, P \rightarrow <\!1-t\!>$, which we discard as
intransitive, and $\alpha \rightarrow <\!-t\!>, \beta \rightarrow
<\!1-t\!>, P \rightarrow 1$, or $^2\bl{2}^2\bl{2}\re{*}^1$, type
\bl{22}\re{*}//\re{**}.
with:
$^{\alpha}\bl{2}^{\beta}\bl{2}\re{*}^P$ : $\alpha \beta \gamma = 1 =
\alpha^2 = \beta^2 = P^2 = \gamma^{-1} P \gamma
P^{-1}$ Here the two invariant slopes $\infty$ and 0
yield two possibilities; lead to distinct cases: $\alpha \rightarrow
1, \beta \rightarrow 1, P \rightarrow <\!1-t\!>$, i.e.
$^1\bl{2}^1\bl{2}\re{*}^2$ of type $\bl{22}\re{*}//\bl{o}$, and $\alpha
\rightarrow <\!-t\!>, \beta \rightarrow
<\!1-t\!>, P \rightarrow 1$, or $^2\bl{2}^2\bl{2}\re{*}^1$, type
\bl{22}\re{*}//\re{**}.
(Removes an extra ">" symbol from the second to last line of the text and corrects an error regarding the existence of 22*//o.)
Page 164: replace:
$^\alpha\bl{2}^\beta\bl{2}\re{*}^P$ & $^2\bl{2}^2\bl{2}\re{*}^1$
& $\bl{22}\re{*}^p//\re{**}$ & $p \equiv 1$ (mod 2)\\
with:
$^\alpha\bl{2}^\beta\bl{2}\re{*}^P$ & $^2\bl{2}^2\bl{2}\re{*}^1$
& $\bl{22}\re{*}^p//\re{**}$ & $p \equiv 1$ (mod 2)\\
& $^2 2^2 2^1*^2 $ & $22*^p//o$ & \\
(Adds color symmetry 22*//o.)
Page 170: missing gold arrows; replace Figures/Chap15/Ch15_632_opening_graph with:
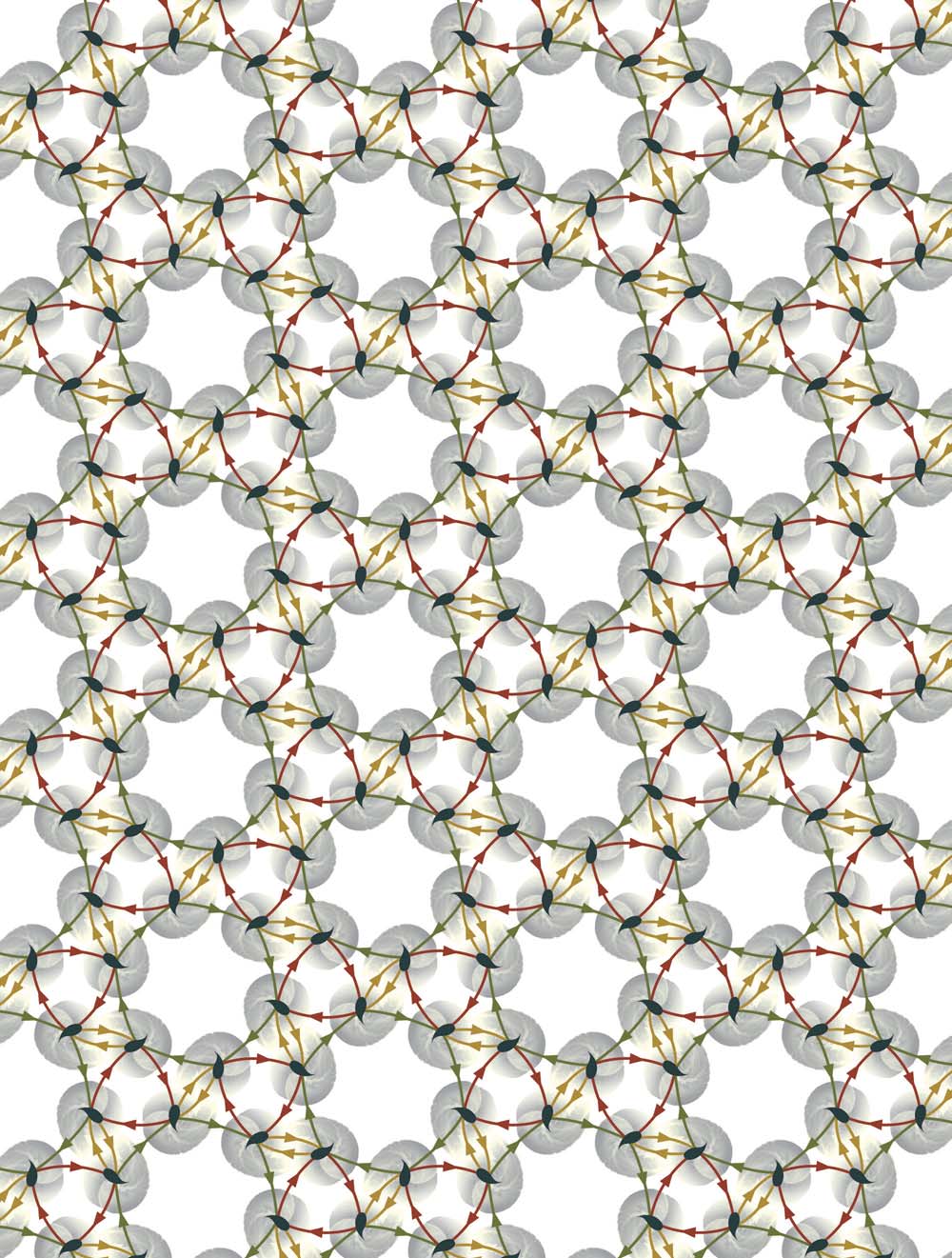
Page 195: one isohedral tiling is missing, one tiling drawn
incorrectly. Replace Figures/Chap16/Ch16_br_heesch_r.eps with:
Page 198 in Row 8 column (Number): change (1) to (5)
Page 200 third line from end: change the {\em Dihedral} group D_n of order to the {\em Dihedral} group D_{2n} of order (preserving fonts, etc.)
Page 217 eleventh line from end: change Kline to Klein
Page 221 sixth line from end: change Figure 17.2 to Figure
17.4
fifth line from end: change perpendicular to the boundary.
to perpendicular to the boundary. (See Figure 17.2.)
Page 224 caption of Figure 17.4: change "Angles and Devils" to "Angels and Devils"
Page 245 caption of Figure 18.5: change Kaleidoscope of $\re{*2243}$ to A kaleidoscope of a non-palindromic signature.
Page 252 third image in illustration: Readers may find it helpful to know that the innermost boundary is brown, the outer boundary is red, and the remaining boundary curve is purple.
Page 261: Errors in table; replace LaTeX code defining table with this code
Page 271 Figure 20.1: change the lower left b to d in
each subfigure.
Page 271 line 6: dimensions 0 and 2 should be dimensions 1
and 2.
Page 274 line 7: change trapeziod to trapezoid
Page 278 line 2: change as "missing groups." to as "missing groups" (i.e. are unfilled).
Page 284 below $"truncated \\ Tetrahedron"$: change tI to tT (preserving fonts, etc.)
Page 285 sidebar: change feminity to femineity
Page 288 line 9: change for an arbitrary polyhedron to for an even-valence polyhedron
Page 293, Table 21.1, second to last line, fourth column: Replace tO
by tT.
Page 298, caption of middle figure, replace tO by tT.
Page 328: change The packing has density $\rho = .9405$, the
unused to The packing has density $\rho = (5 + \sqrt 5)/8 \approx .9045...$,
the unused
Page 324 last line: change they leap to to they lead to
Page 351, replace final paragraph with: The net $[10,3]_a$ was given
its name by A.F. Wells in the 1970s. Its existence is implicit in a
paper written by Laves in the first half of the twentieth century and
it was discussed explicitly by Coxeter in the 1950s. It was
rediscovered as recently as 2007 by Sunada; it is discussed by Ludwig
Danzer in [14].
Page 404 first line of second paragraph: change were discussed already by to were discussed by
Pages 392-400, 402, 403, 411, 412, 413: Schlafli diagrams are missing dots.
Page 410: Remove top left 2-gon and shift the labels à one polygon to
the right.
Page 412: Five lines from the bottom: replace "the interesting Hesse
polytope" by "the interesting Schläfli polytope".
Page 419: remove reference 6.
Page 420 references 18, 19: change Branco to Branko
Page 420 reference 14: change to Ludwig Danzer. Personal
communication, 1996.
Page 426: change runcitruncacted 600-cell to runcitruncated 600-cell