Each part of each problem is worth 5 points out of 100.

1. At National News magazine, 50 reporters won awards last year. Of those 50, 20 had attended a special training program. The magazine employs 200 reporters; out of those 200, 80 attended the training program.

   a) If a reporter is selected at random from among the reporters who attended the special training, what is the probability that that reporter won an award?

    

    

    

    

     b) Are the events "the reporter attended the special training" and "the reporter won an award" independent? For full credit, use the mathematical definition of independence to justify your answer.

    

    

    

    

    

2. The final grades in Professor Burgiel's class is normally distributed (a histogram of the grades has the shape of a bell curve). The average grade is 82 and the standard deviation is 8. What is the probability of a randomly selected student receiving a final grade of over 90?

    

    

    

    

    

    

    

3. After you graduate, you get a job in Boston. As part of your starting package you're offered a choice between a discount rate on parking for a year or subsidized commuter rail tickets for a year. You conside the pros and cons of driving vs. taking the train and decide that you should choose the option for which you spend the least total time commuting.

   The table below shows the commute times in minutes on days with light traffic (these occur with a probability of 80%) and on days with heavy traffic (20%).

   	Light	Heavy
   Commuter Rail	50	50
   Driving	40	100

   a) What choice does the minimax regret decision making approach recommend here? Justify your answer.

   b) What choice does the expected value decision making approach recommend here? Show your work.

    

    

    

    

    

    

    

    

     c) Once you've finished your first year on the job, you'll plan your travel by listening to traffic reports before leaving for work. What is the expected value of perfect information in this situation?

    

    

    

    

    

4. Your new employer is holding a company T-shirt design contest; first prize is free parking for a year. You think designing a T-shirt sounds like a lot of work, but free parking would be nice. Maybe you'll spend some time this weekend figuring out how much money you'd save if you won the contest and switched from riding the train to driving and parking for free.

   a) Draw a decision tree that illustrates all possible sequences of events in this scenario.

   b) Suppose that the cost of designing a T-shirt is $100, the cost of driving and parking for free is $1000, and the cost of taking the commuter rail for a year is $1050. If you don't win the contest you'll continue riding the train; if you do you'll start driving. Assume that you don't know the costs of each option initially but that you can calculate them for free. What is the optimal decision strategy?

    

    

    

    

    

    

5. The Round Tree Manor hotel has two types of rooms (Queen and King) which they rent out in three different packages: economy, deluxe and luxury. The table below shows the profit per night for each type of room and rental package.

   	Economy	Deluxe	Luxury
   Queen	$30	$35	---
   King	$20	$30	$40

   This weekend, Round Tree predicts that there will be demand for 130 economy rooms, 50 deluxe, and 60 luxury rooms. There are 100 Queen type rooms and 150 King type rooms available. They have asked you to use linear programming to determine which rooms to rent at what prices.

   a) This problem can be solved using five decision variables. Decide what decision variables you will use and (carefully!) describe them below.

   b) What is the objective function for this linear programming problem?

    

    

   c) One constraint in this problem is that there are only 100 Queen type rooms available. Write the inequality corresponding to this constraint.

    

    

   d) Write the inequality corresponding to the constraint "there will be demand for 130 economy rooms".

    

    

6. RMC, Inc. manufactures two products: a solvent and a fuel additive. They require three ingredients to produce these products, which we will refer to as Material 1, Material 2 and Material 3. RMC's current stock of these raw materials is limited, so they are operating under the constraints given below; their objective is to maximize their profits.

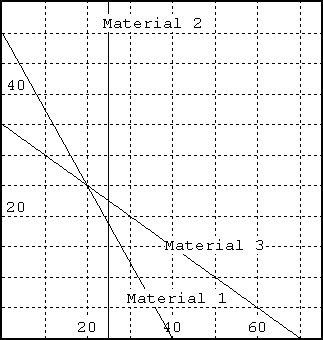
   Maximize:	25S	+	40F
   Subject to:	.5 S	+	.4 F	≤	20	(Material 1)
   	.2 S			≤	5	(Material 2)
   	.3 S	+	.6 F	≤	21	(Material 3)
   			F,S	≥	0

   
   
   Here S represents the number of tons of solvent produced and F represents the number of tons of fuel additive.

   a) Shade in the feasible region for this linear programming problem.

   b) Find the optimal solution.

    

    

    

    

    

    

    

     c) List the binding constraints.

    

    

    

    

    

    

    

     d) Does the optimal solution change if the solvent and fuel base sell for the same price -- for example if the objective function changes to 30S + 30F? Show your work.

7. Shown below is a list of tasks, their dependencies, and their best, most likely and worst case completion times.

   Activity	Dependency	a = best	m = most likely	b = worst	crash cost	Expected
   A	-	2	3	4	50
   B	-	1	2	9	75
   C	A	3	5	7	60
   D	B	2	5	8	100
   E	C,D	4	6	8	80

   a) Compute the expected completion times and enter them in the table above.

   b) Use those completion times to create a project network.

   c) What is the expected completion time of the project?

    

    

   d) Which tasks are critical?

    

    

Bonus: Phyllis is choosing between two investment options. Option A has an 80% chance of yielding a profit of $6000; option B has a 70% chance of yielding a $4500 profit. She knows that if the right conditions are met, option A has a 20% chance to return $7000 while option B has a 30% chance to return $9000. Because of the large sums involved, her financial advisor has recommended that she use the expected utility approach to make this decision. What is the lottery should she use in her utility calculations? (Refer to the end of section 5.2 for more information.)