- Juan has a job through student employment. He must work at least 10 hours a week to pay for his textbooks, but is not permitted to work more than 20 hours a week.
- Megan has asked that Juan spend at least as much time with her as he does on his studies. Juan agrees that this is important.
- Juan needs to spend at least 15 hours a week studying in order to pass his classes.
- Juan also likes to cook and is on an ultimate frisbee team. After spending time on hobbies, sleeping, etc. he estimates that he has 70 hours a week to dedicate to working, studying, and Megan.
a) (10 points) What decision variables will you use? Be clear about what values they hold.
b) (10 points) Write the objective of this linear programming problem in terms of the decision variables.
c) (30 points) Use the decision variables to write the inequalities describing Juan's constraints below.
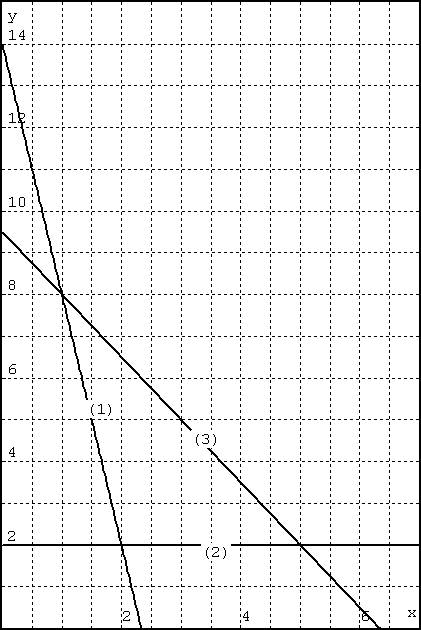
| Maximize: | 4 x | + | 8 y | |||
| Subject to: | 6 x | + | 1 y | ≥ | 14 | (1) |
| 5 y | ≤ | 10 | (2) | |||
| 3 x | + | 2 y | ≤ | 19 | (3) | |
| x | ≥ | 0 | (4) | |||
| y | ≥ | 0 | (5) |
The constraint inequalities for a linear programming problem are shown on the left. The constraint lines are graphed on the right.
a) (15 points) Shade in the feasible region for this linear programming problem.
b) (15 points) Find the optimal solution by plugging the coordinates of the corners of the feasible region into the objective function. Circle the corner corresponding to the optimal solution.
c) (10 points) Which constraints are binding?
d) (10 points) What is the slack associated with constraint number (4)?