MATH100 Sample Final
This is a sample final exam. The questions on the actual final exam
may or may not be similar to these; these questions are similar to
problems that might appear on the final (although sample
problems are often more difficult than those on the final).
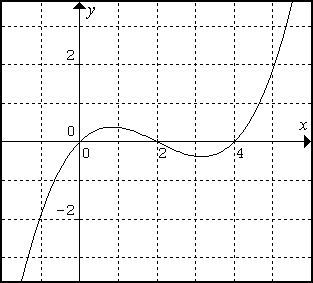
- Shown above is the graph of a function g(x). Use the graph to find approximate solutions to the equation g(x) = 2.
- Shown above is the graph of a function g(x). For what values of x is the function g(x) increasing?
- Give the equation of the line that passes through the point (2,3)
and is perpendicular to the line y = 1/2 x + 1.
- Solve for x: | x - 3 | < 1.
- Sketch the graph of the piecewise defined function:
| f(x) = | x² | 0 < x < 1 |
| x | x > 1 |
- Give the equation of a function whose graph is a parabola that
opens downward from its vertex at (3,4).
- Are the functions f(x) = 2/x and g(x) = 2x inverses of each
other? Justify your answer.
- Give the equation of a third degree polynomial function that has
x-intercepts (0,0), (1,0) and (2,0). You may leave your answer in
factored form.
- Describe all the vertical, horizontal or slant asymptotes of the
graph of the function
h(x) = (x² - 4)/(x² - 2x - 3).
- If log2(x) = 4, what is x?
