Composition of Functions, MATH100
Please work with a partner on this exercise. The purpose of this
worksheet is to read and use graphs of functions in the context of
composition of functions.
Definition: The graph of a function h(x) is the set
of points (x, h(x)).
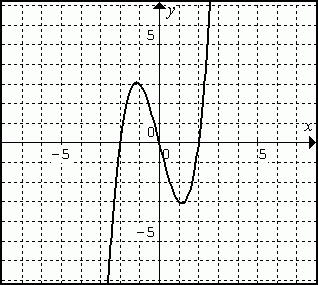Shown above are sketches of the graphs of two functions,
f(x) (left) and g(x) (right). Use the graphs to
answer the questions below. The first question has been done for you.
- Find f(g(-1)).
To find f(g(-1)), we first find g(-1) then
use the graph of f(x) to find f(g(-1)).
- First find find the point in the right hand graph
that is on the x-axis at x = -1.
The graph of g(x) lies above the x-axis at this
point, so trace up from the x-axis to the point
(-1,3) on the graph.
The definition of the graph of a function tells us that this point
on the graph has coordinates (-1, g(-1)), so it must be true
that g(-1) = 3.
- Now find f(g(-1)) = f(3).
In the left side graph of f(x), locate the point on the
x-axis where x = 3.
Trace up from this point to the point (3,4) on the graph
of f(x).
Use the definition of the graph of f(x) to conclude that
f(3) = 4.
- f(g(-1)) = f(3) = 4.
- Find f(g(0)).
- Find g(f(0)).
- Find f(g(-1)).
- Bonus: Use the graphs to find the zeros of the function g(f(x)).