


Next: Eddy Kinetic Energy
Up: Sea Surface Height
Previous: Sea Surface Height Variability
SSH Frequency Spectra were computed at two sample points in the model
domain. In each figure, 3 spectra are shown : 2 spectra from TOPEX at a track
crossover point, and 1 model spectra from daily average output (see
Figs. 18-19). One sample point is near the North Atlantic Current and the other is
very near the Bravo mooring in the convecting region of the interior Labrador
Sea. The model fails generally to have enough energy at most timescales but
especially at high frequencies. It should be noted that the model run used for
comparison here had convective adjustment every 12 hours, not the standard 30
minutes. However, the model fails at high frequencies even outside the
convective region. For this reason, I do not believe that the frequency of the
convective scheme will greatly alleviate the problems in producing high
frequency energy. On the other hand, the model does much better at long
timescales ( 80 days - 1 year) . In the case of the North Atlantic Current
point, the model actually has as much energy as the altimetric
observations. This is a remarkable improvement from previous studies where
model energy is consistently lower than observations at all periods. The long
period variations in this region probably reflect the model's ability to track
the meanders of the North Atlantic Current. By shortening the length of the
timeseries, it was possible to isolate the energy in the seasonal cycle. This
calculation reveals 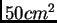 variance or a 30 cm yearly change in sea
surface height around the North Atlantic Current. This is consistent with the
strength of the current. In the case of the interior Labrador Sea, the results
are not as good. Now, model energy is too low at all scales although low
frequencies are more accurate. As reported previously, the model's interior
Labrador Sea does not capture enough total variance of the sea surface. A quick
comparison between the two model spectra shows that the difference in energy
comes from the low frequencies. The interior point has a very flat plateau in
the low frequency region, periods of 50-100 days. Mesoscale eddy variability
can not be directly forced at a point so far removed from the lateral
boundaries. Perhaps, the model's rim current needs to be more baroclinically
unstable or the surface forcing field needs more variability in this frequency
range. To explicitly resolve all eddies in the model, gridpoint separation
should be on the order of 4-5 km. This study suggests that complete resolution
of eddies will have the effect of increasing the variability at all larger
scales even if the variability on the smallest resolvable scales does not
increase dramatically. Although examination of an in-situ spectra is not done
here, it is expected that the total energy at the timescales of convection is
actually small due to the red geophysical spectrum. It is probably more important to
capture the eddies that form as a response to convection if the goal is produce
enough total variability in the model. It is not obvious that adequate
resolution of eddies ensures that their formation may occur from still smaller
unresolvable processes. However, the net result of increasing resolution to 4
kilometers is likely to be very substantial in a wide range of frequencies.
variance or a 30 cm yearly change in sea
surface height around the North Atlantic Current. This is consistent with the
strength of the current. In the case of the interior Labrador Sea, the results
are not as good. Now, model energy is too low at all scales although low
frequencies are more accurate. As reported previously, the model's interior
Labrador Sea does not capture enough total variance of the sea surface. A quick
comparison between the two model spectra shows that the difference in energy
comes from the low frequencies. The interior point has a very flat plateau in
the low frequency region, periods of 50-100 days. Mesoscale eddy variability
can not be directly forced at a point so far removed from the lateral
boundaries. Perhaps, the model's rim current needs to be more baroclinically
unstable or the surface forcing field needs more variability in this frequency
range. To explicitly resolve all eddies in the model, gridpoint separation
should be on the order of 4-5 km. This study suggests that complete resolution
of eddies will have the effect of increasing the variability at all larger
scales even if the variability on the smallest resolvable scales does not
increase dramatically. Although examination of an in-situ spectra is not done
here, it is expected that the total energy at the timescales of convection is
actually small due to the red geophysical spectrum. It is probably more important to
capture the eddies that form as a response to convection if the goal is produce
enough total variability in the model. It is not obvious that adequate
resolution of eddies ensures that their formation may occur from still smaller
unresolvable processes. However, the net result of increasing resolution to 4
kilometers is likely to be very substantial in a wide range of frequencies.



Next: Eddy Kinetic Energy
Up: Sea Surface Height
Previous: Sea Surface Height Variability
Jake Gebbie
2003-04-10