FastAero
Potential flow codes represent an extremely
efficient and accurate means to compute un-separated flow around complex
geometries. The aim of this code project was to develop a code capable of
rapidly solving potential problems around complex geometries in a rapid,
hands-off manner.
FastAero2D
FastAero2D is a two-dimensional potential flow solver
coupled with a simple spring-mass representation of the structural dynamics.
The 2-Dimensional potential flow code exploits and iterative GMRES [6] solver
for rapidly solving the linear system. The potential flow problem is discretized using linear basis functions on flat panels.
Both a thin surface (velocity) formulation and a thick body (Greens Theorem
Thick Body Formulation) have been developed. The unsteady 2-D wake vorticity is represented using a linear element freely convecting, self-influencing wake. As a result the wake
will convect and roll-up under the local velocity
influence (as seen in figure 1).
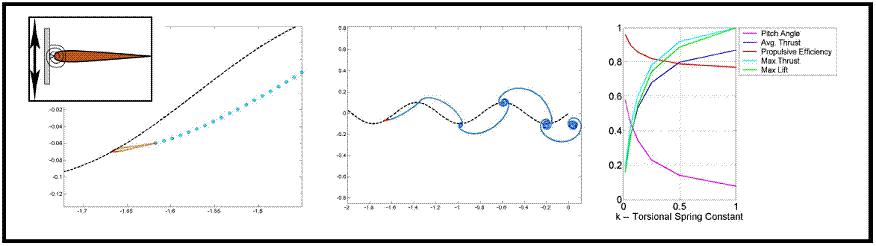
Figure 1: An example of the
2-Dimensional FastAero code applied to a simple heaving wing
motion. In this example the fluid structure interaction is simplified using a leading
edge spring to allow compliance. Although this model is a realistic model of
natural flight, the example lends insight into the effect of leading edge
torsion rod or bone compliance.
FastAero3D
FastAero3D[1] is
an advanced, 3-Dimensional unsteady panel method solver incorporating a large
deformation structural model developed at MIT. The code incorporates an
accelerated iterative solution approach through the use of the precorrected-FFT[3] and Fast Multipole Algorithms[4] (Matrix Vector Product (MVP) acceleration). Through the use of matrix-multiply
accelerations, intermediate time-step solutions can be performed very rapidly.
As such, the solution of highly resolved unsteady potential flows is possible.
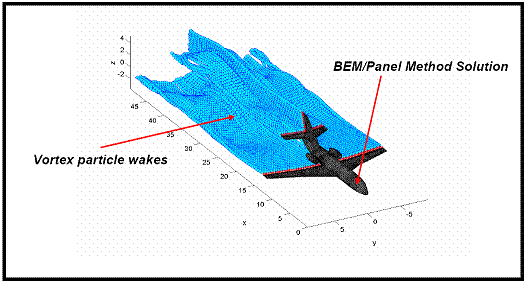
Figure: A plot of the FastAero3D solution around a business jet configuration. In this
image the features of the FastAero3D
solution are illustrated. The body of the business jet is represented using a
boundary element surface triangular discretization.
The localized vorticity in the wake is represented using
the vortex particle method (VPM).
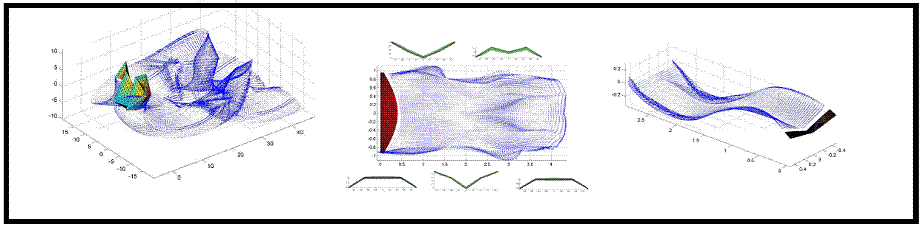
Figure: A plot of the FastAero3D solution around a (left) bat-like model based on
kinematics provided by K.S.Breuer and S.M.Swartz at
EXPORT
DETAILS
The FastAero2D
and FastAero3D codes are both
in-house research codes. The codes were developed by David Willis, Jaime Peraire, Mark Drela
and Jacob White. If you are interested in collaborative
research, or anything further, please contact:
David Willis PhD.
Street:
email: djwillis(at)mit.edu
Jacob White
Street:
email: white(at)mit.edu
ACKNOWLEDGEMENTS
The authors of FastAero
would like to thank:
Junghoon Lee
Carlos Cohelo
Jaydeep Bardhan
REFERENCES
[1]
Willis, D.J., Peraire, J. White, J.K., A combined pFFT-multipole tree code, unsteady panel method with vortex
particle wakes, 43rd AIAA Aerospace Sciences Meeting and Exhibit, AIAA
2005-0854, Reno, NV, Jan. 2005.
[2] Willis, D.J., Peraire, J. White, J.K., 'A quadratic basis
function, quadratic geometry, high order panel method'
presented at 44th AIAA Aerospace Sciences Meeting, AIAA-2006-1253,
[3]
Philips, J.R., White, J.K., A Precorrected-FFT
Method for Capacitance Extraction of Complicated 3-D Structures, Proc. of the
IEEE/ACM International Conference on Computer-Aided Design, pp. 268-271,
November 1994.
[4]
Greengard, L., Rokhlin, V. A
Fast Algorithm for Particle Simulations, J. Comput. Phys. 73, 325 (1987).
[5] Rehbach,
C. Calcul numerique d’ecoulement tridimensionels instationaires avec nappes tourbillonnaires, La Recherche
Aerospatiale, pp. 289-298, 1977.
[6] Saad, Y. and Schultz, M. H. 1986. GMRES: a
generalized minimal residual algorithm for solving nonsymmetric
linear systems.