| |
| Home Bat Flight Flapper Design Tool Development Future Projects Publications Contact the Team |
| HallOpt |
HallOpt is a simple yet powerful tool for determining the first order properties of efficient biologically inspired flight and swimming. The tool is used to determine how an efficient flapping wing locomotive system should generate the unsteady forces during the flapping cycle. HallOpt is based on the wake only analysis approach presented by Hall et al [1][2][3]. It is particularly well suited to flapping flight analysis due to the wake only nature of the model. The geometric details of the wings and the body during flapping are not needed at this low fidelity stage, which significantly simplifies the analysis procedure. The HallOpt method can be used in both 2-Dimensions and 3-Dimensions. The HallOpt approach follows the steps below which are also presented in
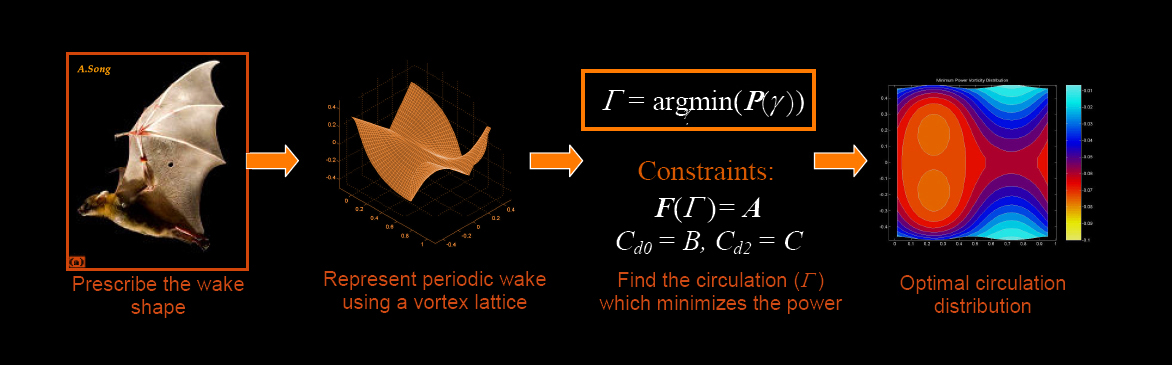
figure 1:
2.
The unknown wake vorticity/circulation
distribution is assumed to lie on this approximate wake surface and is
approximated using a streamwise periodic vortex
lattice.
3.
The unknown wake vorticity/circulation
distribution is determined by minimizing the induced power subject to lift,
drag and side force constraints.
4.
The resulting vorticity/circulation
distribution represents the minimum power wake for that particular flapping
configuration.
Figure 1: An
illustration of the HallOpt process. From left to right, we can see (1) the bat
generates a vortex wake from the lifting surfaces during the flight
motions. In (2) this vortex wake is
represented using a vortex lattice method. The vorticity in the wake can be directly related to the induced power and forces generated
by the flying animal. From the expressions the minimum power wake can be
computed.
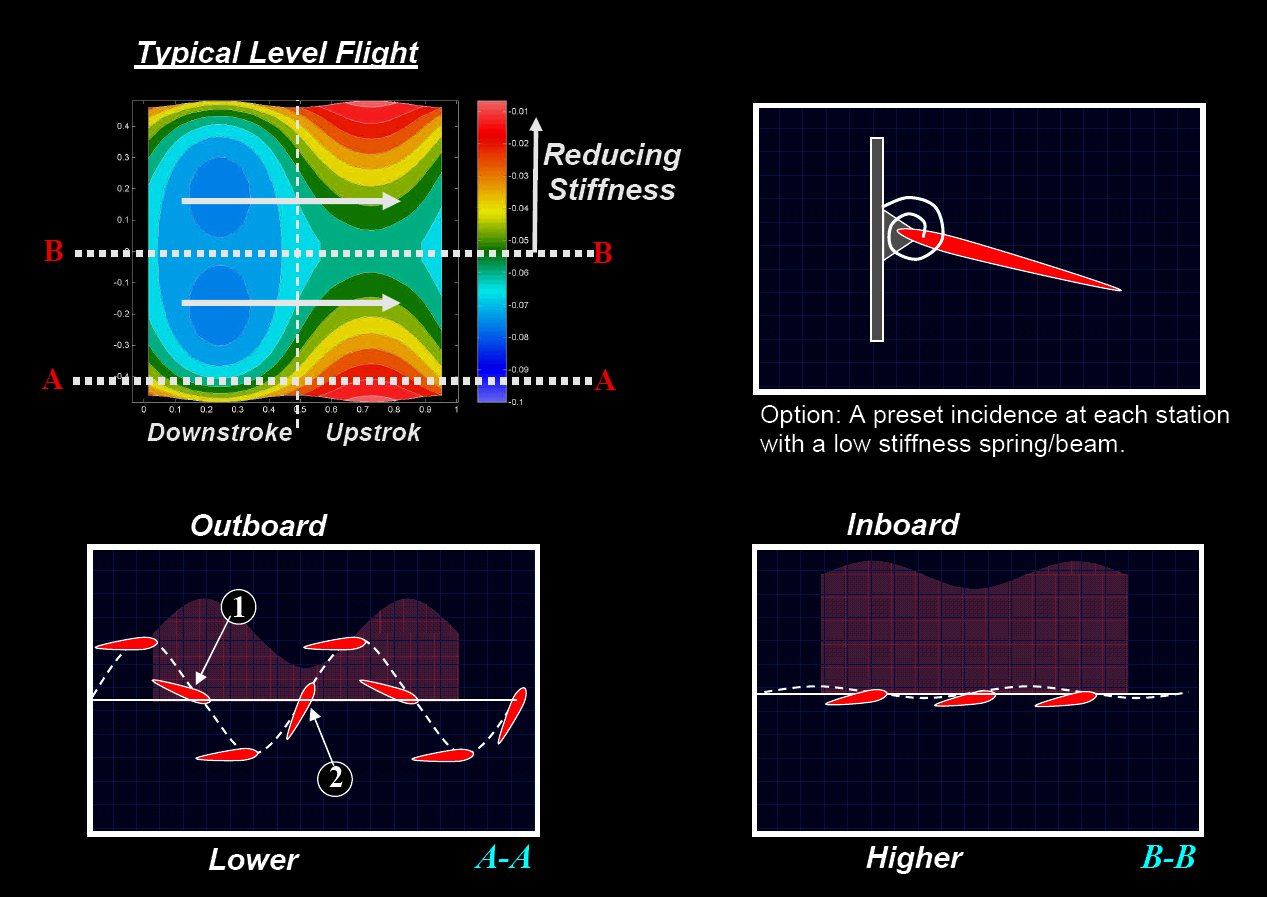
Understanding The HallOpt Wake The wake in Figure 2 is
an illustration of a particular solution of the minimum power wake using HallOpt. In this
image, a top down view of the wake surface trailing the bird is assumed. The
flight direction is from left to right, starting with a downstroke. In order to understand this wake, we examine the
circulation and vorticity distribution. Consider the
wake in the upper-left figure below. The shades of color represent the wake
circulation (blue being larger circulation, red being reduced circulation). The
constant contours of the circulation in the wake represent the vorticity or vortex filaments. As can be seen, there is a
large shed circulation in the wake during the downstroke (thereby producing lift and positive thrust), while the upstroke shows the
alleviation of the loading in the wingtip regions. The upstroke here is active,
and as a result the vorticity distribution exhibits a
ladder like structure for this particular kinematics and lift/thrust
requirement.
The remaining figures
illustrate how this wake might be generated by a simple rigid wing with a
leading edge torsion spring. By observing this required pitching motion, one
can see that a passive structural behavior can likely generate much of the
optimal wake vorticity leaving the fine tuning to be
done by active wing adjustments.
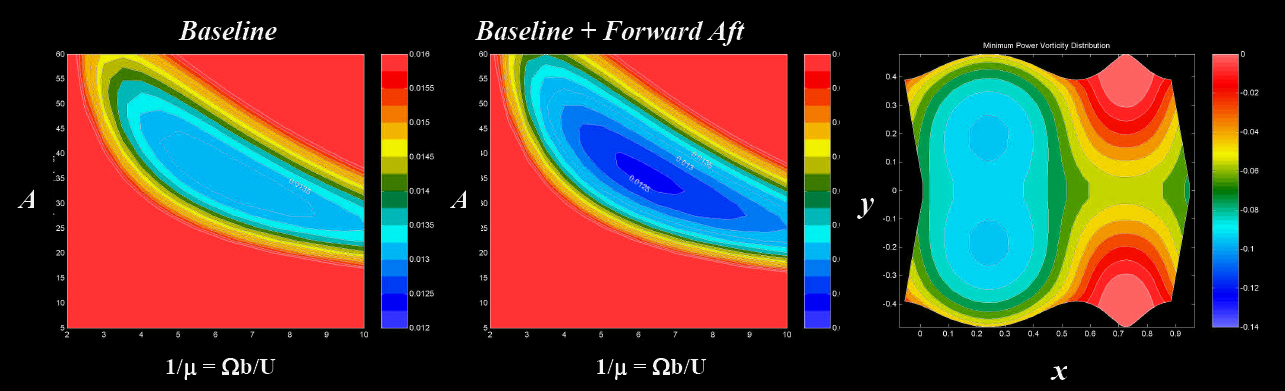
Figure 2: In this figure we present an illustration of the design of a flapping vehicle based on a optimal 3-D wake profile. We have also used the HallOpt code to examine parametric motions parameters.
These studies can be found in [9]. In the figure below, we show the incorporation
of a forward-aft degree of flapping freedom in addition to the baseline up-down
flapping motions. As can be seen, there is an effective reduction in power
consumption due to the presence of the additional degree of freedom. In effect
the forward aft motions in this case allow the wake to have a larger downstroke area and therefore a larger momentum disk from
which to extract forces.
Figure 4: A plot of the amplitude vs. non-dimensional frequency
for a baseline (up-down) motion (left), a baseline + forward aft motions
(middle), and a plot of the resulting optimal wake for this particular
simulation (right).
References
Hall,
K.C., Piggott, S.A., Hall, S.R., Power Requirements for Large Amplitude
Flapping Flight, Journal of Aircraft, Vol 35, #
3, 1998.
Hall, K. C., and Pigott, S. A., "Power Requirements for
Large-Amplitude Flapping Flight," AIAA Paper 97-0827, Presented at
the 35th Aerospace Sciences Meeting and Exhibit,
Hall,
and K.C Hall, S.R., Minimum induced power requirements for flapping
flight, J. Fluid Mech. Vol. 323, pp 285-315, 1996.
Trefftz Plane (Ilan Kroo, Desktop Aeronautics, Info. at, http://www.desktopaero.com/appliedaero/potential3d/InducedDrag.html)
Betz,
A. Schraubenpropeller mit geringstem Energieverlust, Vier Abhandlungen zur Hydrodynamik und Aerodynamik, pp. 68-92, 1927.
Graham K. Taylor, Robert L. Nudds, Adrian L. R. Thomas, Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency, Nature 425,
707–711, October 16, 2003.
Triantafyllou,
M.S., Triantafyllou, G.S. and Gopalkrishnan, R. (1991). Wake mechanics for thrust
generation in oscillating foils. Phys. Fluids A. 3, 2835-37.
Triantafyllou,
G.S., Triantafyllou, M.S. and Grosenbaugh, M.A.. (1993).
Optimal thrust development in oscillating foils with application to fish
propulsion. J. Fluids Struct. 7, 205-24.
D.J.WILLIS, J.PERAIRE, M.DRELA,
and J.K.WHITE, 'A numerical
exploration of parameter dependence in power optimal flapping flight',
presented at AIAA Conference, AIAA 2006-2994,
The current project has been funded by several different sources at different times. We are very thankful to the following funding sources: Singapore-MIT Alliance (SMA), National Science Foundation (NSF), Natural Science and Engineering Councile of Canada (NSERC), and the Air Force Office of Scientific Research.
|
Copyright 2007, MIT. All rights reserved.
Aerospace Computational Design Laboratory, Department of Aeronautics and Astronuatics. Massachusetts Institute of Technology.
| Sample Simulations | ||
|
||