Diffraction Theory Illustrated
Jonathan R. Birge
MIT Ultrafast Optics and Quantum Electronics Group
Overview
In this Mathematica notebook, I illustrate the various approximations used in diffraction theory by focusing on the phase of the impulse responses (Green's functions) implicit in each. I show that Fraunhofer diffraction can be computed using the Fourier transform simply by arguing their equivalence from an impulse response standpoint. I also demonstrate the Fraunhofer diffraction approximation is actually completely conceptually separate from Fresnel diffraction and that it makes little sense to use the Fresnel kernel as is typically shown in books. This will probably only be of much interest to people already briefly familiar with diffraction theory, though the pictures should serve as a nice illustration of what's going on with the approximations for somebody just learning diffraction theory.
Common Functions
These functions will plot the phase fronts of a wave on a normalized set of axes or numberically compute diffraction given a kernel function and aperture function (in 2D). All functions are normalized an assume a wavelength of unity. (These functions are for learning, not actual work!)

Spherical (Exact) Kernel
In scalar diffraction theory, the starting point is usually Huygen's principle, which states that the field emanating from an infinitely small point (i.e. the impulse response in 3D) is a spherical wave. This is needlessly vague and without rigor. Starting from the full vector Maxwell equations, it is common to derive two fundamental wave solutions. The first is the usual plane wave that we're all familiar with. But when talking about computational diffraction these are not useful solutions, because it's difficult to match finite boundary conditions using waves with infinite extent. The other commonly derived solution to the wave equation is a spherical wave emanating from a point dipole. This spherical wave is not uniform in amplitude, and in addition has a polarization (vector) aligned with the dipole. However, the amplitude is fairly uniform we typically don’t deal with polarization in Fourier optics. The transition to scalar diffraction is made by asserting that if the aperture from which we're diffracting is large, the effects of the boundary conditions at the edge of the aperture will be small and won't differ with the polarization of the field." This, then, is the basis behind Huygen's principle. By considering all the points in the aperture as sources of spherical waves, you're doing the same thing electrical engineers do when they solve for the impulse response of a system and convolve it with a driving signal. The spherical solution to the scalar wave equation is the impulse response (green's function) and the aperture is the driving function.
The phase of the impulse response is simply proportional to the distance from the slit (which we'll always assume to be at the origin). In the following plots, we'll just look at the phase, and we'll ignore the fact that the intensity also drops off in proportion to the distance in 2D. (This makes the plots easier to see, and all the interesting features of diffraction are described by the phase.)
![]()
![]()
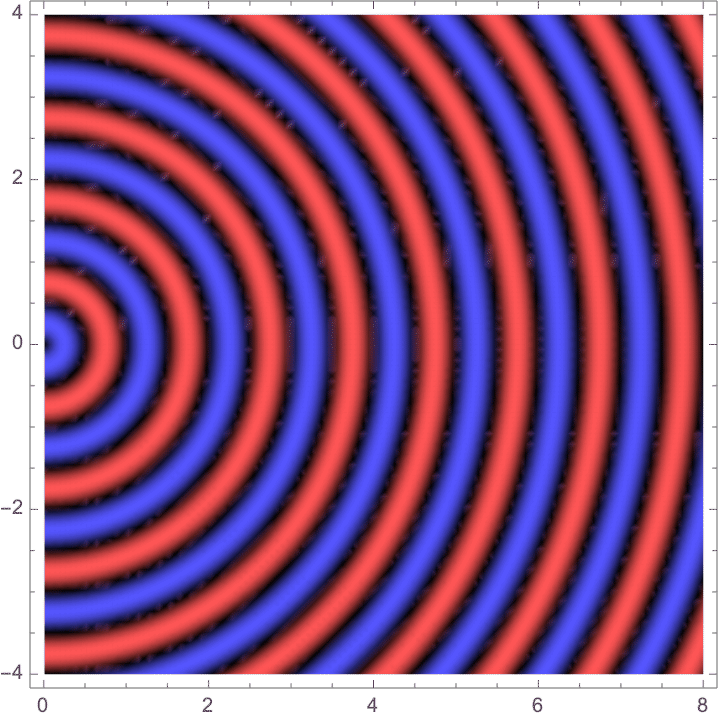
This is actually fine for computational diffraction, especially in two-dimensions (as shown here). The diffraction pattern of an arbitrary aperture can be approximated very quickly and yet accurately by computing the numerical approximation of the spatial convolution of the above kernel with the aperture. However, the radical makes anything but trivial situations impossible to compute analytically, as the integral that results from convolving the spherical wave with the aperture is usually unsolvable.
Given that we can easily compute diffraction patterns with spherical waves, it's fair to ask why people go past this and on to Fresnel and Fraunhofer diffraction. The answer is partly historical and partly conceptual. They certainly didn’t have computers back when these theories were developed. But I will say this, however, because your professors won’t: Fresnel diffraction is completely useless. Fraunhofer diffraction is highly useful, however, since the notion of a Fourier Transform is so powerful.
Fresnel Kernel
Fresnel diffraction theory treats the spherical curvature to second-order along x, eliminating the radical:
![]()
![]()
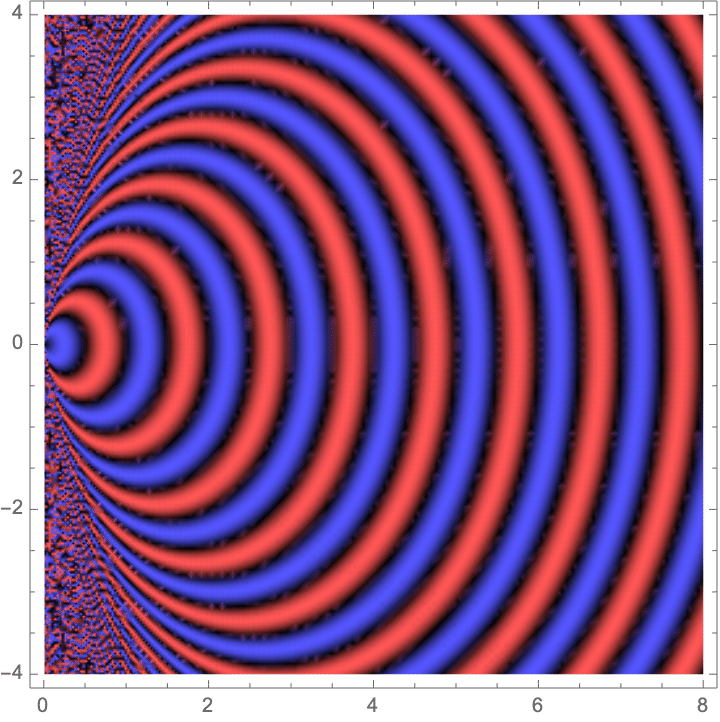
As you'd expect from a Taylor expansion, the approximation gets pretty bad away from the z-axis. It's valid as long as we're within a cone where the ratio of z to x is at least roughly the wavelength. As long as this requirement is satisfied, the result is valid regardless of the distance from the source. For this reason, Fresnel diffraction is also called "near-field" diffraction. (Of course, it's also valid arbitrarily far away, too.) The only problem is that it's still difficult to obtain analytic results for anything but completely contrived cases. Even a knife-edge can't be computed analytically. (Hence the so-called Fresnel function, which--as with all transcendental functions--is just mathematicians' way of saying we can't actually do the integral but would love to sound smart and get rid of the integral symbol.)
What's the point?
It's simply historical and pedagogical. There are really no practical problems that can be solved analytically using Fresnel diffraction. And computationally, it's pretty much as difficult as using the more accurate spherical kernel. Thus, if you're going to use a computer to compute the near-field diffraction pattern you might as well use a spherical kernel.
Fraunhofer (Fourier) Diffraction
Fraunhofer Kernel Shifting
Why is computing the diffraction pattern of arbitrary apertures with Fresnel diffraction difficult? The answer is that the resulting convolution integral is usually unsolvable in closed form, despite the simple form of the kernel. Apparently, it's just not simple enough of an impulse response to be of much use. (Just try yourself to compute the diffraction pattern from something as simple as a square function aperture.) Fortunately, there is another approximation that can be made if we assume that we are far enough from the source such that the source “seems small” in the sense that we never have to consider the kernel very far off axis during convolution.
Far away from the origin, small lateral shifts of the impulse response can be approximated by simply multiplying the kernel by an appropriate pure linear phase. That this is valid can be shown mathematically, and it can be intuitively argued from the point of view that the wave fronts a small distance from the z-axis are "tilted" an amount that is linearly proportional to the distance. This is simply the notion of a series expansion applied to the wavefront. So, the Fraunhofer approximation not only requires that we are in a region of large radius of curvature of the wave fronts, but also one where the aperture appears "small" so that we needn't consider the kernel very far off the x-axis. This latter requirement is why Fraunhofer diffraction is also called "far-field" diffraction since we must be far enough away for the source to be negligible in extent.
The amount of linear phase we need to add is proportional to the shift, Δx, as well as the slope to the location in the diffraction plane. For a unit displacement in our current normalized units, we have:
![]()
![]()
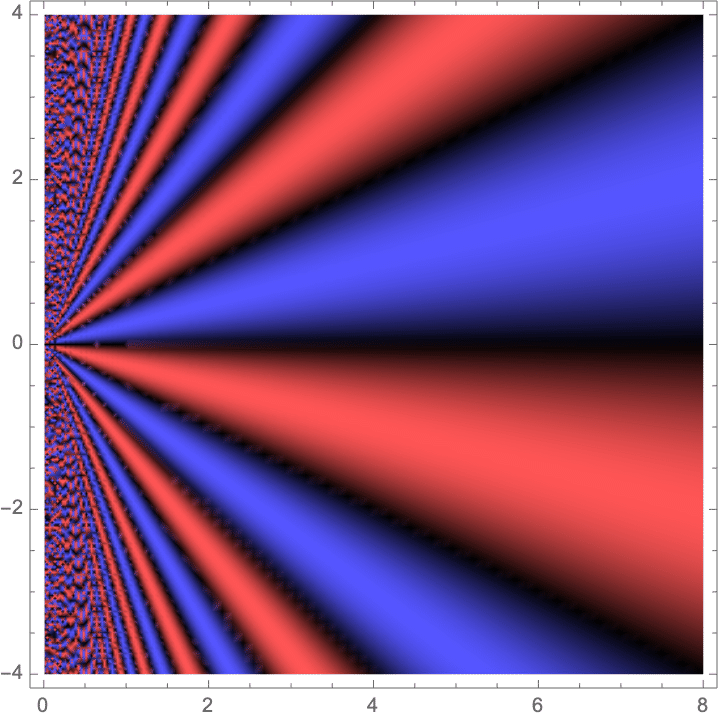
If we add this phase to an unshifted Fresnel kernel, we should get something that looks just like the Fresnel kernel (at least far away from the source) but shifted down by one unit:
![]()
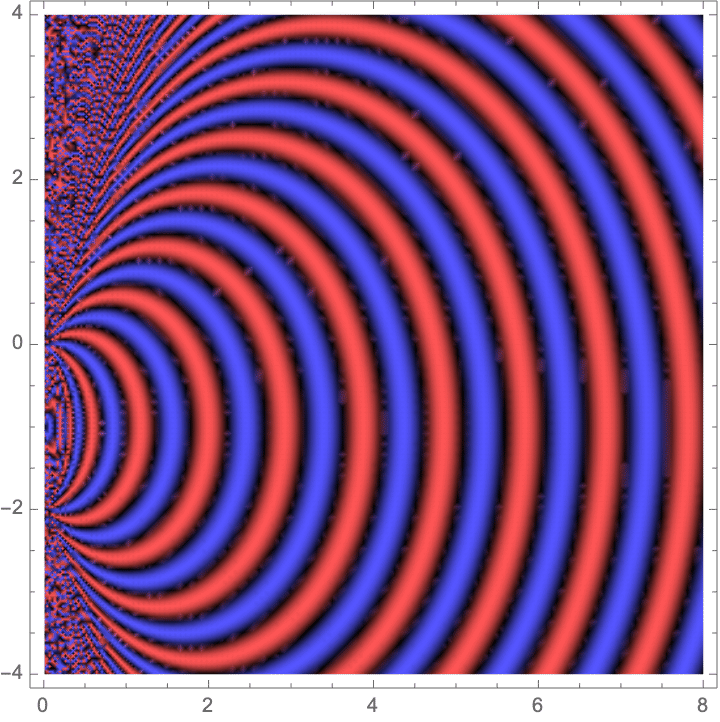
Compare this to the Fresnel kernel shifted by the same amount:
![]()
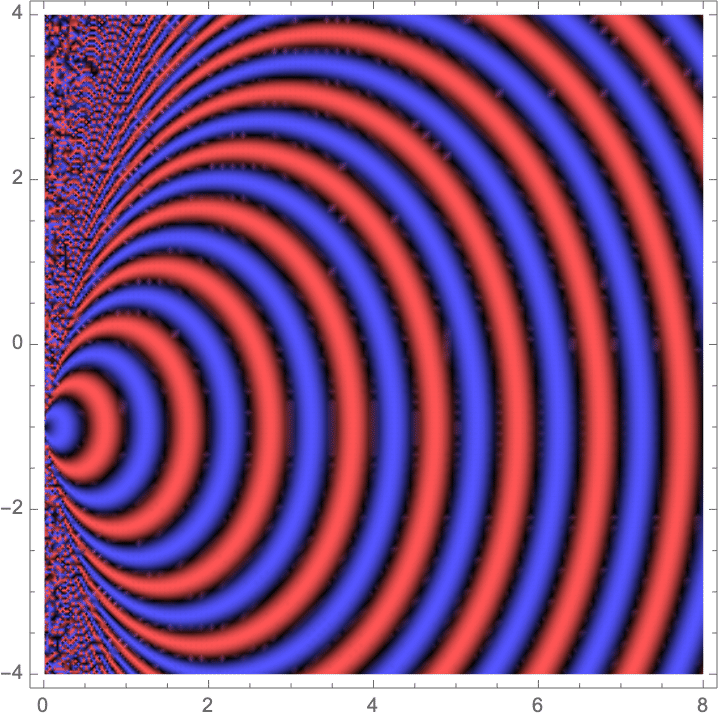
As you can see,the effect of simply multiplying by the linear phase term works really well in the far field, and only breaks down as you get too close to the source.
Fraunhofer Diffraction with Spherical Kernel
Something that never seems to be mentioned in books is that Fraunhofer diffraction is conceptually separate from Fresnel diffraction. At its core, Fraunhofer diffraction is simply a way of handling kernel shifts. It doesn't matter what we use for the static kernel in front of the linear phase term (so long as it works well within the Fraunhofer region). The paraxial approximations in Fresnel diffraction certainly lead nicely to Fraunhofer diffraction, but they are technically separate issues. Most importantly, the static kernel used will never have any interesting impact on the diffraction since it simply scales the intensity of the answer. However, if multiple diffraction patterns are to be summed, it may actually make sense to use the spherical kernel.
![]()
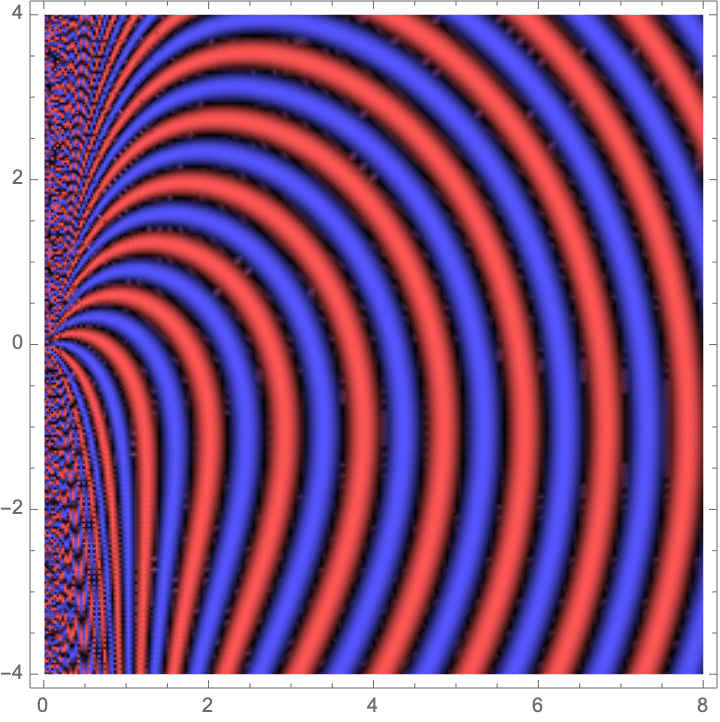
Fraunhofer Diffraction as Fourier Transform
With the Fraunhofer approximation, diffraction is treated as a linear system with an impulse response characterized by some static kernel multiplied by a complex exponential with a linear phase proportional to the shift. Since the static kernel (typically the Fresnel kernel) doesn't change with shifts, it can be moved outside of the convolution integral. So, at its heart, Fraunhofer diffraction is a linear system with a complex impulse response that is simply a complex exponential whose phase is proportional to the shift (delay) of the kernel times the distance from the origin: δ(x-Δx) → exp(i Δx α x/z), where α is some constant. A linear system is completely described by its impulse response (Green's function) so this is actually all we need to know about Fraunhofer diffraction. While not normally thought of in such terms, the fact that an impulse function in space transforms to a complex exponential (in spatial frequency) completely describes the Fourier transform as a linear operation. Thus, Fraunhofer diffraction must simply be Fourier transformation multiplied by a static function. There are obviously details I've left out like the transformation of units (you can perhaps guess from the preceding that 'frequency' in the Fourier domain will have to be proportional to x/zλ) but the fundamental operation is the same.
Finally, then, we have a useful diffraction theory since the Fourier transform is so well known analytically, and so easily computed numerically. For example, despite the seemingly intractable complexity of computing the infinite interaction of waves emanating from a finite slit aperture, anybody with a transform table (or a copy of Mathematica) can deduce that the far-field diffraction pattern of such an aperture will be very nearly sin(x)/x.
Fraunhofer Diffraction as Dispersion
Another way to look at the Fraunhofer approximation is from the perspective of dispersion. Diffraction is to spatial wave propagation as dispersion is to temporal propagation. In diffraction, spatial fourier components (plane waves at different angles) are propagated by rotating their phases by an amount that various depending on the ![]() component. In the temporal domain, a pulse is propagated by multiplying the fourier components by a phase that depends on the index of the material at a given frequency. Thus, an index that changes quadratically with temporal frequency is like diffraction (which is approximately quadratic with spatial frequency). Intuitively, if you disperse a pulse so that it's final length is much greater than its fourier limit, you basically map the frequency components to various points in time because each color experiences a different group delay. Well, this is why Fraunhofer diffraction works when you have small aperture and a large propagation distance; it's the analog of temporal dispersion of a short pulse through a large dispersive medium, except now spatial frequencies are mapped to space, in stead of temporal frequencies mapped to time. What is the operation that maps spatial frequencies to space? It's the fourier transform, with the frequency coordinate replaced by the spatial coordinate (multiplied by the appropriate scaling).
component. In the temporal domain, a pulse is propagated by multiplying the fourier components by a phase that depends on the index of the material at a given frequency. Thus, an index that changes quadratically with temporal frequency is like diffraction (which is approximately quadratic with spatial frequency). Intuitively, if you disperse a pulse so that it's final length is much greater than its fourier limit, you basically map the frequency components to various points in time because each color experiences a different group delay. Well, this is why Fraunhofer diffraction works when you have small aperture and a large propagation distance; it's the analog of temporal dispersion of a short pulse through a large dispersive medium, except now spatial frequencies are mapped to space, in stead of temporal frequencies mapped to time. What is the operation that maps spatial frequencies to space? It's the fourier transform, with the frequency coordinate replaced by the spatial coordinate (multiplied by the appropriate scaling).
Comparison of Various Approximations
What's interesting is that "Fraunhofer" diffraction with the spherical kernel is significantly better than diffraction with the fresnel kernel, especially far off-axis (where the quadratic approximation in the fresnel kernel breaks down). And yet it costs the same to compute. So, why do we use standard Fraunhofer diffraction with a fresnel kernel for cases where there is no analytic solution? (Note: since the kernel only appears in front of the integral in Fraunhofer diffraction, you might ask why it even matters, and its phase will drop out. In the case of a single aperture, it won't. But when considering multiple apertures, each of which can be computed with Fraunhofer diffraction individually, but which violates the assumption as an ensemble, the kernels will interfere and it will matter.)
To see how using the spherical kernel might improve diffraction computations in the far field (essentially for free), consider the following plot of optical phase.

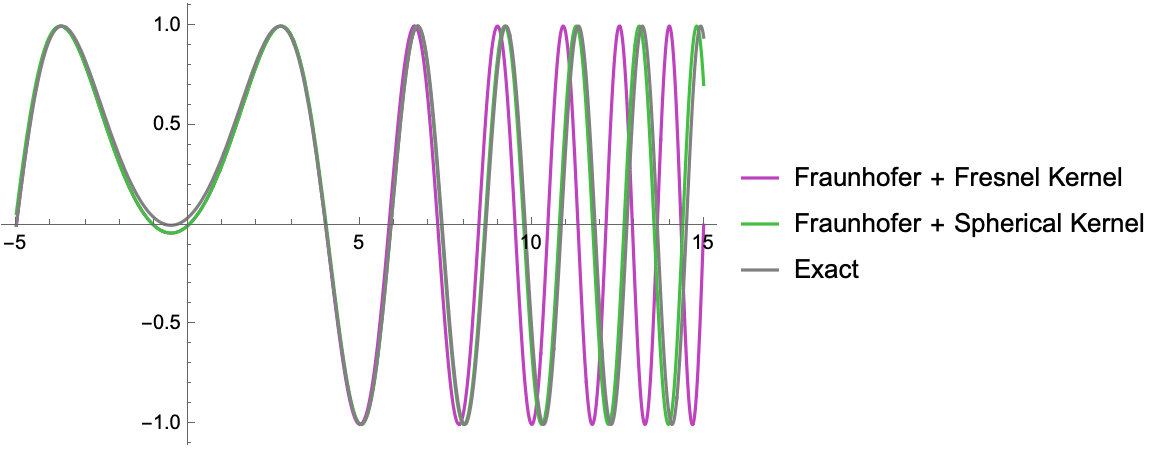
The main gist is this: relative to the exact solution (black) the Fraunhofer with the spherical kernel works much better than the fresnel approximation for large angles, even though it involves the same computational complexity.
Apodization Example
One of the things you can understand intuitively once you know that far field diffraction is just spatial fourier transformation is the “ringing” that happens when diffraction occurs from a hard edge in an aperture. The step function in space created by a hard aperture edge corresponds to high spatial frequency content. The “ringing” that you see in the far field are those high frequency terms interfering with each other. To avoid this apertures are often “apodized” which means to soften their edges so as to create a more gentle transition. Just as “windowing” in the signal processing domain is done to avoid artifacts, the same is done in optics and RF antennas.
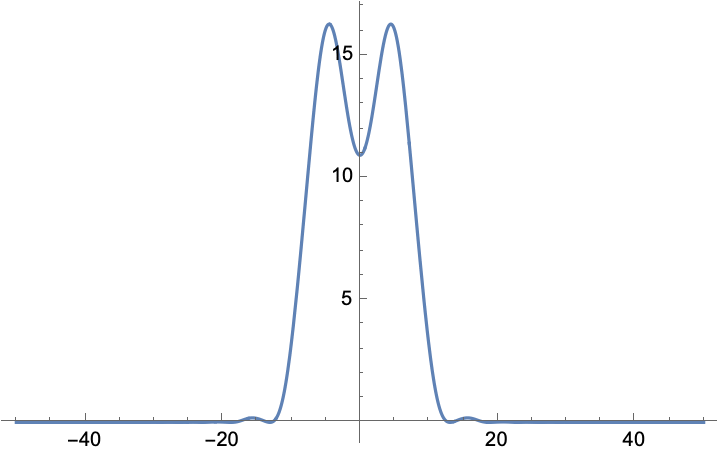
Here is an example of diffraction from a hard aperture of width 20 (in wavelength-normalized units):
![]()
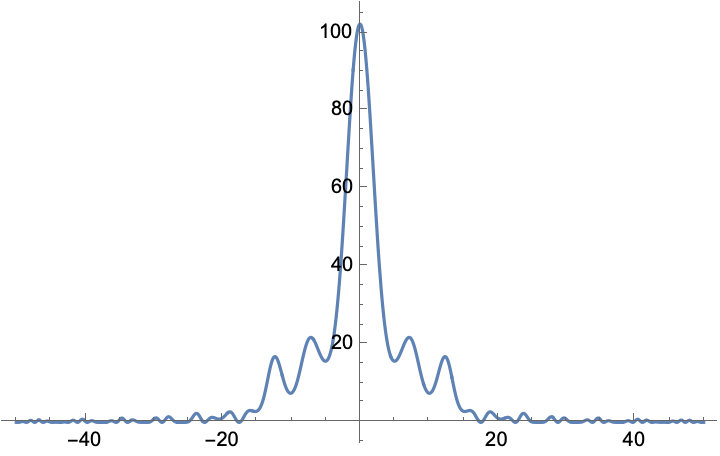
Note the “ringing” at the edges that extends considerably beyond the central peak. Now let’s consider a really simple “soft” aperture, a squared cosine:
![]()
![]()
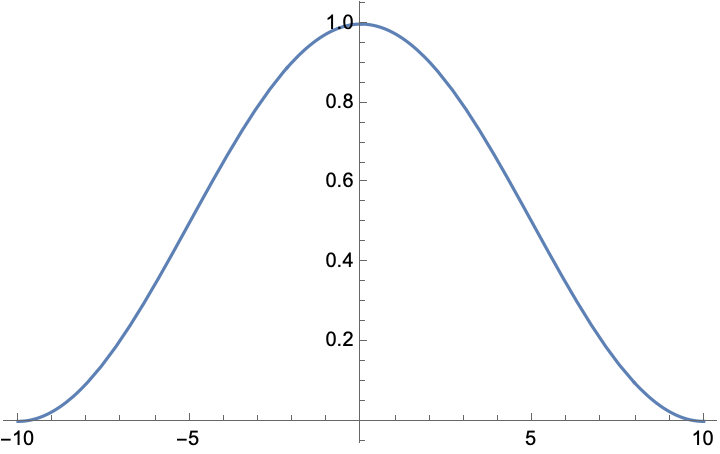
The diffraction from this aperture is, predictably, wider in terms of the central feature (as expected since we’ve effectively shrunk the aperture) but the ringing actually dies out quicker than the hard slit aperture:
![]()