Now it is your turn to do some experimenting. In order to complete this work, you will need to download Mathematica Player, which can be found here.

The physical motivation of this experiment is to think of a forest. In a very crude approximation, we can think of a forest as a lattice. There is some probability that each little square of the forest is covered by a tree. The probability of each square being covered is independent of all the other squares. In the time-honored method of physicists, we are making some very rough approximations here in order to make our problem something tractable.

Now say one of the trees is caught on fire. How will the fire spread through the forest? Will it continue to spread all the way across an enormous forest? Or, will it burn for a while, but eventually hit all of the trees around it, and then burn out? We are going to treat this problem like a percolation problem. Lets say that in each time step, a tree that is on fire will light its nearest neighbors on fire.

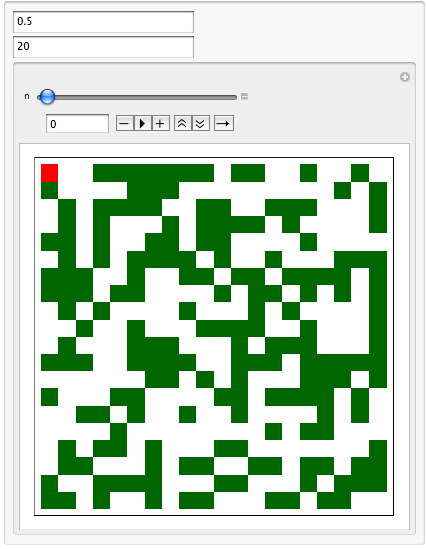
I have built an applet in Mathematica that mimics this process. It can be downloaded here. Once you have installed Mathematica Player and opened the applet, you should see:

The top of the two input boxes is the probability for the lattice. The other box is the size of the lattice. The green squares represent trees, and then red squares represent burning trees. Using the slider steps forward in time. The box under the slider tells you how many time steps you have taken.

Using different probabilities with a fixed size, see how many steps it takes for the fire to either go out or to get to the bottom of the lattice. Average over a several trials keeping the two outcomes distinct. Then, plot the average number of steps versus the probability. You can also plot the percentage of times the fire crosses the lattice as a function of probability.

When analyzing the data, you have to be careful. There are several effects going on here. Keep in mind that the lattice is not infinite, and that the tree that starts on fire is not necessarily in the largest cluster. Nevertheless, the data will show some of the interesting behavior right at the critical probability.

The idea for this experiment is from Dietrich Stauffer and Amnon Aharony Introduction to Percolation Theory