6.005 Elements of Software Construction | Spring 2011
|
The purpose of this problem set is to give you practice in using the factory design pattern and state machine modeling.
You will write factory methods to create rooms in a maze.
A maze is a collection of square rooms, each having an X and a Y coordinate. A room can have north, east, south and/or west walls. When the user first creates a maze, it has a single room at (0,0). Subsequent rooms are created by digging: the method Room dig(Room room, Direction dir) of Maze returns a new room that can be reached by going in direction dir from room. Suppose room1 has coordinates (x,y). Then
A maze should never have two rooms with the same pair of coordinates. If a maze has rooms at (x,y) and (x,y+1), calling maze.dig(maze.getRoom(x,y), NORTH) should break down the wall between the two rooms and return the existing room at (x,y+1) (likewise for the other directions, mutatis mutandis).
1. To create rooms, the generic Maze provides the method Room createRoom(int x, int y). This creates a new Room object at coordinates (x,y) and adds it to the maze. Now you would like to create a subtype of Maze with its own special rooms. Fill in the implementation of the EnchantedMaze class with a factory method to create rooms of type EnchantedRoom rather than the generic Room. [15 points]
2. Write the dig(Room, Direction) method. This method should use the createRoom method you wrote above to create rooms of the correct type. Uncomment the digging code in MazeGame's main method and verify that it produces the following easily solvable maze: [25 points]

You will write a pair of strategies for solving a maze.
One way to traverse a maze is to use the "wall-following algorithm": as you travel through the maze, keep your hand on the left wall, turning as necessary. (So, for instance, if you enter a room from the south, you take the west exit if available, otherwise the north if available, otherwise... etc.)
1. Complete the WallFollower class, an implementation of the MazeSolver interface, by adding a field to maintain the state of your maze solver---this is the direction the solver is currently facing---and implementing the visit(Room) method. [30 points]
A drawback of the above algorithm is that it is not guaranteed to get you out of any maze. If the entrance and exit to a maze are on the same wall, then the wall-following algorithm works. But, if you start off next to an inner wall of the maze, you will end up following it all the way around, and never traverse the entire maze. Indeed, consider the following small maze:
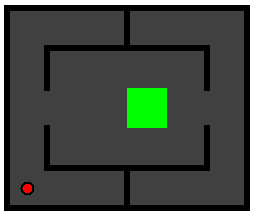
As the exit room is not next to a wall, a wall-follower will never find it. You can create this maze using Maze.makeExample2()--try stepping through it with your WallFollower strategy.
2. Complete the ImprovedSolver class with an implementation that is guaranteed to solve any maze. Here is a description, from Wikipedia, of Tremaux's algorithm, the algorithm we would like you to use to do this:
Tremaux's algorithm, invented by Charles Pierre Tremaux, is an efficient method to find the way out of a maze that requires drawing lines on the floor to mark a path, and is guaranteed to work for all mazes that have well-defined passages. A path is either unvisited, marked once or marked twice. Every time a direction is chosen it is marked by drawing a line on the floor (from junction to junction). In the beginning a random direction is chosen (if there is more than one). On arriving at a junction that has not been visited before (no other marks), pick a random direction (and mark the path). When arriving at a marked junction and if your current path is marked only once then turn around and walk back (and mark the path a second time). If this is not the case, pick the direction with the fewest marks (and mark it, as always). When you finally reach the solution, paths marked exactly once will indicate a direct way back to the start. If there is no exit, this method will take you back to the start where all paths are marked twice. In this case each path is walked down exactly twice, once in each direction.
(Find a video of the algorithm in action at http://www.youtube.com/watch?v=6OzpKm4te-E.)
Note that Tremaux's algorithm requires you to "mark" your path, keeping track of each time a room has been visited and the direction from which it was entered and exited. Do this by augmenting your solver class with a data structure containing this information. (N.B. Do not modify the Room class or other classes in package maze.) [30 points]
Note: A correct implementation of Tremaux's algorithm should efficiently complete the following example, which you can create using the method Maze.makeExample3().
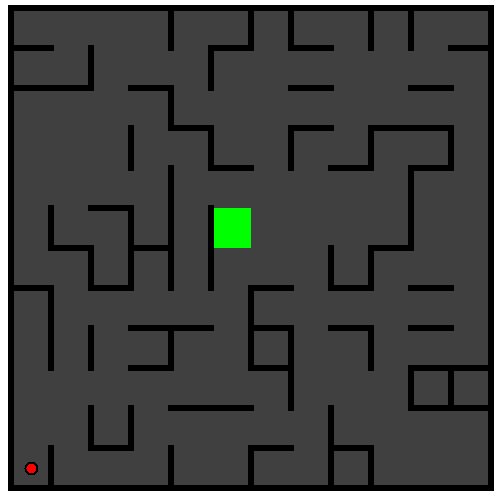
Grading for this problem set will take efficiency of your solution into account; credit will not be awarded for a strategy that takes more than 250 steps to complete this maze. (This is to keep our automated grading suite from being tied up forever.) We recommend writing a deterministic algorithm and verifying it on the above example.