6.005 Elements of Software Construction | Spring 2011
Problem Set 2: Invariants
Due: Wednesday, February 23, 2011 at 11:59pm

The purpose of this problem set is to give you practice in writing representation invariants.

Binary Search Trees

Binary Search Trees are fundamental data structures in Computer Science, and are frequently used to store a sequence of some numbers (or more generally, some “keys”) in sorted order.

You can read more about Binary Search Trees on Wikipedia: http://en.wikipedia.org/wiki/Binary_Search_Tree

The 6.006 website also has notes on Binary Search Trees: http://courses.csail.mit.edu/6.006/spring11/notes.shtml

Here are a few essential things you need to know about Binary Search Trees for this problem set:

• A Binary Search Tree consists of a bunch of “Binary Nodes”. Each Binary Node has a “key” or a number associated with it.
• A Binary Node can have at most two children: a left child and a right child. These children are also Binary Nodes, so they can each have at most two children, and so on...
• Each Binary Node in a Binary Search tree must obey the following property: the node’s key must be larger than the key for its left child, and the node’s key must be smaller than the key for its right child.
• For the purpose of this problem, a key cannot be repeated in a Binary Search Tree. Thus, there cannot be two Binary Nodes with the same key in a Binary Search Tree.

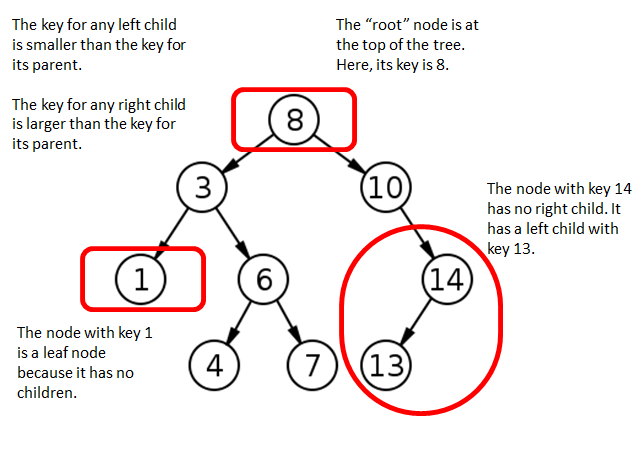
Binary Search Trees are useful because they speed up lookup of data. For example, if we want to find out whether a particular number is in a Binary Search Tree, we do not need to look through all the elements in the tree. In fact, we can get away with only looking through elements on a single path from the “root” node to a “leaf”. The number of elements on a single path from the root to a leaf is usually much less than the total number of elements in the entire Binary Search Tree.

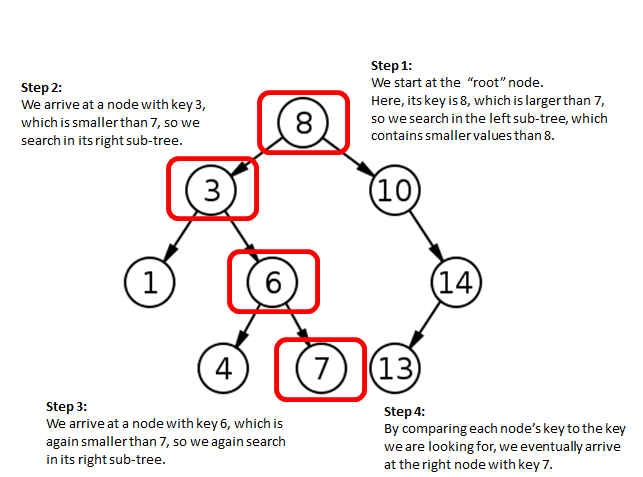
The minimum key in a Binary Search Tree is that of the left-most node (which we can reach if we keep following “Left Child” arrows). For instance, the minimum key in the example Binary Search Tree in Figure 2 is 1. Similarly, the largest key in a Binary Search Tree is that of the right-most child (which we can reach if we keep following “Right Child” arrows). In Figure 2, the maximum key is 14.

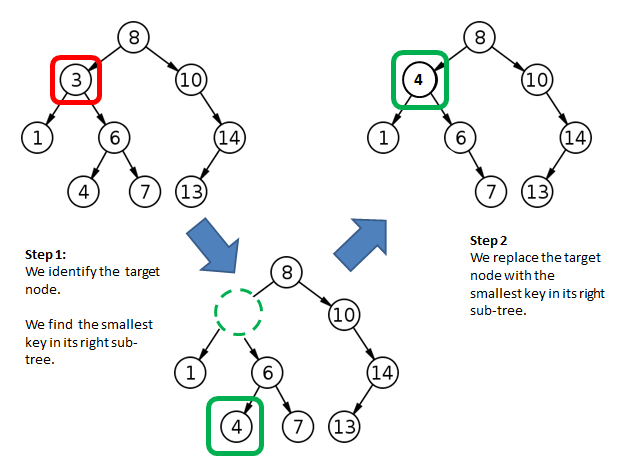
There are three cases to consider while removing node from a Binary Search Tree:

1. If the node to be deleted has zero children, then it can be simply removed from the Binary Search Tree; the node’s parent must no longer have a “Right Child” or “Left Child” pointer to it.
2. If the node to be deleted has one child, then it can simply be replaced in the Binary Search Tree by its child; the parent of the node must now point to the node’s child.
3. If the node to be deleted has two children, then it can be replaced with the minimum element in its right sub-tree. The right sub-tree is the smaller Binary Search Tree formed with the node’s right child as root. The minimum element can then be removed from the right sub-tree.

These cases are illustrated in the figures below, respectively.

Part A: Understanding Binary Search Trees [30 points]

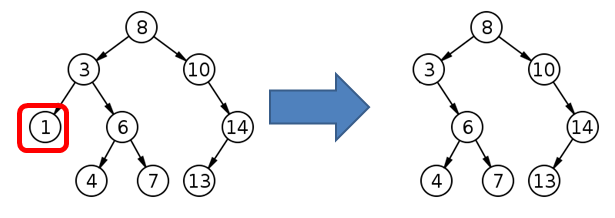
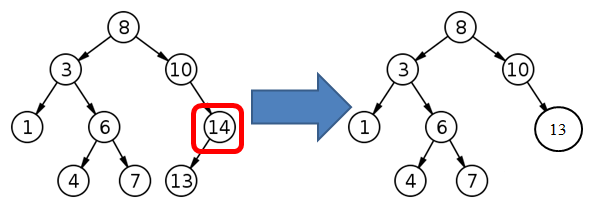
Read the source code provided in the ps2.bst_simple and ps2.bst_exception packages. Specifically, read and understand BinarySearchTree.java, BinaryNode.java, BinarySearchTreeTester.java, DuplicateItemException.java and ItemNotFoundException.java.

Tasks:

1. Write the specifications for the methods declared in BinarySearchTree.java, including annotations for @requires, @effects, @modifies, @param, @returns and @throws. Note that we have provided the specifications for all protected methods except checkRep() - you will need to provide the specifications for the rest of the methods (including checkRep()).
2. Classify all the methods in BinarySearchTree.java into constructors, producers, mutators and observers.
3. Explain the significance of the fact that both DuplicateItemException and ItemNotFoundException subclass RuntimeException. Why is this appropriate?
4. Fill in the body of the checkRep() method. Read the comments in the method carefully.
5. Add calls to checkRep() in BinarySearchTree.java. You should think about where it is appropriate to place these calls.

Once you’re done, make sure your code passes all the test cases in BinarySearchTreeTester.java.

Part B: Decoupling Binary Search Trees from the Key Type [35 points]

For this problem, only read and modify the source code provided in the ps2.bst_arbitrary_keys package.

Our current Binary Search Tree implementation is only capable of storing integers. Naturally, we would like to extend our implementation so that we can store arbitrary objects in our Binary Search Trees (such as Strings and instances of user-defined classes). In other words, we would like to decouple our code for Binary Search Trees from the specific types of objects we store in our trees as keys.

Think about how you would achieve this decoupling, before you go ahead with this problem.

A complete solution that achieves decoupling would use Generics and Java’s inbuilt Comparable<T> interface. However, considering what we have covered in the class so far, we will ignore these options and use our own interface for this purpose. This interface is defined in BinaryTreeItem.java; read and understand it.

Tasks:

1. Write the specifications for the compareTo(...) method in BinaryTreeItem.java, including annotations for @requires, @effects, @modifies, @param, @returns and @throws.

   Hint: Consider what should happen in compareTo(...) if the supplied argument is an instance of a different subclass of BinaryTreeItem? This case can be effectively specified using a combination of @requires and @throws. Reading up on Java’s ClassCastException may help.

2. Carefully read through BinarySearchTree.java and BinaryNode.java, and notice the differences from part A that were necessary to help us decouple our implementation of Binary Search Trees from the type of objects they store.

   As before, implement a checkRep() method for the modified BinarySearchTree class, and make sure to add calls to checkRep() in the right places. Also copy over the specs from part A, and modify them wherever necessary.

3. While we have defined an interface that we can use with our Binary Search Tree implementation to store arbitrary keys, existing classes in Java obviously don’t implement our interface. Thus, to get our code to store Integers and Strings, we need to write ‘wrapper’ classes that would implement our interface. A ‘wrapper’ class usually does very little itself, and exploits the implementation of some other class.

   Complete the implementation of the following classes, in order:

   • IntegerBinaryTreeItem
     The compareTo(...) method for this class should compare stored integers.

   • StringBinaryTreeItem
     The compareTo(...) method for this class should compare stored Strings.

     Consider using the compareTo(...) method already implemented by String. Read the specifications of the return value of the method very carefully. Which specification is weaker in terms of return values, the one from BinaryTreeItem or String? Which choice of return values is better, and why?

   • Student
     The compareTo(...) method for this class should order students by their String names, using the String compareTo(...) method. If two students have the exact same name, they should be ordered by their MIT ID numbers.

4. Write test cases for our decoupled Binary Search Trees with Strings and Students as keys. Test cases for Integer keys have been provided to you as a reference. Note that passing the provided test files is necessary but not sufficient in determining the correctness of your code. Add your test cases in testNormalTreeOperationsString() and testNormalTreeOperationsStudent().

Hint: Read the methods in the test suite carefully. We provide methods that you can use to generate random Strings or Students, and utility functions to find the minimum or maximum of elements in a List of any type.

Part C: Augmented Binary Search Trees [35 points]

For this problem, only modify the source code provided in the ps2.bst_augmented_abstract package.

So far, we have described and implemented Binary Search Trees with no special properties: nodes were simply sorted and arranged by key values.

Now, we will extend the functionality of our Binary Search Trees to create Augmented Search Trees. Augmented Search Trees are special types of Binary Search Trees that, apart from maintaining a sorted order of elements (based on their keys), also track some information about elements based on where these elements are stored in Binary Search Trees. We provide an abstract class for augmented search trees in AugmentedBinarySearchTree.java.

Augmented Binary Search trees have numerous applications, but we will focus on a few simple examples. For this part, you will encounter three different Augmented Binary Search trees:

• An augmented search tree that stores the number of descendants below each node.
• An augmented search tree that stores the sum of the keys of all leaves below each node.
• An augmented search tree that stores the range of node values below each node.

The first augmented search tree simply stores, at each node, the number of descendant nodes below it (excluding the node itself). This information must be dynamically updated during insertion and deletion of elements from the Binary Search Tree, without needing to visit all of the elements in the tree. A working implementation of this augmented tree is provided to you in NumberDescendantsBinarySearchTree.java. This implementation uses code from the AugmentedBinarySearchTree class, and is thus surprisingly simple.

The second augmented tree stores, at each node, the sum of the keys of all descendant leaves below it (excluding the node itself). A leaf node is defined as a node that has no descendant nodes. Note that a tree with a single node should have an augmented value of 0, since the node has no descendant leaves. This information must again be dynamically updated during insertion and deletion of elements as before, without having to visit all the elements in the tree. It will be your job to fill in code for this augmentation in LeafSumBinarySearchTree.java.

The third and final augmented tree stores, at each node, the range of values stored in the subtree containing the node (that is the difference between the max and min values). Again, this information must be dynamically updated during insertion and deletion of elements, without having to visit all the elements in the tree. Note that in this case we have given you a new class to work with, RangeBinaryNode.java, which in addition to the augmented value (representing the range) stores the value of the minimum and maximum elements in the tree. It will be your job to fill in code for this augmentation in RangeBinarySearchTree.java to update the augmented value (range), along with the minimum and maximum.

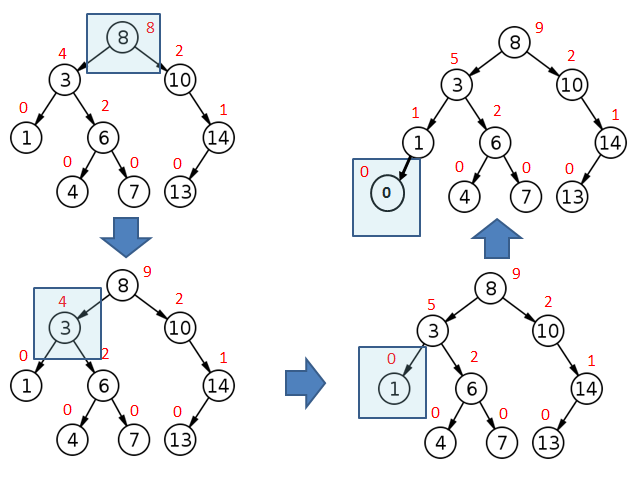
In general, there are two ways to handle augmentation. In some cases, it is possible to update information stored at each node as we walk down the pointers to a leaf or a node during insertion or deletion. Figure 4 illustrates how augmented data can be updated during an insertion.

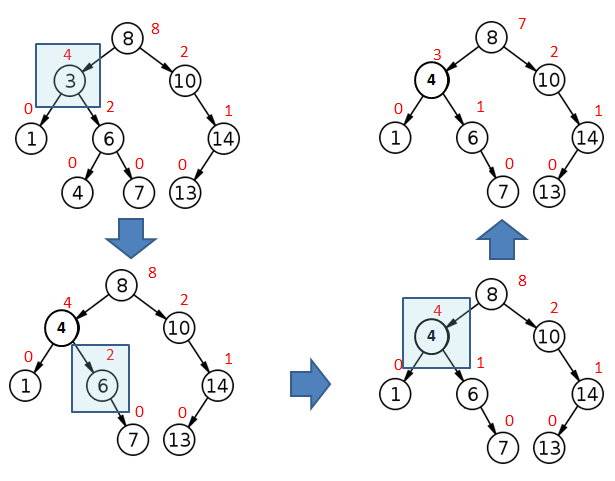
An alternative way to handle augmentation is to find the lowest element in the path along which an insertion or deletion occurred, and to propagate changes from that element upwards. This works because as long as we have accurate augmented values for a Node’s children, its own value can be easily computed, and any changes can be propagated upwards. Figure 5 illustrates an example of this for the deletion case which we saw in Figure 3c.

For this part, we provide an abstract class that handles all the described complexity associated with implementing Augmented Search trees and dynamically updating augmentation.

Read the code provided and make sure it makes sense to you, because it’s a good example of how an abstract class can provide code that handles complicated corner cases, so that a subclass only has to provide code for one/two simpler methods.

Tasks:

1. Briefly explain whether the code in AugmentedBinarySearchTree uses the “propagate upwards” approach to augmentation or whether it updates augmented values in the Binary Search Tree while walking down the tree. Why do think this is the case?
2. Read the source code for NumberDescendantsBinarySearchTree.java, and complete the implementations of the other two augmentations in LeafSumBinarySearchTree.java and RangeBinarySearchTree.java using the template for NumberDescendantsBinarySearchTree.
3. Implement the checkRep() method for each of these classes, and insert calls to it in your classes wherever appropriate.
4. Make sure that all the provided test cases pass for the three augmentations you implemented. Note that these tests may not be inclusive of all the functionality of binary search trees; thus you may want to add your own test cases. Also, the provided tests rely on your implementation of checkRep() working correctly - so if you have an incorrect checkRep() it will still be possible for the tests to pass even though your code might not be correct. (Why is this?)