First Attempts at Delaunay Triangulations
Background
This series of spherical models is a descendant of a group
of four or five solid polyhedral models.
These solid models were generated as follows:
- Pick some points on the surface of the sphere.
- For each point, take the plane tangent to the sphere, through
that point.
- Take the union of the half spaces bounded by these planes and
which includes the center of the sphere.
They were constructed of cardstock, with each face having tabs on
all its edges, folded inwards.
As well as the solid models, I had some experience with the sperical
construction methods that I'd use, from having made a couple of geodesic
domes inspired by Spherical Models by
by Magnus J. Wenninger. Those, I made while I was in highschool, using
a template drawn with a protractor and ruler, and transferred to sheets
of cover stock by pricking through both layers.
 I was concerned that polygonal cells would be unstable, when I was making
my first model, so when translating to spherical construction methods, I
looked for a way to have only triangles.
The obvious triangulation was to join each pair of generator points
whose planes share an edge.
I was concerned that polygonal cells would be unstable, when I was making
my first model, so when translating to spherical construction methods, I
looked for a way to have only triangles.
The obvious triangulation was to join each pair of generator points
whose planes share an edge.
Not yet knowing what it was called, I cheerfully set out to implement code
to find the triangulation in matlab. I got bogged down several times
while implementing it, first because I wanted to rely only on angles
between the generator points, and the trig required to do it that way
was pretty clumsy. Eventually, I had working code. It output calls to
a postscript function, and the final product was strips that would fold
into triangles.
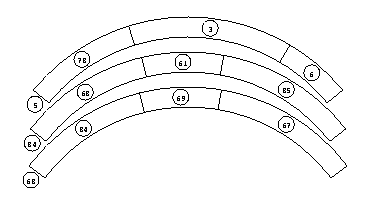
Each strip has segments of appropriate angles, and labels (on the
side that gets glued to the next one) indicating which goes where.
There's a postscript function
which takes the angles and labels as arguments, and draws the arc;
spacing between them is adjusted by hand.
The label floating off at the end is the number of that strip itself.
A tab gets cut that includes it, and it gets glued onto the other end
to close the triangle.
The full postscript is five pages,
after some hand editing to make sure pieces don't overlap or take up too much
space. To construct the model, I printed
it to lightweight cardstock on a laser printer, scored the folds with
a hard pencil, then cut and glued it; the tedious part is the cutting.

There was a detail that it took me a while to see, but which was needed
to write the code. The circumcenter of each triangle must be closer
to the three points that it's the circumcenter of, than it is to any other
generator point.
Taking these circumcenters and connecting them (edges correspond to
the edges of the triangulation, but at right angles) yields a bunch of
polygonal cells. (Corresponding to the faces of my previous solid models.)
I started to construct the model because the necessary data practically
fell out of the code, and found it to be a very satisfying and stable
model. It's less work; only three pages of postscript,
less mileage to cut and glue and no crowded junctions.
The pair of models is generated from the same 45 points, which were
picked uniformly at random over the surface of the sphere. They're about 5 1/2
inches in diameter.
Names for them
Almost a month after making the first pair of models, I was browsing
MathWorld and stumbled over
the triangulation
I'd been thinking about so much (how silly of me not to have looked earlier).
Having a name for what I was modeling not only made it a lot easier to
talk about, but I also found some java applets on the
web to illustrate the concept, and matlab built-in fuctions
to take care of a lot of the details that had initially bogged me down.
 I was concerned that polygonal cells would be unstable, when I was making
my first model, so when translating to spherical construction methods, I
looked for a way to have only triangles.
The obvious triangulation was to join each pair of generator points
whose planes share an edge.
I was concerned that polygonal cells would be unstable, when I was making
my first model, so when translating to spherical construction methods, I
looked for a way to have only triangles.
The obvious triangulation was to join each pair of generator points
whose planes share an edge.

